Оглавление:









Основные законы переноса теплоты
- В курсе»теплопередача»изучаются спонтанные необратимые процессы распределения (переноса) тепла в пространстве, где температурное поле неравномерно. Тепловые двигатели, компрессоры, холодильные агрегаты, высокоскоростные летательные аппараты, отдельные части этих агрегатов и нагреваются в процессе эксплуатации unit. In для того чтобы конструкция работала надежно, необходимо предусмотреть средства установки пределов повышения температуры.
В противном случае, когда конструкционный материал нагревается, он теряет прочность и разрушается при определенной температуре, поэтому нормальная работа таких установок может прекратиться. Например, ракетный двигатель развалится в считанные секунды, если не принять специальных мер по защите камеры сгорания и сопел входя в плотные слои атмосферы, без тепловой защиты головной части и стенок корпуса, разрушается в течение нескольких секунд.
Поскольку температура головной части достигает нескольких тысяч градусов, баллистическая ракета. Людмила Фирмаль
При работе компактного электронного устройства выделяется тепло, которое может привести к повышению температуры отдельных элементов до уровня, при котором устройство не выполняет своих функций. Ниже приведены некоторые примеры, в которых необходимо снизить интенсивность процесса теплопередачи до индивидуальной elements. At в то же время во многих других устройствах необходимо увеличивать интенсивность процесса теплопередачи.
Например, теплообменник-между 2 или более теплоносителями*, или устройство, в котором происходит обмен теплом между теплоносителем и твердым телом (стенка, сопло), будет пытаться увеличить прочность теплопередачи и уменьшить размер (стоимость материала). Все эти примеры убедительно показывают, что при проектировании тепловых двигателей, машин, самолетов и многих других устройств необходимо учитывать теплопередачу process. In в некоторых случаях эти процессы становятся решающими при выборе дизайна.
Сложные процессы теплопередачи делятся на несколько простых: теплопроводность, конвекция и теплоотдача. * Теплоноситель-движущаяся среда, которая используется для передачи тепла. Здесь и в дальнейшем мы будем объяснять терминологию, используя»рекомендуемый глоссарий», составленный Академией Наук СССР (74). Радиационный обмен. Эта техника упрощает ее study. In кроме того, каждый простой процесс теплопередачи следует своему собственному закону, как показано ниже.
Существуют молекулярные и конвективные механизмы передачи тепла. Теплообмен молекул осуществляется за счет теплового движения мелких частиц в среде с неоднородным распределением температуры. Конвективный теплообмен осуществляется в среде, в которой скорость и температура распределяются неравномерно макроскопическими элементами среды при движении. Теплопроводность-это молекулярный теплообмен в сплошной среде, обусловленный наличием градиента температуры, который выражается формулой(1-3).
Конвективная теплопередача-это процесс, в котором сочетается действие конвективной теплопередачи и молекулярной теплопередачи. Особое значение в практике машиностроения имеет частный случай этого способа теплопередачи, то есть теплообмена. Теплопередача называется конвективной теплопередачей между движущейся средой и поверхностью раздела с другой средой, включая твердое тело, жидкость или газ.
Лучистый теплообмен-это процесс, который происходит следующим образом: внутренняя энергия вещества преобразуется в лучистую энергию (энергию фотона или электромагнитной волны), излучение распространяется в пространстве (процесс переноса излучения), а лучистая энергия поглощается веществом на пути фотона. В природных объектах и инженерных сооружениях тепло передается всеми 3 способами одновременно. Этот процесс называется нагревом transfer. In во многих случаях можно выделить способ, при котором передается больше тепла.
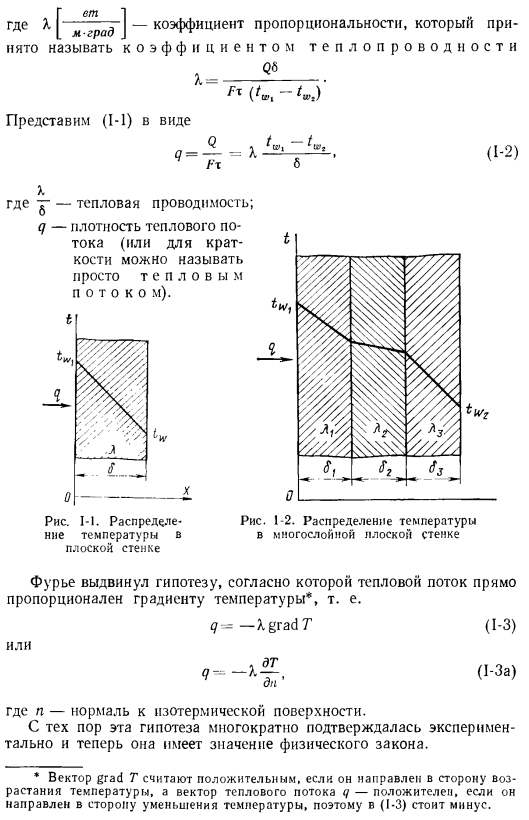
Вопрос определения его количества относительно прост. Если это не удается, задача усложняется. Теплообмен связан с очень сложным процессом, и при его изучении необходимо знать законы и методы анализа, используемые в физике, термодинамике, механике жидкости и химии. § 1.Теплопроводность Экспериментами установлено, что тепло, передаваемое плоским стенкам, прямо пропорционально разнице температур между горячим и холодным tWᵢ на стороне стенки и площади стенки F и времени t и обратно пропорционально толщине стенки 6(рис.1-1). (1-1)) 6.
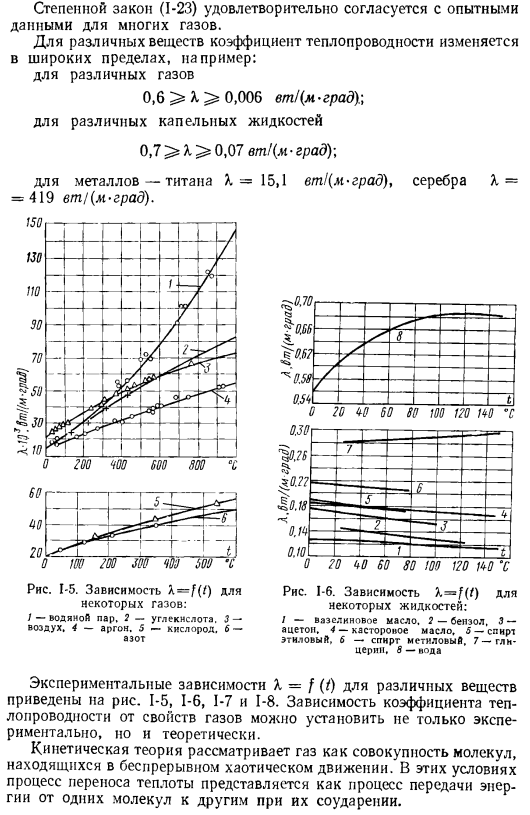
Вторник м гр-д и-коэффициент пропорциональности、 где■[% 5. назовем теплопроводность на й В6. Так… И (1-1) представляет в виде (1-2) Где y — теплопроводность. q-плотность теплового потока (или, для краткости, можно просто назвать теплым током). Рисунок 1-1.Распределение температуры плоской стены Рис. 1-2.Распределение температуры многослойной плоской стенки Фурье предположил, что тепловой поток прямо пропорционален градиенту температуры*. 7 = — x град T (1-3).
Или (1 человек на человека) Где n-Нормаль изотермической поверхности. С тех пор эта гипотеза неоднократно подтверждалась экспериментально, и теперь она имеет смысл законов физики. * Вектор gradT считается положительным, если он направлен на повышение температуры, а вектор теплового потока q-положительным, если он направлен на падение температуры. Она выражается в виде (1-2) 4.- С,-7-г — ⁽⁽⁾ Где y-тепловое сопротивление.
Определите тепловое сопротивление многослойной стены (Рис. 1-2).Напишите(1-4)на каждом слое (1-5) — ТВ, — к、 ЛЗ. Здесь и / £ — температура контактной поверхности 1-го, 2-го и 2-го слоев соответственно. (1-5) добавить в срок 62 1. 1 X, h 1 n и Из полученного уравнения видно, что тепловое сопротивление многослойной стенки равно сумме теплового сопротивления отдельных слоев. Формула для определения теплового потока через мульти-стена、 / Младший. 2 Х7-ых ⁶ ) Я, 55, 1. § 2.
Теплопередача и теплопередача Определим тепловой поток Q от жидкости при температуре tfᵢ в жидкость при температуре я / с через твердую стенку(рис. 1-3).Температура/, Г₁ и TWᵢ обычно неизвестны. Эксперименты подтвердили резкое изменение температуры жидкости тонким слоем возле стен AJ и А₂ (рис. 1-3).Этот слой называется термическим пограничным слоем. Из-за большого градиента температуры на границе происходит интенсивный теплообмен layer.
To определив тепловой поток q из уравнения (1-3), необходимо знать распределение температуры по толщине пограничного слоя, то есть функцию/ /(, v).Однако эта зависимость не является теоретической и Экспериментально сложно (Глава 7).Таким образом, Q-это часто определяется по формуле Nyogon. — / ₂ ). (В7) величина а называется теплопередачей coefficient. It характеризует прочность теплопередачи и равна плотности теплового потока q на границе раздела, называемой температурным напором (/j- / 2) между средой и поверхностью.
Уравнение (1-7), определяющее тепловой поток от жидкости к твердому телу (или наоборот), является более удобным, чем уравнение (1-3), поскольку коэффициент легче определить экспериментально, чем зависимость Г. 4, 4.、 Рис. 1-3.Распределение температуры при передаче тепла через плоскую стенку T = f(x).теоретически трудно определить коэффициент теплопередачи a (Глава 7).Продолжайте решать задачу, поставленную в начале раздела.
Настенный тепловой поток к левой поверхности (1-8) kn (рисунок 1-3) можно определить 9 = » 1(0, — «、); Через стену Программное обеспечение? = год С правой стороны стены 9 = as (α,, −0.). После простых преобразований 1-9 и 1-10)、 (1-9) (С0) формула(1-8、 (С1)) Я введу обозначения — =- Л + 4 К» 1 Л Здесь представлено суммарное тепловое сопротивление жидкого пограничного слоя на левой поверхности стенки (см. рис. 1-3), твердой стенки на правой поверхности и жидкого пограничного слоя.
- Значение (С2) Он называется коэффициентом теплопередачи. Учет теплового потока (1-12)、 //.). (1-13) Формула(1-13) не способствует выяснению физических свойств процесса теплопередачи, но полезна для практических расчетов. § 8.Теплообмен излучением Тепловой поток*при передаче тепла излучением от полностью черного объекта составляет、 =(Н4) Где AO-AO = 5.67 ″ 1о ⁻ — \ w! полная постоянная излучения абсолютно черного тела, равная mg * CN. Формула (1-14) является содержанием закона.
Стефана-Больцмана о черном теле. Тепловой поток при передаче тепла излучением от нечетного тела определяется по формуле д =ea₀ Т (1-15) Где e-экспериментально определенная blackness. It варьируется от нуля до одного. Значения е в различных веществах описаны в ссылках 147, 61 и 97. Формула (от 1 до 15) является содержанием закона Стефана-Больцмана о нечерном теле. § 4.Коэффициент вязкости Процесс передачи тепла значительно зависит от вязкости жидкости.
Давление во всех точках слоя одинакова, а пластины B движется с постоянной скоростью Wₓ. Людмила Фирмаль
Этот эффект учитывается с помощью коэффициента вязкости. Предположим, что между 2 параллельными пластинами неподвижного a и движущегося B находится жидкий слон толщиной A. (рис. 1-4).Опыт показывает, что жидкость не скользит На поверхности пластин к ним приклеиваются. Линейное распределение скорости по толщине слоя жидкости Рисунок 1-4.To вывод уравнения (Б16) (Н6) Кроме того, чтобы сдвинуть верхнюю пластину b, нужно приложить усилие в направлении движения.
Это позволяет преодолеть сопротивление движению за счет friction. As в результате сила, приложенная к верхней пластине, уравновешивает силу трения. Сила, приложенная к верхней пластине b, называется единицей ее площади и обозначается М. эксперимент, при определенных условиях Абсолютно черным телом называют тело, которое поглощает всю поступающую лучистую энергию it. At при этом такие тела излучают максимальное количество лучистой энергии при заданной температуре, по сравнению со всеми другими нечерными телами.
В природе абсолютно нет черного тела. Величина m пропорциональна соотношению WJh. In в общем случае зависимость m от распределения скорости для y имеет вид: (1-17) Здесь r. — коэффициент динамической вязкости (n-сек)/d12, являющийся физическим свойством жидкости. Формула (1-17) является содержанием закона трения Ньютона. Значение ве = — ц — (1-18) П. С. (Р-плотность вещества) называется кинематической вязкостью. Оба коэффициента guv используются в исследованиях теплопередачи.
Коэффициент динамической вязкости практически не зависит от давления, но сильно зависит от температуры(он уменьшается с повышением температуры при капании жидкостей и увеличивается с газом). Зависимость коэффициента р. от температуры газа можно выразить в виде 273-до н. э. / Т \ 3/2 Т + С (273 / ’ (1-19) Где U-коэффициент вязкости при t = 273°. С — — — Сазерленд постоянной.
Р различных газов. значения для o и C приведены в таблице. 1-1 [15]. Таблица 1-1 Наименование газа ЕД-I01, (Н-сек / м) с Воздух…………….. 1,71 117 Аргон……………… 2.10 170. Азот……………… 1,70 111. Водяной пар…………… 0.92 650 Данные приведены в таблице. 1-1, полученные экспериментально. Описаны экспериментальные значения коэффициентов вязкости для различных жидкостей (47, 971. Зависимость коэффициента вязкости р от свойств газов может быть установлена не только экспериментально, но и с помощью кинетической теории газов[16, 76].
Идеализированный газ состоит из молекул. Молекула считается абсолютно жестким шаром с диаметром d.Масса / p, средняя скорость и; газ находится в сосуде * Предопределяет характер взаимодействий между молекулами, делая их полностью твердыми и attractive. In в случае общего взаимодействия диаметр d понимается как расстояние, на котором молекулы могут приближаться друг к другу в среднем[76]. В линейных размерах L число молекул на единицу объема равно n. среднее значение среднего свободного пробега молекул между столкновениями выражается как/, А 1) Z> dn 2) L ^> 1.
При выполнении условия(1) молекулы движутся преимущественно по прямой линии, и парные столкновения между молекулами преобладают. Условию (2) соответствует среднее давление газа, когда каждая молекула, проходя через газ, сталкивается со многими другими молекулами в своем path. In в этом случае двойное столкновение молекул играет важную роль. Во многих практических задачах газ находится в состоянии, когда выполняются условия (1) и (2).
Предполагая преимущественно двойное столкновение с одноатомным газом и отсутствие более сложных столкновений, мы можем найти зависимость между коэффициентом вязкости p и величиной плотности газа p, средней молекулярной скоростью v, средним свободным путем / молекул и т. д. | 1 = 3-ры. (1-20) Формула(1-20) была впервые оценена Максвеллом. Для средней скорости перемещения молекулы формула Где k = 1.38-10-23j / град-постоянная Больцмана. Для среднего свободного пробега молекулы, формула 7 = — (1-22) версии v2.Т(ф-Н Используя кинетическую теорию газов, был разработан приближенный метод определения коэффициента вязкости Р смеси газов (16, 27). § 5.
Коэффициент теплопроводности Обычно коэффициент теплопроводности х (1-1) определяется экспериментально. Величина х зависит от физических свойств и температуры вещества, а также от давления в случае газа и пара. Температурная зависимость теплопроводности газов может быть выражена следующим образом (В23) Где 1 — теплопроводность при температуре T = 273°. Степенной закон (1-23) полностью согласуется с экспериментальными данными многих газов.
Для разных веществ теплопроводность существенно отличается. Например、 Для различных газов 0.6 > X> 0.006 W /(M-степень); Для различных инфузионных растворов 0.7 > x> 0.07 Вт1(М * Град); Для металлов-титана X = 15,1 Вт (степень), серебра X — = 419 Вт /(степень м) Рисунок 1-5.Зависимость некоторых газов A = f(/): / _ Водяной пар. 2-углекислый газ. 3-воздух. 4-аргон, 5-кислород, б-азот Рис. 1-6.Зависимость некоторых жидкостей X = f(/): 1-Жидкий Парафин. 2-бензол,3-ацетон, 4-касторовое масло. 5-этиловый спирт, 6-метиловый спирт, 7-глицерин, 8-вода .
На рисунке показана экспериментальная зависимость различных веществ: X = f (/). 1-5, 1-6, 1-7 и 1-8.Зависимость теплопроводности от свойств газов может быть установлена не только экспериментально, но и теоретически. Кинетическая теория рассматривает газ как совокупность молекул, находящихся в непрерывном хаотическом движении. В этих условиях процесс теплопередачи представляется как процесс передачи энергии от одной молекулы к другой при столкновении.
В кинетической теории газа получена следующая зависимость от коэффициента теплопроводности: (1-24) Где i-безразмерная постоянная. Для одноатомного газа i = y, для многоатомного газа i—(9 / g-5)^здесь k — ^ 7); Cv, s’P, — молярная теплоемкость газа в процессе при постоянном объеме и давлении. Рис. 1-7.Зависимость некоторых металлов X = [(/): 1-чистая медь, 2-медь 99,9%. 3-алюминий 99,7%, 4-алюминий 99,0%, 5-чистый марганец. 6-99. 6% марганца. 7-СК 99,8%, 8-Чистая Платина. 9-никель 99% 10-никель 97%, / / — железо 99,2%. 12-Sziket технически чистый Рис. 1-8.
Зависимость некоторых строительных материалов и теплоизоляции X = f ( / ): / — воздух. 2-минеральная вата,3-шлаковый каркас,4-ньювел, 5-совелит, 6-диатомовый кирпич. 7-красный кирпич, 8-шлакобетонный кирпич, 9-шамотный кирпич Для одноатомных газов формула (1-24) может быть отображена в удобном виде фактическим calculations. To сделайте это, замените теплоемкость (1-24) (Где D-универсальная газовая постоянная) И когда (1-20) предоставляется、 Х т-т’3i ⁵2⁵) Из Формулы (1-25) видно, что вязкость и теплопроводность идеализированного газа (§ 4) взаимосвязаны. Используя кинетическую теорию газа, был разработан приближенный метод определения теплопроводности х газовых смесей 116, 271. § 6.
Коэффициент теплопередачи Для определения теплового потока по формуле Ньютона (1-7) необходимо знать значение коэффициента теплопередачи a. It изменяется в широких пределах, в зависимости от условий, в которых происходит теплообмен и физических свойств жидкости, которая очищает твердое тело. Например, коэффициент теплопередачи нагревательной батареи для воздуха в помещении составляет около 17 Вт / (м2 градуса), а воздушная поверхность баллистического снаряда при входе в плотную атмосферу составляет 1700 Вт /(I2 градуса), то есть более чем в 100 раз.
Коэффициент теплопередачи воды на внутренней поверхности нагревательной батареи составляет около 3500 Вт! (2-град), а конденсация водяного пара на твердой поверхности может достигать 12 000 Вт! (2-град). Лишь в редких случаях удается определить коэффициент теплопередачи теоретически(Глава VII). как правило, он определяется экспериментально, а результаты в виде таблиц, графиков или эмпирических зависимостей рассматриваются в литературе[10、15、45、47、51、61、[97, например]. Как определить коэффициент теплопередачи a для различных условий теплопередачи обсуждается в разделе 2. VII, VI11, IX, X, XI, X11.
Смотрите также:
| Основы энерготехнологии | Основные дифференциальные уравнения теплообмена |
| Вторичные энергетические ресурсы | Метод обобщенных переменных |

