Внецентренная нагрузка короткой стойки

Внецентренная нагрузка короткой стойки

Эксцентриковая нагрузка короткого стеллажа Эксцентриковая нагрузка-это особый случай растягивающего или сжимающего напряжения из-за напряжения изгиба. Если длина стержня не очень велика по сравнению с поперечными размерами, то его прогиб настолько мал, что им можно пренебречь Нм по сравнению с исходным эксцентриситетом Е\, поэтому можно использовать принцип сложения*действия.

• Например, рассмотрим случай сжатия продольной силой P с эксцентриком e (рис. 224), приложенным к одной из 2 главных осей сечения. При приложении 2 равных противодействующих сил Р При поперечном сечении в центре тяжести это условие не изменяется, так как оно равно нулю.

Затем, Б) получают осевое сжатие силой P. Это вызывает перпендикулярное напряжение — (ReuCr), как показано на рис.8, напряжение сжатия непосредственно-P \ p 224, Б и рис. 2. пара усилий Пэ, ПК и гнуть на 1 главной плоскости. 224, стр. В результате общее напряжение Рисунок 224. ■- 4 — ^ — с） Окей.

На рисунке показано распределение суммарного напряжения. 224, A. 224, и максимальное напряжение из-за изгиба предполагается меньше осевого напряжения сжатия, поэтому только 1 напряжение сжатия вдоль всего стержня Поперечное сечение натяжения. Если максимальное напряжение изгиба больше, чем прямое напряжение сжатия, линия нулевого напряжения параллельна оси z, сечение разделено на 2 зоны, растягивающее напряжение приложено слева, а сжимающее напряжение приложено справа. 

Для прямоугольного поперечного сечения со стороной ступицы(рис. 224,а) формула (А)имеет вид: Р 12 Лей ЧД. (ля’ ） bh9. И получим подстановку y =- (I / 2) v _ _ _ R. 6 футов? _ （ <си> Значения i0 * /™ * — БХ » Р БГ-БГ г * ) Для эксцентриковых нагрузок на длинных стержнях см.§ 56. если мы назначим y = L2、 Р б вновь (с） Б \ ХД Да. e в случае L / 6 знак напряжения изменяется, и положение нулевой линии напряжения получается путем приравнивания общей формулы oh (a ’)к нулю.

И затем… Л2. \ 2е (<*） Или используйте/для вычисления инерционного радиуса вокруг оси 2(см. Приложение） У4. (134） Можно видеть, что расстояние O линии нулевого напряжения от 4 минут 1 силы тяжести уменьшается с увеличением эксцентриситета e. то же рассуждение может быть применено и в случае эксцентричной растягивающей нагрузки.

Если точка приложения нагрузки находится в 1 точке на главной оси инерции, то формула (134) может быть применена и к другим формам поперечного сечения. Теперь рассмотрим случай, когда приложенная точка B эксцентриковой силы сжатия P не находится ни в одной из 2 главных осей инерции поперечного сечения, взятого на Рис.2. для оси y и оси r 225.

Если в качестве координат этой точки взять m и n, то момент P силы на осях y и r равен соответственно Pn и Pm. Используя принцип сложения действия силы, вы получаете напряжение в определенной точке. LҐN ’ ■ / ч / ч / ч т Н-У Р 0 ч н \ ч р ^ В \ Ш 4/1 3 часа/ ’ М. Л. // В. Рисунок 225.

Оказывается, распределение напряжений подчиняется линейному закону. Людмила Фирмаль

Первый элемент справа представляет напряжение сжатия, а другие 2 представляют напряжение изгиба, вызванное моментами Pm и Pn соответственно. Формула для нулевой линии напряжения получается путем приравнивания правой части Формулы (Е) к нулю. Используйте обозначения И/ y / H=/£, где/,, и 1y-соответствующие инерционные радиусы для осей r и y、 ^ + л4-н = о (Д） Подставляя в это уравнение y = 0, а затем 2 = 0, получаем точку M•I N — точку пересечения нулевой линии напряжений с координатными осями r и y (рис.225).

Координаты этих точек 5 и R северный= — И N * 4 ’»’ » ■гг *. Б * Т= -• -. Г. < 0 «Где найти Поскольку эти уравнения имеют тот же вид, что и уравнение ( £ ), если в точке 5 приложена нагрузка с координатами 5 и r, то соответствующей нулевой линией будет линия LGL,»обозначенная пунктиром n на рисунке»отсечка, ось y и сегменты g тип.

Точка приложения B нагрузки (положение соответствующей нулевой линии)} существует еще одно важное соотношение между напряжением. То есть, если B движется вдоль линии HOL (рис.226), то соответствующая нулевая линия напряжения вращается вокруг определенной точки B. 

Об этом свидетельствует: разбейте нагрузку на 2 параллельные составляющие.1 — Bx, еще 1-B%. Поскольку компонент Bx действует в главной плоскости x1, то соответствующая нулевая линия напряжений параллельна оси y, а ее отрезки на Og, kai определяется из Формулы (134) и формулы аналогично-равно 1. (Си）

Аналогично, линия нулевого напряжения компонента Br параллельна оси z, а расстояние от этой оси равно (Ч т. В определенном положении нагрузки на линии BXBY, напряжение тока нул на B.So, когда точка приложения нагрузки перемещается вдоль призмы BXB, соответствующая нулевая линия напряжения вращается около 4 точек B, координаты которых определяются формулами (b) и (1).

• Задачи 1.Сечение площади стержня уменьшается вдвое по ТП(рис. 227).Определить максимальное растягивающее напряжение поперечного сечения TP, вызванное продольной нагрузкой P < 。 2Р Ра 24 8я Ответ. (О) Макс — £ * ±4 * а » = = а * 2.Решите предыдущую задачу, предположив, что поперечное сечение стержня является круглым. — 3.

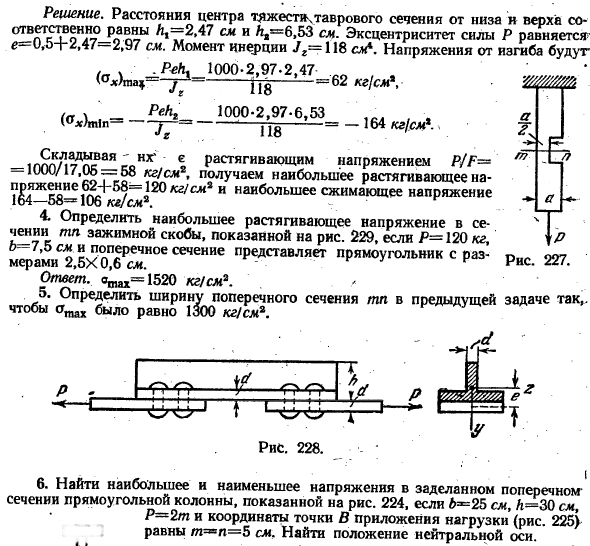
Нагрузите эксцентрик р на стержень Т-образного сечения (рис.228).Определите максимальные растягивающие и сжимающие напряжения для этого стержня.«Ель см, L-9 см, ширина полки L = 9 см, P = 1000 кг. Решение. Расстояние центра тяжести Т-образного сечения снизу вверх составляет L = 2,47 см и L = 6,53 см соответственно, а эксцентриситет силы P равен e = 0,5 + 2,47 = 2,97 см.

Момент инерции 7g = 118 сек. Людмила Фирмаль

Напряжение на изгиб составляет HX-e P / / r =складно-растягивающее напряжение = 1000/17. 06 = 58 кг / см2, максимальное растягивающее напряжение 62 + 58 = 120 кг / см2 и максимальное сжимающее напряжение 1-4 = 106 кг! См2. Определите наибольшее растягивающее напряжение на поперечном сечении TP зажимного кронштейна, показанного на фиг. 4. 229(для Р = 120 кг） 6 = 7,5 см, поперечное сечение 227 размер прямоугольника и 2. 5×0. 6 см. Ответ. Максимум= 1520 кг / см2. »

Определите ширину поперечного сечения mn предыдущей задачи так, чтобы atax составлял 1300 кг / см2. Часы работы. PrHx 1000-2. 97-2. 47 -. ЦО, л (пр) ша,= ^ л = у = 62 кг) см 1000-2. 97-6. Пятьдесят три 118. 77. 6.Найдите максимальное и минимальное напряжения в неподвижном поперечном сечении квадратного столба, показанного на рисунке. Найти положение нейтральной оси, где 224, 6 = 25 см, L = 30 см, P-2m и координаты точки B нагрузки (рис.225) равны m =»l = 5 см. 4. Рисунок 228. К Ногу вверх. ^ 7 = Но… −164 кг / см *. (^®х) m1n = Так… ％

Смотрите также:

Предмет сопротивление материалов: сопромат

Ядро сечения	Изгиб балок в главной плоскости, которая не является плоскостью симметрии
Внецентренное сжатие гибкой симметричной колонны	Изгиб, сопровождаемый растяжением или сжатием