Оглавление:





Изгиб балок в главной плоскости, которая не является плоскостью симметрии
Искривление луча на главных плоскостях, которые не являются симметричными При рассмотрении чистого изгиба в центре сдвига (см. стр. 195) было показано, что плоскость изогнутой оси совпадает с плоскостью пары изгибов. Однако эти пары действуют на одном из 2 основных изгибов planes. In в случае изгиба балки за счет поперечной силы со-плоскостной системы задача усложняется.
- Если основная поверхность, на которую действует сила, не является плоскостью симметрии балки, то такой изгиб обычно сопровождается закруткой балки. Следующая презентация показывает, как этот поворот может быть удален и простой изгиб может быть получен путем правильного перемещения плоскости силы, действующей параллельно себе. в.
Начнем с простого примера, где поперечное сечение балки имеет 1 ось симметрии (ось g) и сила действует на плоскость, перпендикулярную этой оси (рис.208).Рассмотрим случай тонкостенных балок, как показано на рисунке. Предыдущее обсуждение распределения вертикальных касательных напряжений xxu(p. It можно сделать вывод, что почти все боковые силы Q воспринимаются только с 1 выступа, из числа (см. 110).
Если рассматривать полки как 2 отдельные балки, и в их поперечном сечении соответственно присутствуют моменты инерции Y ’и Y», то кривизна и прогиб при изгибе будут одинаковыми, если*распределить между ними относительно J, g: J, g1.Тогда боковые силы этих полков будут находиться в таком же соотношении.
Это условие выполняется, когда боковая нагрузка действует на вертикальную плоскость, проходящую через точки O (рис.208, а). кроме того, Hx:/ y = Y «:Y’. Людмила Фирмаль
Таким образом, можно видеть, что точка о перемещается от центра тяжести поперечного сечения с к полке, где Момент инерции поперечного сечения равен large. As показанная в Б на фиг. 208, если одна из полок отсутствует, то это та часть полки, которая предполагает с достаточной точностью, что точка о совпадает с центром, и для того, чтобы получить простой изгиб, необходимо, чтобы поперечная нагрузка действовала на вертикальную поверхность, проходящую через эту точку.
Далее рассмотрим поперечное сечение канала(рис. 208, В) и определим Положение плоскости, в которой действует перпендикулярная нагрузка, создает простой изгиб, в котором нейтральная ось совпадает с осью Z. Для этого необходимо учитывать распределение касательных напряжений по сечению для простых bending.
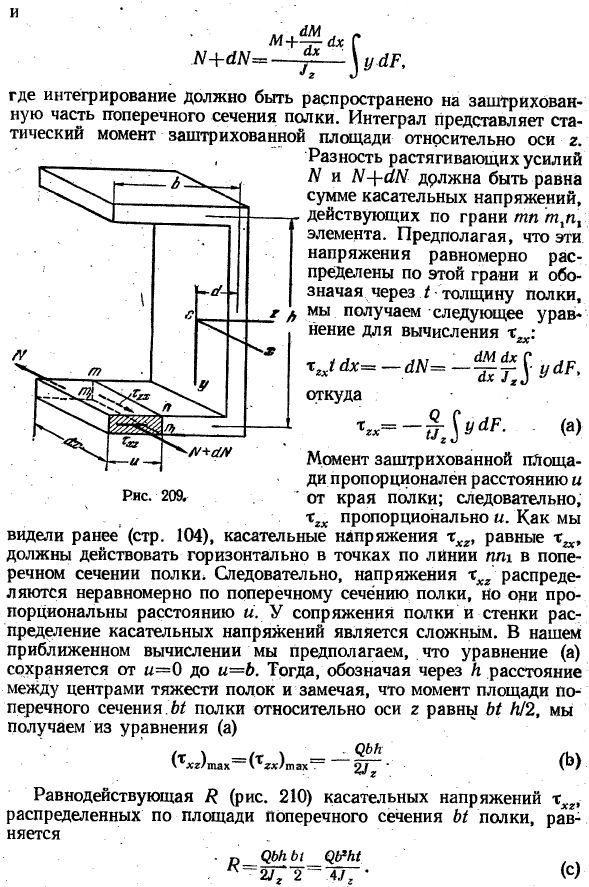
To рассчитать вертикальное тангенциальное напряжение xxx поперечного сечения стенки можно тем же методом, что и для двутавровой балки (p. горизонтальное тангенциальное напряжение появляется на shelf. To определив величину этих напряжений, рассмотрим элементы, отрезанные от полки двумя смежными участками на расстоянии c1x и в вертикальной плоскости t. nn ^параллельных стенок(рис. 209).
- При изгибе балки вниз нижний фланец растягивается, и напряжения N и L — > — L, действующие на вышеуказанные элементы, равны. Бл * * * + — * х — Тангенс. Н + дн = LR. Уплотнение должно распространяться на затененную часть поперечного сечения полки. Интеграл представляет собой статический момент заштрихованной области относительно оси Z. Разность напряжений N и L + M должна быть равна сумме касательных напряжений, действующих вдоль плоскости mn элемента.
Если предположить, что эти напряжения равномерно распределены по этой плоскости и представлены толщиной полки, то получается следующее уравнение: ХХХ ((1х = — dу Откуда? Х расчет гормон роста’ Моховой. ГАУ’Ч’- икс х ’ * = — ГГТ $ какая- (ля) Момент штриховки dH пропорционален расстоянию, рис. 209.С края полки.
Когда полки и стены выровнены, распределение напряжения сдвига является сложным. Для приближенного расчета предположим, что уравнение (a)записано от u = 0 до u = B. Затем обозначим расстояние между центроидами полки на Λ и отметим, что момент поперечного сеченияackspacks относительно оси z равен Л/ / 2, полученный из Формулы (a (Ушх =(Тгх) Шах = — 5Т * — о «) Результат/? (Рис. 210), тангенциальное напряжение xxg, распределенное по площади поперечного сечения фланца S, равно Достаточно Р (С) 2-4У.、
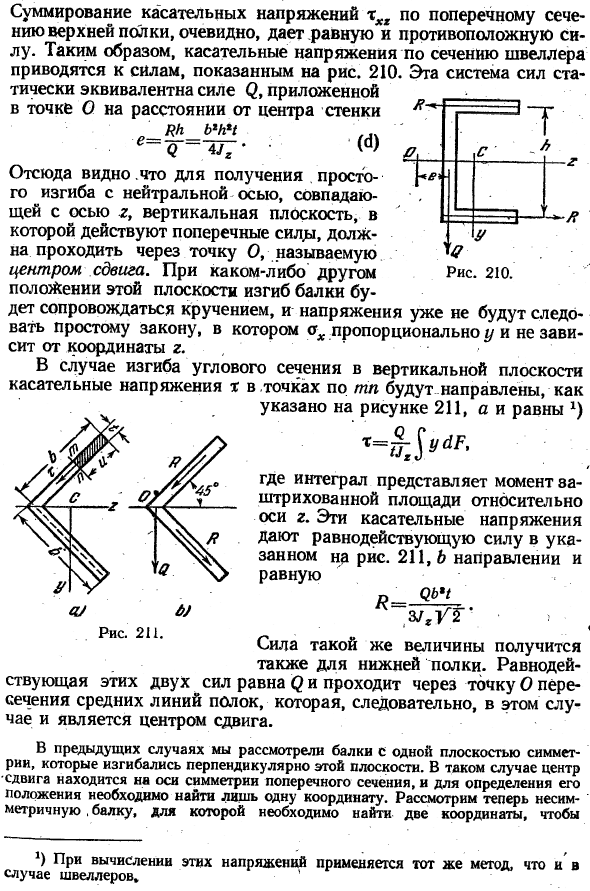
Сумма касательных напряжений xxx по поперечному сечению верхнего фланца, по-видимому, дает равные и противоположные силы. Таким образом, тангенциальное напряжение поперек сечения канала уменьшается до силы, показанной на Рис.1. 210.Эта система сил эквивалентна силе 0, приложенной в точке О вдали от центра стены и статической ’/?Один с = о — = rm7-•(<1)
Следовательно、 xx пропорциональна and. As как было показано ранее (стр. 104), касательные напряжения xx, y равны m ^и должны действовать горизонтально в точках вдоль линии rm поперечного сечения. Людмила Фирмаль
Это означает, что вертикальная плоскость, на которую воздействует боковой порог, должна проходить через точку O для получения простого изгиба с нейтральной осью, совпадающей с осью 7.Центр сдвига. С друзьями!»Положение этой плоскости, изгиб балки сопровождается кручением, а напряжение не подчиняется простому закону, что oX пропорционально y и не зависит от координаты r. В случае изгиба углов вертикальной плоскости тангенциальное напряжение x в точке вдоль TP направлено следующим образом:
Он показан на рисунке 211, равен а*) а / 6.) Рисунок 211. Здесь Интеграл представляет момент заштрихованной области относительно оси z эти тангенциальные напряжения дают результирующие силы в направлении, показанном на рисунке. 211, B направление и равный N мяч. ля. / ЕДИНОЕ ВРЕМЯ. • Такое же усилие получается и на нижних полках.
Равнодействующая сила этих 2 сил равна φ и проходит через точку пересечения O центральной линии полки. Поэтому в данном случае, это центр сдвига. В предыдущем случае мы рассматривали балку с 1 плоскостью симметрии, изогнутой перпендикулярно этой плоскости plane. In в этом случае центр сдвига находится на оси симметрии поперечного сечения, и для определения его положения необходимо найти только 1 координату.
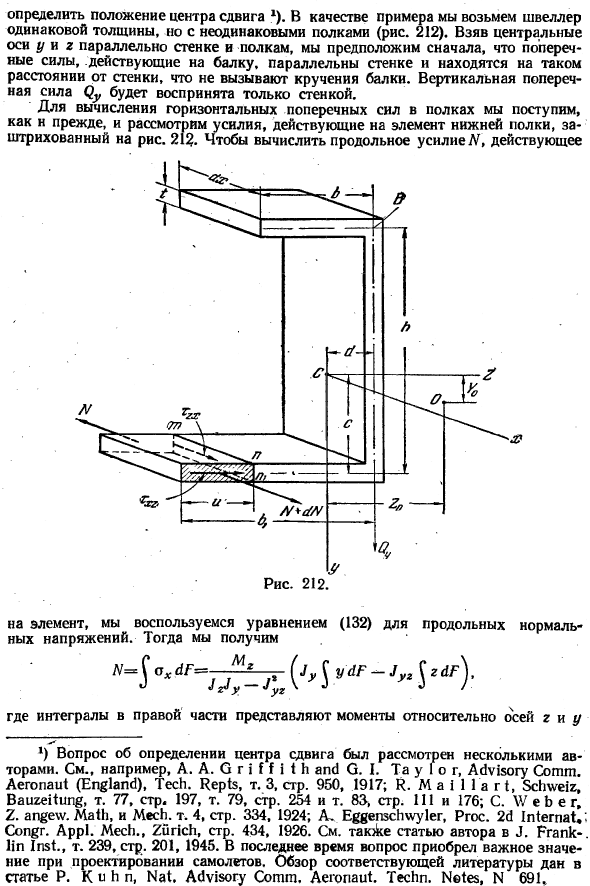
Теперь рассмотрим asymmetry. In для того, чтобы луч вам нужно найти 2 координаты ’ •/ * ) При расчете этих напряжений используется тот же метод, что и для канала. Определите положение центра сдвига*). в качестве примера возьмем канал с разными полками одинаковой толщины(рис. 212).
Если мы возьмем центральные оси y и g параллельно стенам и полкам, то прежде всего будем считать, что боковые силы, действующие на балки, параллельны стенам и не вызывают скручивания балок на расстоянии от стен. Вертикальная сила сдвига (} воспринимается только стеной.
Для того чтобы рассчитать горизонтальные боковые силы полок, действуйте так же, как и раньше, и учитывайте силы, действующие на элементы нижних полок с тенями фигуры. 21?。Для расчета вертикальной силы # действие Для каждого элемента используйте уравнение (132) для продольного нормального напряжения. И затем… Где Интеграл справа представляет момент для осей r и y 1) вопрос определения центра сдвига рассматривался несколькими авторами.
Например, А. А. Гриффитс и Г. И… Ta y 1 O g, пожалуйста, обратитесь к консультативной связи. Аэронавт (Англия), Тех. Лептос, т. к. 3, p. s. 950, 1917; R. M a 1 1 1 a d t, Schweiz, Bauzeitung, t. to. 77, стр. 197, ст. 79, стр. 254 и ст. 83, стр. 111 и 176; С. В / Е Б Е Г, З. angew. Математика и я. т. к.4, p. s. 334, 1924; A. Eggen Schwarz, Proc. 2Д интернат * поздравления с днем.
Применение Мех., Цюрих, 434, 1926.J. Franklin Inst., T. 239, p. см. также статью 201, 1945 автор. В последнее время этот вопрос приобрел все большее значение при проектировании самолетов. Обзоры соответствующей литературы можно найти в журнале INR. K и h N, Nat, как описано в статье в консультативной связи. Летчики.
Технические Примечания, N 691 действует на плоскости, параллельной плоскости XY. Уравнение (133) используется для расчета нормального напряжения ah. Снова глядя на теневой элемент 212 риса и ведя себя как раньше и、 1 ^ 17 ^УУГС, и & + и’»]’ Горизонтальная тангенциальная сила Нижнего фланца равен Г-Я, б[‘ГВе (А6,\ — | 2-’(2 часа)} Возьмем момент действия этой силы на точку B (рис. 212) и горизонтальную тангенциальную силу (?).
Чтобы получить расстояние / плоскость рабочей силы от точки B, делим на (вызванное внешней силой).Тогда нужная координата центра сдвига будет-Л==. = = с Эй. \ * л.£- у ’(*іі 1 * 2 ’ * * <2 зл У » ГУ В особых случаях равных полок ч я c = = — 2 и выражается цифрами(1 и 1y>могут быть указаны.
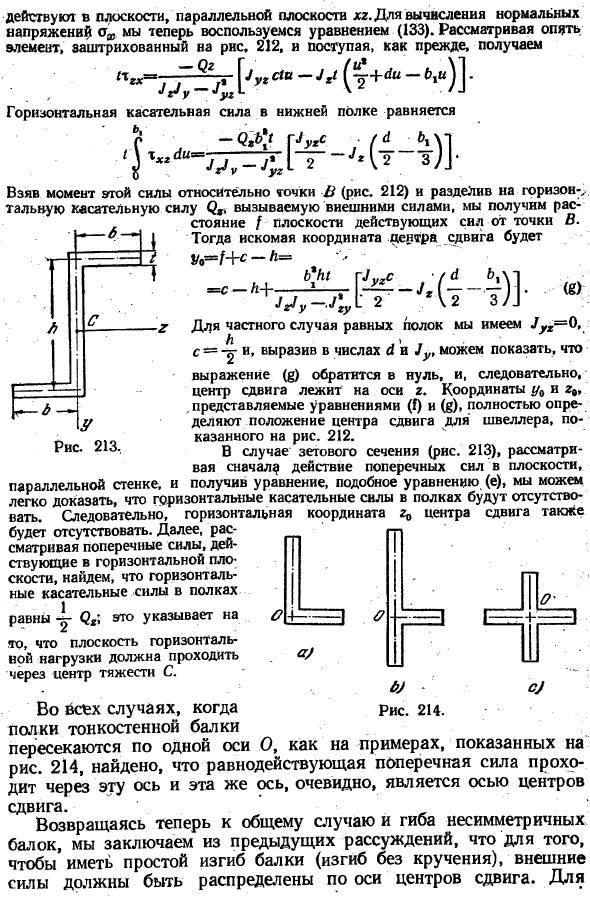
Уравнение исчезает, и поэтому центр сдвига находится на оси 2.Координаты y0 и rv, представленные уравнениями (0 и^), полностью определяют положение центра сдвига канала, показанного на рисунке. 212. В случае Дзета-сечения (рис.213) можно легко доказать отсутствие горизонтальной тангенциальной силы на полке, сначала рассмотрев действие боковой силы в плоскости, параллельной стенке, а затем получив уравнение, аналогичное уравнению (е).
Поэтому также отсутствует горизонтальная координата сдвига Center. In кроме того, если учесть боковые силы, действующие на горизонтальную плоскость, то горизонтальные тангенциальные силы полок составляют когда Равно 4 -; это указывает Б) * рис 214.
Плоскость горизонтальной нагрузки должна проходить через центроид с & Как и в примере, показанном на фиг. 1, если все тонкостенные балочные полки пересекаются вдоль одной и той же оси O (214), результирующая сила сдвига проходит через эту ось, и одна и та же ось явно является осью центра сдвига. * Здесь мы заключаем из предыдущего рассуждения, что внешняя сила должна быть распределена вдоль оси центра сдвига, чтобы получить простой изгиб балки (изгиб без скручивания) в целом и обратно к изгибу несимметричного beam.
To вычислить прогиб, вызванный этими силами, можно тем же методом, что и для чистых изгибов (см.§ 50).Каждая сила разлагается на 2 составляющие, параллельные главной центральной оси поперечного сечения балки, и изгиб балки в каждой главной плоскости рассматривается с использованием обычного уравнения балки, а отклонение, найденное в 2 главных плоскостях, может быть получено геометрическим сложением. ух…
Другим способом является выбор осей y и d, параллельных стенкам и полкам балки, как показано на рисунке. 212, разложить действующие боковые силы на 2 составляющие, соответственно параллельные осям y и r, и применить формулу (131) к силам плоскости xy. Аналогичная формула может быть выведена и для сил в плоскости xy. Окончательное отклонение получается геометрическим сложением*
Смотрите также:
Предмет сопротивление материалов: сопромат
| Изгиб, сопровождаемый растяжением или сжатием | Чистый изгиб в плоскости, которая не является плоскостью симметрии |
| Внецентренная нагрузка короткой стойки | Изгиб балок, имеющих две плоскости симметрии |

