Оглавление:


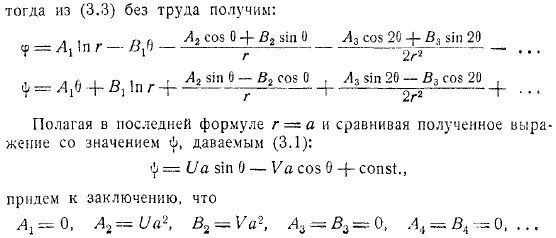







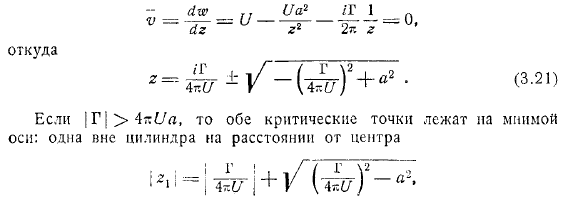

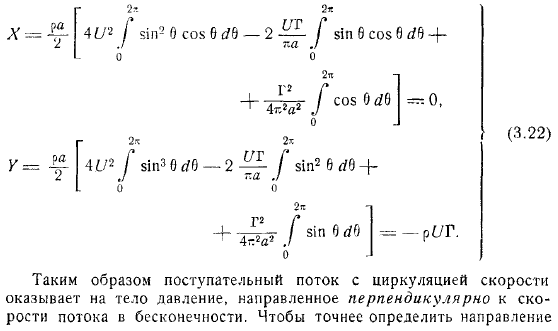


Движение кругового цилиндра
Одним из простейших случаев плоских задач является задача о движении цилиндра в жидкости без границ. Возьмите плоскость, перпендикулярную генератору цилиндра, и поместите начало координат в центр окружности, но плоскость пересекает поверхность цилиндра. Радиус окружности должен быть равен гидромеханике. Очевидно, что это круговое движение вытекает из плоской задачи, определяющей невращательное движение внешней окружности. Проекция скорости этого движения на оси координат цилиндра с поступательным движением, которая характеризуется.
- Тогда мнимая часть комплексного потенциала должна удовлетворять условию в окружности, как установлено в предыдущем разделе. Проекции скоростей являются однозначными функциями и стремятся к нулю, когда точка бесконечна. Это происходит потому, что условия жидкости неподвижна из-за предположений. Таким образом, комплексная скорость является единственной аналитической функцией вне круга. Исчезнет в точке Бесконечности.
К тому времени эта функция расширяется, и когда ряд рябины вида интегрирует это равенство и отбрасывает неважную аддитивную постоянную, получается следующая формула. To определим коэффициент, отделим мнимую часть, введем значения окружности формулами полярных координат, установим граничные условия Дирихле и Неймана. Тогда можно легко получить из сравните полученную жизнь со значением. Таким образом, мы приходим к выводу, что.
Кроме того, предполагая, что общее решение задачи задачи получается в виде то в простейшем случае это будет. Но точно такой же комплексный потенциал, есть поток от постоянного тока-лето, помещенного в центр цилиндра.и его оси направлены к положительной оси. Линии тока в обоих случаях будут одинаковыми, и вы получите диаграмму потока, показанную на диаграмме. Аналогичным образом комплексный потенциал соответствует дублету начала координат, а его направление совпадает с направлением скорости цилиндра.
Комплексный потенциал определяет интенсивность вихря, который находится в начале координат. Таким образом, рассматриваемый поток за счет движения цилиндра получается в результате наложения дублета, расположенного в одной и той же точке, которая направлена вдоль скорости цилиндра, на вихревую точку любой силы, расположенную в центре цилиндра и имеющую значение скорость цилиндра.
Из полученного решения нетрудно получить решение другой задачи, а именно задачи об обтекании неподвижного цилиндра с бесконечной скоростью, заданной по величине и направлению. Эта скорость выражается как поступательный поток, проекции скорости которого на координатную ось являются комплексными скоростями, поэтому комплексный потенциал если круг движется постепенно со скоростью, а жидкость бесконечно неподвижна, то поток, полученный вне круга, определяется комплексным потенциалом согласно предыдущему примеру.
Добавление этого комплексного потенциала к комплексному потенциалу дает. Очевидно, что в результирующем потоке имеется проекция на бесконечно удаленные. Также ясно, что условие обтекания окружности выполняется, поскольку обтекание этой окружности дают нормальную составляющую скорости, которая может быть вычтена при взаимном. Используя обозначение, можно преобразовать выражение. Он также может быть записан в формате когда бесконечно большой расход направлен вдоль оси и циркуляция скорости устранена, она становится.
Это последнее уравнение определяет поток без циркуляции по окружности в этом последнем случае, если вы снова используете полярные координаты, линия в этом последнем случае ясно, что это это не тот случай. Оставшаяся линия потока — это. Следующий рисунок. Получим величину при, и таким образом для скорости в направлении по касательной к окружности. В терминах контура. Максимальное значение составляет, достигая в конце диаметра перпендикулярного направлению бесконечно большой скорости. Значение скорости равно в терминах симметричной окружности относительно осей. Такая же вещь.
В большинстве случаев под цилиндром подразумевается прямой круговой цилиндр, у которого направляющая — окружность и основания перпендикулярны образующей. У такого цилиндра имеется ось симметрии. Людмила Фирмаль
А для стабильного и невращающегося движения несжимаемой жидкости без массовых сил (всегда учитываемых, если не сделано специального оговорки) давление определяется из интеграла Бернулли. Ясно, что давление будет одинаковым с точки зрения симметричной окружности по отношению как к оси, так и к оси. И понятно, что давление, оказываемое на элементы круга с, уравновешивается друг с другом. Поэтому поток вызываемый движущимся круговым цилиндром без поступательной циркуляции идеальной жидкости не оказывает давления на цилиндр в предположении, что поток является.
- Чисто циркулирующий устойчивый поток, каждая частица движется равномерно со скоростью. Частица в начальный момент с радиусом представляет собой кривую, уравнение которой очевидно, что чисто циркуляционный поток не оказывает результирующего давления при обтекании цилиндра. Когда чистый циркуляционный поток прикладывается к поступательному потоку вокруг неподвижного цилиндра, результирующий поток теряет симметрию по отношению к прямой линии через центр цилиндра, параллельной скорости потока при.
В этом случае комплексный потенциал потока находится из где скорость на бесконечности, направленная вдоль оси скорость циркуляции при повороте цилиндра в положительном направлении. В зависимости от соотношения абсолютных величин, установившийся поток принимает различное. То исследуя схемы течения, вы определяете точку потока, скорость которой равна нулю. Такая точка называется критической. Эти точки определяются квадратными уравнениями обе критические точки находятся на мнимой оси: вне цилиндра вдали от центра, вне расстояния, внутри.
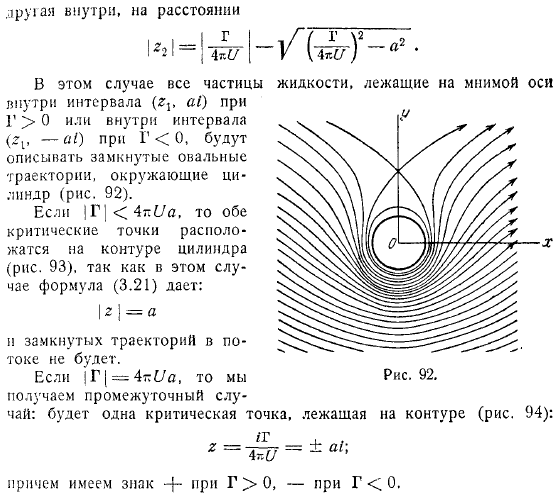
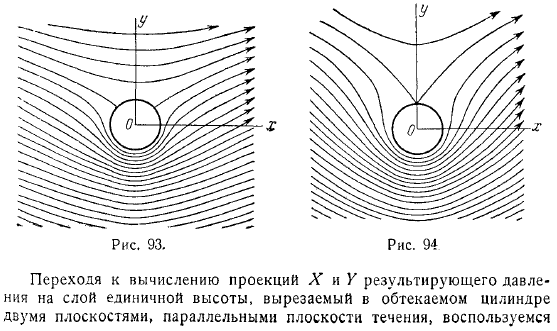
В этом случае все частицы жидкости, лежащие на воображаемой оси в интервале, представляют собой замкнутые эллиптические орбиты, окружающие цилиндр -. в случае обе критические точки лежат на контуре цилиндра. В этом случае, поскольку выражение дает. В потоке нет замкнутой траектории. Если, то мы получаем промежуточный случай. На схеме имеется важная точка. Кроме того, если символ, если поток плоскости, параллельной плоскости по упорядочению цилиндра были сокращены на единицу высоты слоя давление, создаваемое проекции в расчете на перевал, интеграл, используя следующий получает.
Где находится на нормальную внешнюю сторону является дуга элемента контура, потому что. На контуре цилиндра скорость является суммой скорости и скорости однако, поскольку поток является чисто круговым, поступательный поток с циркуляцией скорости имеет бесконечно направленное давление, перпендикулярное скорости потока на поверхности цилиндра. To более точно определите направление результирующего вектора давления, оно будет.
В обоих случаях вектор скорости потока должен быть повернут бесконечно под прямым углом, чтобы получить направление вектора. парадоксальный результат синтетического давления синтетического потока находит описание чистого поступательного и чисто кругового и асимметричного потока, возникающего в результате присоединения этих потоков к его составному потоку.
Например, если взять точки пересечения контура цилиндра с осью, где вектор скорости компонентного потока коллинеарен, то можно увидеть, что результирующая скорость меньше результирующей скорости в точке наверху, где эти скорости противоположны направлению. Таким образом, как следует из интеграла Бернулли, давление в точке выше цилиндра больше давления в точке ниже, что объясняет возникновение результирующего нисходящего давления. Формула является специфическим выражением формулы Кутта-Жуковского, которая может быть применена к любой форме непрерывно обтекаемых контуров.
Другие виды цилиндра — (по наклону образующей) косой или наклонный (если образующая касается основания не под прямым углом); (по форме основания) эллиптический, гиперболический, параболический. Людмила Фирмаль

