Оглавление:




Симметричные балки из двух различных материалов
Могут использоваться балки из 2 и более различных материалов. Рисунок 195, а представляет собой простой случай деревянных балок, усиленных стальными полосами, прибитыми к балке снизу. При изгибе, предполагая, что нет проскальзывания между Сталью и деревом, здесь также может быть использована теория сплошных балок.
- Согласно этой теории, удлинение и укорочение продольных волокон пропорционально расстоянию от нейтральной оси. В связи с тем, что модуль упругости древесины значительно меньше модуля упругости стали, как показано на рисунке, деревянная часть балки при изгибе соответствует очень узкой стенке из стали. 195, b. So чтобы момент внутренней силы не изменялся относительно некоторой кривизны, то есть до определенного удлинения и укорочения, толщина этой стенки b \имеет следующий вид: 。 (ля) Рисунок 195. Таким образом, задача сводится к изгибу стальной балки Т-образного сечения, которая называется преобразованным сечением.
Эта проблема может быть решена на основе предыдущих теорий. Людмила Фирмаль
Например, рассмотрим балку длиной 3 м, свободно лежащую с усилием 400 кг в центре. Горизонтальное измерение Сечение деревянной части балки: 6 * = 10 см, Н-15 см, выпуклость усилена стальной полосой шириной 2,5 см и толщиной 1,25 см. используя £d / £c = 1/20, уравнение (a) имеет деформированный поток стенки 15×0. 5 см и полка 2,5 х Х1. 25 см расстояние крайних волокон от нейтральной оси рисунка 195, где b равно hi-6,36 см nA * = 9,9 см.
Поскольку момент инерции преобразованного участка относительно нейтральной оси равен/,= 290 см4, то экстремальное напряжение волокна преобразованного участка (из Формулы (61)) 30000 ^ 35 ^ 655 кг \ см \ Максимальный. н0,000, 9 ^ ^ = 1024 кг {см \ ^ млн. Чтобы получить максимальное напряжение сжатия в фактической древесине балки, напряжение преобразованного поперечного сечения (сталь), полученное выше, применяется к C1N£d / £c = 1.It необходимо умножить на /20.
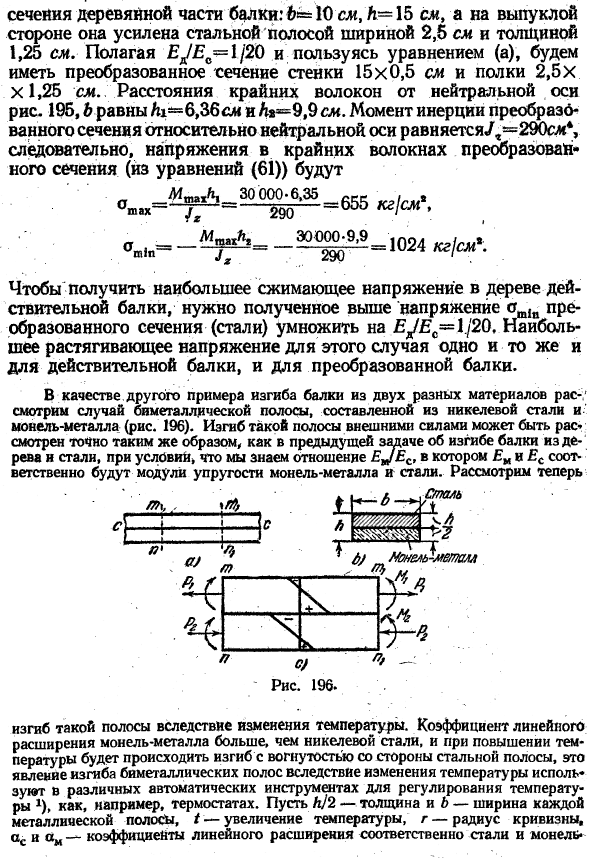
Максимальное растягивающее напряжение в этом случае такое же, как и в реальной балке. Преобразованный луч. В качестве другого примера изгиба балки из 2 различных материалов Рассмотрим случай биметаллической полосы, состоящей из никелевой стали и металла Монеля(рис.196).Изгиб таких полос под действием внешних сил можно рассматривать точно так же, как и в предыдущей задаче изгиба балки РО звук железа.
- Однако, если известно соотношение E ^ EC, Ey и Ec являются модулем упругости металлов Monel и стали соответственно. Подумайте об этом сейчас < Звезда / б \ М、 быстрое преобразование Фурье. \、 1.1 второй л. y 3 а / nonel^металла ПБ В / Л. П’. один.) П. С. * К л. 7> в. х. с. / Рисунок 196. Изгиб таких полос обусловлен изменением температуры.
Коэффициент линейного расширения металла Монель больше, чем у никелевой стали, и при повышении температуры происходит изгиб, изгиб в вогнутой форме со стороны стальной полосы. 。 / g / 2 толщина каждой металлической полосы, B ширина, f повышение температуры, r радиус кривизны, ac и am коэффициент линейного расширения стали и Монеля соответственно и жесткость изгиба металла,£СУС-сталь, £ мум-Монель Жесткость изгиба металла.
При повышении температуры металлическая полоса Monel с высоким коэффициентом теплового расширения подвергается изгибу и сжатию, а стальная полоса изгибается и растягивается. Принимая во внимание элементы полос, выделенные смежными 2 поперечными сечениями mn и fn | l} (рис.196, В), можно направить внутренние силы вдоль поперечного сечения на растягивающую силу P и пару Mg. —
Металл может быть уменьшен до коэффициента сжатия P1 и MX пары. Людмила Фирмаль
Внутренняя сила поперечного сечения балки должна быть balanced. So … П= П — П И так далее. 。 £ = м,+ м,. (Си) Вставить.. ЕСЕО.. МЛ = — ±М= — Г — Г、 Я г * * г К формуле (b)、 2 г 71 г . (с> Другое уравнение для определения буровой установки может быть выведено из условия, что относительное удлинение металла и стали Монеля вдоль контактной плоскости c_c равно same. So … •. 2Р 2Р. А. «С+ Ш ^ + ТГ」 Или Получаем 4 из формул © и (b) ^(£^ +£* 7 *)(экс-Б (£М)-(АМ-АС)£г (ми)) Yb.
Вставить в это уравнение г р БК^,, Р „С-м ^ с-1/15£м」 Получим следующее приблизительное выражение: 1. 3 (утро и утро)/ (Да 7 г-2 л . Теперь из уравнения © 3.. Да°c) (^ L “ — ’ M » mu-22 П-Ла — °С)^ (^С ^ С Не ^ м ^ м)-49(°м-°с> ^(^ С» Б ^ М) (6) «3 (м-ОС) * 17 г ЛЛ 3 (дм-ОС) / г.、 ^ 1 2 L s * 3 2 L » gm Из уравнений&) и (b), P, M и L * a можно определить максимальное напряжение В случае стали она получается путем сложения растягивающего напряжения, вызванного силой Р, и растягивающего напряжения от кривизны- (£^з + ^ з +%ф
Например, если предположить, что модуль упругости E обоих металлов одинаков、 °Max xL » •или используя формулу (/) 1)、 。 ^ у * х = 4 — £^ с «» — переменного тока)- = = 1.8-10 eягg / CM®, / = 200 ° C и am — AC = 4 * 10〜® ^Шах^ 720 кг / СМГ. На рисунке показано распределение напряжений, возникающих при нагреве. 196, стр.
Задачи 1. b = 15 см, L = 20 см, если толщина стальной полосы составляет 1,25 см, найти допустимый изгибающий момент деревянных балок, армированных стальной полосой (рис.195) Ea = 10 * кг / СМГ, принять Ec =2′, cm2 = 1 кг/ СМГ-если древесина, [os / kg / kg] = 8070 кг / кг], если сталь 109 см.
2.Деревянная балка в предыдущем задании предполагает, что верхняя часть армирована полосой из стали шириной 5 см и толщиной 2,5 см, нижняя часть армирована полосой из стали шириной 15 см и толщиной 1,25 см. То же, что и в предыдущем задании. Ответ. L4 = 308 000 кг см. Д 3.Длина биметаллической полосы составляет f = 2,5 см. c= 1.15 am-ac при£m = 4-10 дюймов, если температура. Найдите центральное отклонение из-за подъема на 200°C. *
Смотрите также:
Предмет сопротивление материалов: сопромат
| Железобетонные балки | Неразрезные балки |
| Касательные напряжения в железобетонных балках | Балки переменного поперечного сечения |

