Балки переменного поперечного сечения

Балки переменного поперечного сечения

Балка переменного сечения В предыдущем пункте рассматривался призматический луч. Более детальное исследование показывает, что Формулы (56) и (57), полученные для стержней призмы, могут быть применены с достаточной точностью для стержня переменного сечения, если изменение не слишком sharp. In в случае резкого изменения поперечного сечения, то, в котором сосредоточено напряжение, разлагается в N-й части.

• В качестве первого примера балки переменного сечения рассмотрим кантилевер равного сопротивления, то есть изгибающий момент и изгиб балки, при котором длина сопротивления изменяется вдоль ее длины в одинаковом соотношении. Тогда, как видно из Формулы (60), величина (a) ω ＃ х остается постоянной по длине пучка и может быть равна (o].

Такие условия благоприятны с точки зрения количества используемого материала, так как каждое сечение минимально. * Зона для того чтобы соотвествовать прочности. Рисунок 187. Для консоли с грузом на конце (рис. 187) изгибающий момент поперечного сечения на расстоянии х от груза численно равен Px.

To получить пучок равного сопротивления, момент сопротивления также должен быть пропорционален x. это условие может быть выполнено в различных ways. As в качестве примера рассмотрим случай, когда ширина равна b, а высота равна h-это постоянное прямоугольное сечение(рис.187).

Из определения понятия равного резистивного пучка、 М. 6Pxt».. БФ = ^ = const и ’■ Г. х’х. Где k-высота балки на герметичной кромке. Тогда К2 = В этом случае, согласно закону параболы, можно видеть, что высота луча changes. At конец нагрузки, поперечное сечение нул.

В практическое применение, эти напряжения должны быть приняты во внимание, чтобы иметь достаточную площадь поперечного сечения для поглощения боковых сил из-за изменения формы на конце нагрузки. Последнее отклонение луча можно определить из уравнения (93). 1Т 1. Т C \ 2 пикселя * \ ДХ оказываемых 2PL 2 пп / ИО!4. ФН-в ^ = М? yxdx = ^ ЗТ. ’< 121> 0 * ОО 。 КТГ Где J0 = — jg-представляет собой момент инерции сечения Конец патча.

Этот результат получается при выводе формы балки, которая равна сопротивлению, поскольку напряжение сдвига игнорирует axis. Людмила Фирмаль

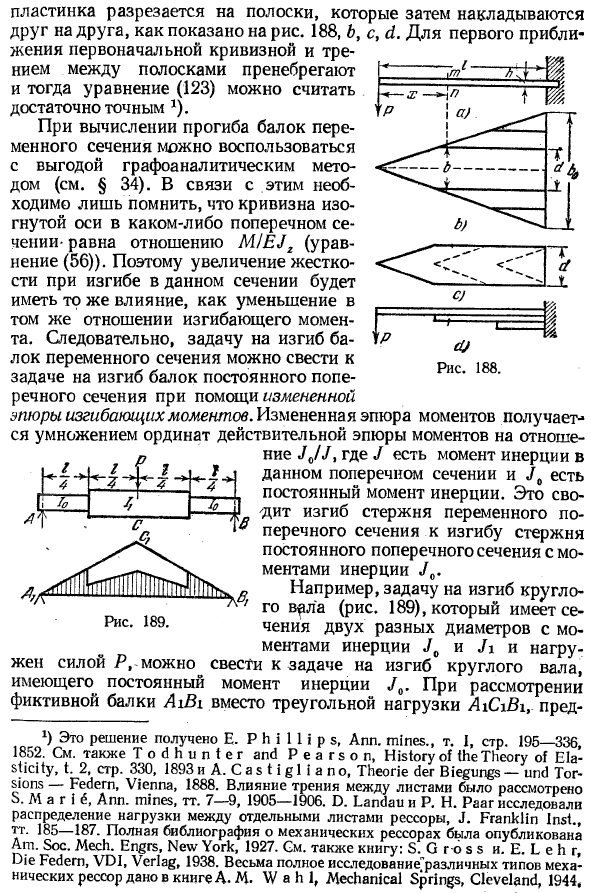
Сравнивая с уравнением (95), можно видеть, что это отклонение в 2 раза превышает отклонение стержня призмы при той же нагрузке, что и изгибная жесткость EJ0.То есть стержень имеет ту же прочность, что и стержень призмы, но не ту же жесткость. В качестве примера 2-го рассмотрим кантилевер с прямоугольным поперечным сечением постоянной высоты h и переменной ширины b (рис.188, а и 188.6).

Максимальное напряжение (tfx) max и кривизна (см. формулу (56)) остаются постоянными по длине балки, поскольку момент сопротивления и момент инерции треугольной балки Jr увеличиваются с увеличением x в той же точке, что и изгибающий момент. Радиус кривизны можно определить по формуле(см. формулу (55)). 。 \ Е.、 2г. *（） Прогиб на концах дуги окружности равен случаю малого прогиба т-ш-м <| 22> Или используя формулу (a) / «(«А«,£•(123>

Это выражение указывает, что данный тип консоли равен Сопротивление, отклонение края меняет в пропорции к квадрациклу Она обратно пропорциональна длине и высоте. Этот результат может быть использован для аппроксимации напряжения и прогиба листа geometry. As показанные на рисунке пластины разрезают на полосы, после чего их накладывают друг на друга. 188, 6, s, C I. In в первом приближении начальная кривизна и трение между полосами игнорируются, и уравнение (123)считается очень точным. 

1) При расчете прогиба балки с переменным поперечным сечением можно воспользоваться методом графического анализа (см.§ 34).в связи с этим следует помнить, что кривизна криволинейной оси любого поперечного сечения равна соотношению ШIig (Формула (56)).Поэтому увеличение жесткости на изгиб в конкретном сечении имеет тот же эффект, что и уменьшение того же изгибающего момента ratio.

• Когда в результате задача изгиба балки с переменным поперечным сечением может быть сведена к задаче изгиба балки с постоянным поперечным сечением, используя следующее: ..- \м. .. — Лл м. Х-Щ / 7Т ИС 1 а） Иллюстрация изгибающего момента. Модифицированная диаграмма моментов получается путем умножения отношения Jc / Jt на ординату фактической диаграммы моментов.

Где 3-момент инерции для данного участка, а/ 0-постоянный момент инерции. Это уменьшает изгиб стержня переменного сечения до изгиба стержня постоянного сечения с моментом инерции J0. uф> к * — дл *.Извините. 4. ; К-4] Рисунок 189. Например, существует 2 различных по диаметру сечения момента инерции J0 и Jl, а задача изгиба круглого вала vrl (рис.189), где сила P нагружена, может быть отнесена к задаче изгиба круглого вала с постоянным моментом инерции (J0).При рассмотрении фиктивной балки авіі на месте треугольной нагрузки аіііі * )

Это решение, E. It был получен Филлипс, Энн. Мой, Том 1, 195-336, 1852.Тодхантер и Пирсон, история теории упругости, т. к. 2, p. s. 330, 1893 и A. Castigliano, Theorie der Biegungs-und Torsions-Federn, Vienna, 1888.Мы учитывали эффект трения между листами С. Maggue 1, Энн. Мой, Тома 7-9, 1905-1906. Д. Ландау и Р. Х. Паар исследовали распределение нагрузки между листьями отдельных листьев. J. Franklin Inst. ВОЛС. 185-187.Полная библиография механических пружин была опубликована Ам. Соц. Меха Engrs, Нью-Йорк, 1927.

Смотрите также книгу: С. с Гроссом. Е. Л е ч, умереть Federn, ВДИ, издательство, 1938.«Очень полное исследование различных типов механических пружин было проведено в 1944 году a. A. механических пружин Кливленда. М. Вал. При установке значения изгибающего момента от действительной нагрузки используйте нагрузку, представленную заштрихованной областью.

Эта площадь получается путем уменьшения ординаты участка Центрального сечения вала относительно / / / b. определения прогиба^и угла наклона следующие: в случае призменных стержней; величина прогиба и угол наклона в любом поперечном сечении балки равны величине, полученной путем деления поперечной силы от изгибающего момента и мнимой нагрузки на EJ.

Происходит резкое изменение диаметра вала на 189, расстояния от опоры/ / 4, и в этих точках возникают локальные напряжения. Если разница в диаметре 2 секций невелика по сравнению с длиной этих секций, то это не оказывает существенного влияния на изгиб вала. Людмила Фирмаль

Метод, примененный к валу с переменным поперечным сечением, также может быть применен к композитным двутавровым балкам. •. •. 。Или на запущенную ферму.： Переменная поперечная стенка * ток. На рисунке показан пример фермы с сплошной стеной, которая поддерживается на конце и нагружается равномерно. 190.

Изгибающий момент уменьшается от середины к краям фермы, а вес балки можно уменьшить за счет уменьшения количества листов в поясе.4 sah как показано на рисунке л. На фото. Отклонение такой балки можно рассчитать исходя из момента инерции среднего Креста section. In в случае мнимой нагрузки вместо 1 параболы, обозначенной пунктирной линией, уменьшение сечения фигуры 1 компенсируется увеличением ординаты фигуры момента до Lered /» / 190 заштрихованной области.

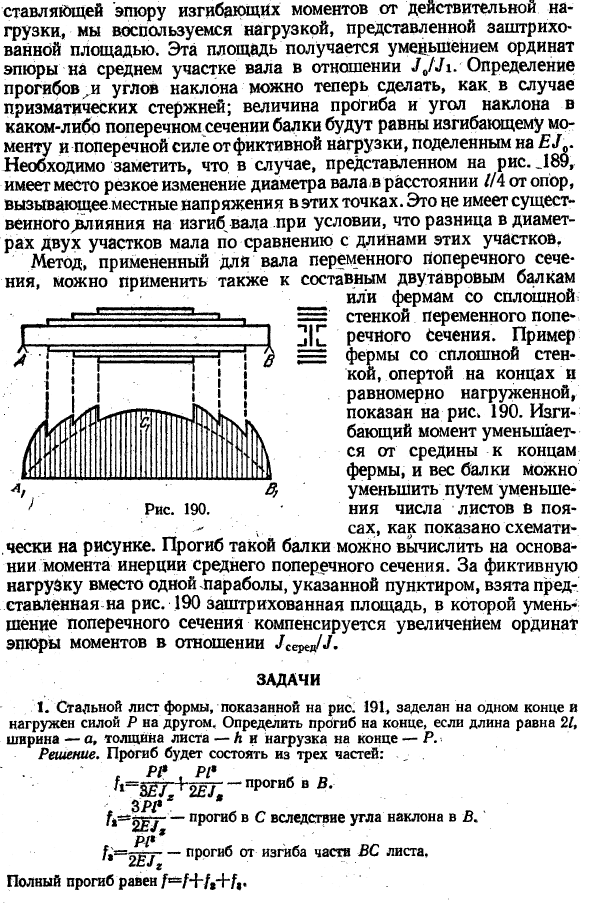
Задачи Я… Форма стального листа 191, показанного на рисунке, запечатана с одного конца, а сила P нагружена с другого конца. Определите прогиб ребер, если длина равна 2/, ширина равна а, а толщина листа равна. Является ли конечная нагрузка R. Решение. Прогиб будет состоять из 3-х частей. • ’, Р19. R1Sh * а ■ / / / 1 / Кровяное давление * Прогиб с углом наклона Б Р1 * 9 Отклонения от изгиба части солнечного листа.

Суммарный прогиб/ = / + / * + / а.2. / — ==26 см, 7,6 см, I = » 400 кг и = 4800 кг / см максимум.; 8. liszd определяют ширину d P = 2.5 t, d » * 1; 25 см,/ = 60 см, {o]» (Инжир. 188) и его отклонение, кг! см *и номер листа l = 10 Решение. Если учесть, что трамплин вырезан из треугольной пластины(рис. 188.6), то максимальное напряжение найдено _6I. / Откуда? J 6Y./ 6 * 2500 * 60 _10 Л [О] в * G1o-48b0. 1. 25 * см ’ Отклонение определяется по формуле (123, 4800 * 60 * в Q1 6.91 см 4.

Сравните центральный прогиб с углом поворота обоих концов вала, показанным на рисунке 2. 189, имеет такую же площадь поперечного сечения с таким же осевым размером и такой же длиной, и свой момент инерции J0.Я согласен. Решение. Из-за высокой жесткости в среднем изгибе угол поворота конца вала, показанного на фиг. 189, меньше угла поворота конца цилиндрического вала, если заштрихованная область меньше всей площади треугольника AXXX±.Общая площадь представляет собой нагрузку на цилиндрическую ось.

Для указанного значения это соотношение составляет 5/8: 1. Центральный прогиб обоих валов имеет такое же отношение, как изгибающий момент от области штриховки и области треугольника AXXXBX. Это соотношение составляет 9/16:1.* ч a. As как показано на рисунке, нагрузка приложена к балкам, которые поддерживаются на обоих концах. 192, если ширина b прямоугольного сечения остается постоянной по длине балки, как изменить высоту L балки, чтобы получить равную форму сопротивления?

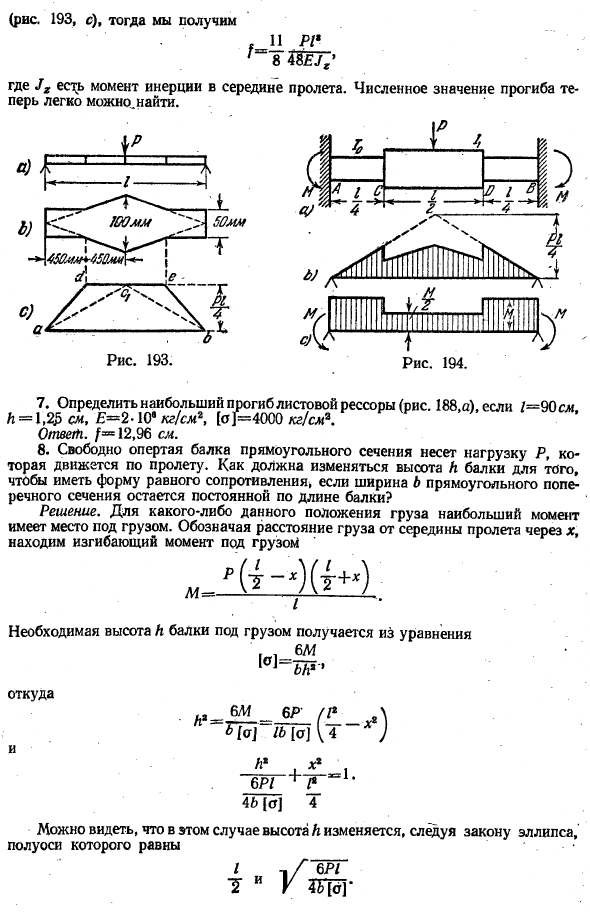
Ответ 6.Рисунок 1.25, имеющий толщину 1.25 см, определяет прогиб стального листа. 193, и 193.6, когда нагрузка 10 кг в центре. Решение. Уменьшите эту задачу и определите прогиб пластины с постоянной шириной, равной 10 см. Диаграмма моментов в этом случае преобразуется в трапецию.11. П1. * 8 SHGg」 — Момент инерции центра пролета. Фигуры отклонения Перья простые, ночные. Так… 7. 1 = 90 см, h = 1,2£см,£= 2-10 кг / см2, (o] = 4000 кг! Для см2 определите максимальное отклонение листовой рессоры(рис. 188, О). Ответ. / = * = 12,96 секунды, И. 8.

Свободно поддерживаемая балка прямоугольного сечения несет груз Р, перемещающийся вдоль пролета. Если ширина b прямоугольного сечения остается постоянной по длине балки, то как должна изменяться высота h балки для получения одинаковой формы сопротивления?

Решение. Для любого положения нагрузки, максимальный момент происходит под нагрузкой. Расстояние нагрузки от центра пролета до x указывает на изгибающий момент под нагрузкой. п(й-Х){У + Х） М. Я… Требуемая высота L балки под нагрузкой определяется по формуле 6 М * А 」 Откуда? Λ =—6р / / £[σ] 1Б(п） (Т-） 1. 46 [a] 4 В этом случае видно, что по высоте 6 изменяется, согласно закону эллипса, где полуось равна. 9.

Когда оба конца герметизированы и нагрузка приложена к центру пролета, определите опорный момент на конце балки AB(рис.194).Я согласен. Решение. Решение получается путем сложения 2 простых случаев, которые показаны на рисунке 2. 194 БИС.

Если угол поворота торцов равен нулю, то есть реакции от мнимой нагрузки (см. стр. 139), представленной штриховкой области Б) и в), то понятно, что условие герметичности торцов равно met. So, уравнение, определяющее числовое значение M, выглядит следующим образом: 4 2 8 4 2 4 * / Откуда? 10.Решает предыдущую задачу в предположении, что приложена нагрузка P, равная точкам C и прилож>. Ответ. М.

Смотрите также:

Предмет сопротивление материалов: сопромат

Симметричные балки из двух различных материалов	Балки на трех опорах
Железобетонные балки	Неразрезные балки