Оглавление:








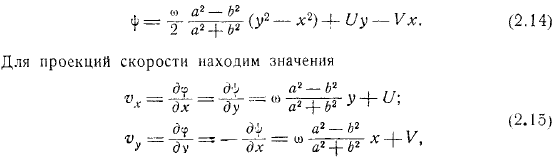

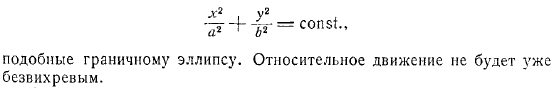

Граничные условия. Задачи Дирихле и Неймана
Поиск комплексного потенциала, определяющего планарное невращательное движение несжимаемой жидкости гидромеханики, можно свести к поиску функции потока, поскольку потенциал связан с известными условиями Коши. Римана, из известной функции можно определить в виде квадратуры. Функция потока, которая считается непрерывной во всех точках течения несжимаемой жидкости, удовлетворяет уравнению Лапласа в этих точках, а на определенных границах течения-некоторым известным условиям. Формат зависит от реализации квартиры.
Показаны простейшие случаи, без цели исчерпывающей классификации различных типов граничных условий. Рассматривая плоское течение бесконечно статичной бесконечной жидкости о движении тела в идеальной жидкости, возникающее при движении цилиндра, граничные условия для функции потока однозначно следующие — поскольку скорость в этих точках должна быть равна нулю. В каждой точке контура движущегося тела, нормальная проекция скорости должны совпадать.
- Угол между элементом линии потока и осью, а соотношение между позволяет выразить рассматриваемое условие. И если в жидкости еще есть неподвижный объект, то по их контуру понятно, что обычная составляющая скорости соседних частиц жидкости должна быть равна нулю, другими словами, сам неподвижный контур должен находиться в контакте с текущей линией. В этом случае необходимо добавить граничное условие к предыдущему условию. Для точки фиксированного контура.
Если тело движется поступательно со скоростью, направленной вдоль оси, то условие равно. Принять форму, или все точки контура, после того как цилиндрический объект совершает какое-либо движение. При наличии поступательного потока с бесконечно большой скоростью расстояние до удаленной точки равно, ориентированной вдоль оси и обтекающей неподвижный объект. Граничное условие, очевидно, выглядит так: для бесконечности показанные нами граничные условия в основном используются при исследовании стационарного движения, но остаются справедливыми для нестационарного потенциала.
В этом случае предыдущее выражение вводит только время в качестве параметра. Параметры зависят от. Известное значение функции на контуре области называется задачей Дирихле, хотя это задача определения функции, удовлетворяющей уравнению Лапласа в области. Таким образом, мы видим, что определение плоского невращательного движения несжимаемой жидкости, вызванного движением контура, ограничивающего область течения, приводит к решению конкретной задачи Дирихле.
При решении гидродинамических задач можно также сначала найти все потенциалы скорости. Он также должен удовлетворять уравнению Лапласа в области течения. Но является ли граничное условие схемы необходимым для функции? Другой само определение потенциала скорости является вертикальной проекцией в скорости частицы жидкости, прилегающие к контуру, и, следовательно, граничное условие для функции принимает форму an является нормальной проекции скорости точки контура. В частности, в терминах фиксированных границ, мы получим условие.
Моделью идеальной жидкости пользуются при теоретическом рассмотрении задач, в которых вязкость не является определяющим фактором и ею можно пренебречь. Людмила Фирмаль
В области, задача определения функции, которая удовлетворяет уравнению Лапласа по известному значению нормальной производной функции на контур области называется задачей Неймана. Поэтому гидродинамические задачи приводят к решению некоторых задач Неймана. Вы можете использовать функцию для определения функции и наоборот. Поэтому ясно, что задача Неймана может быть сведена к задаче Дирихле, или наоборот. Факт, запомните состояние Коши-Римана и проследите за цифрой некоторое время.
Направление нормали в направлении оси, и направление касательной в направлении оси, получаем следующие соотношения сразу, вы можете перейти к задаче Неймана из задачи Дирихле, если есть проблема Неймана, то есть, если вы знаете значение на схеме, это будет следующим образом. Переходим к границе области течения, и поэтому Дирихле. В случае задачи многосвязной области с границей на контуре предыдущее выражение отображает значение аддитивной постоянной для каждой схемы. По значению одной из этих аддитивных констант движение определяется значением производной функции, поэтому его можно выбрать.
Любые константы в будут отображаться. Дана циркуляция скоростей по контуру, которые неприводимы друг к другу. Это полностью совпадает с замечанием о том, что вращательные движения, сделанные в конце раздела главы движение кругового цилиндра , полностью определяются задачей. И цикл только в том случае, если настройка циклическая. В качестве простого примера рассмотрим задачу о невращательном движении несжимаемой жидкости, заключенной в эллиптический цилиндр. Пусть эллиптическое уравнение.
- Его движение характеризуется проекцией на координатную ось скорости и угла поворота скорости его центра. Тогда функция потока должна удовлетворять уравнению в эллипсе и граничному условию самого эллипса. Полином порядка. Я ищу функцию в виде. Уравнение представляет собой отношение. Уравнение из условия является результатом. Это означает связь между для проекции скорости найдите значение, вы можете получить оттуда легко.
Простейший случай чистого поступательного движения цилиндра, когда, выглядит так: то есть жидкость движется вместе со всем цилиндром. Для чистого вращения, когда, это выглядит так: линия потока абсолютного движения гиперболическая. Подчеркнем, что полученная нами формула определяет абсолютное движение жидкости, но относится к движущимся координатным осям.
Движение жидкости относительно этих движущихся координатных осей определяется вычитанием проекции переносной скорости из проекции абсолютной скорости. В результате проекция относительной скорости выглядит следующим образом и представляет собой эллипс, аналогичный граничному эллипсу. Относительное движение больше не является вихревым.
В частности, такая идеализация допустима во многих случаях течения, рассматриваемых гидроаэромеханикой, и даёт хорошее описание реальных течений жидкостей и газов на достаточном удалении от омываемых твёрдых поверхностей и поверхностей раздела с неподвижной средой. Людмила Фирмаль

