Неразрезные балки

Неразрезные балки

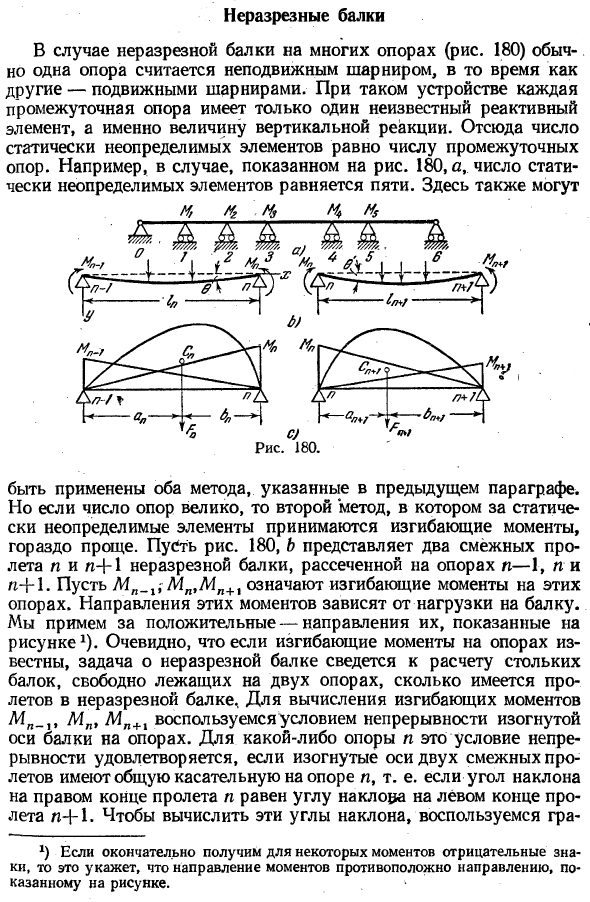
Неразрезная балка В случае непрерывных балок на многих опорах (рис. 180), 1 опора обычно считается неподвижным шарниром, а другая опора считается подвижной hinge. In в таком устройстве каждая промежуточная опора имеет только 1 неизвестный реакционный элемент-величину вертикальной реакции.

• Таким образом, число статически неопределенных элементов равно числу промежуточных опор. Например, в случае, показанном на рисунке 1, число элементов, которые не могут быть определены с помощью 180, a или статически, равно 5.Вы также можете здесь Применяются оба метода, указанные в предыдущем пункте.

Однако при большом количестве опор 2-й способ, принимая изгибающий момент за статически неопределенный элемент, гораздо проще. Давайте возьмем немного риса. 180, b представляет собой 2 смежных пролета n, n + 1 непрерывной балки, вырезанной в опоре n_1, n, n + 1. Mn_1; Mn, Mn + 1 означает изгибающий момент этих опор. Направление этих моментов зависит от нагрузки на балку.

Будем считать их положительными-их направление показано на рисунке 1. Людмила Фирмаль

.Очевидно, что если изгибающий момент опоры известен, то задача непрерывной балки состоит в том, чтобы рассчитать такое же количество балок, как и пролет непрерывной балки со свободным размещением в 2 supports. To рассчитайте изгибающий момент Mn_1, Mn, Mn + X, используя условие непрерывности криволинейной оси балки на опоре.

Для любой опоры n это условие непрерывности выполняется, если изогнутые оси 2 соседних пролетов имеют общую касательную к опоре n, то есть если наклон самой правой точки пролета n равен наклону самой левой точки пролета n. To рассчитайте эти углы наклона, используя график * )

• Если в какой-то момент появляется отрицательный знак, это указывает на то, что направление момента противоположно направлению, показанному на рисунке. To оптические методы анализа. От действительной нагрузки этого пролета мы имеем в виду площадь фигуры изгибающего момента пролета n (рис. 180, В), которая считается свободно несущей балкой. предположим, что an и bn представляют собой горизонтальное расстояние центроида Cn в области диаграммы моментов от опор n_1 и N.

Это условие нагрузки, самый правый угол будет (см.§ 36). В дополнение к изгибу, вызванному нагрузкой, которая находится в пролете, пролет N пар Mn_r и M. it также изгибается по п. из формул (103) и (104) угол, называемый n, поддерживаемый этими парами, равен следующим значениям:’… / Mnln»/» \ 6EJt у (ля） И полный угол поворота 1） интернет * ^ — ^ ^ — я Mn1n+, МН + мы + л «ln + xEJz + zezhz T 6 JEJZ•」

Аналогично, для левого конца пролета n + 1 получаем следующее: (си） Это уравнение 3 моментов 2). понятно, что число этих уравнений равно числу промежуточных опор, и поэтому изгибающий момент опор можно вычислить без труда. ух… Из условий непрерывности (с） Если вставить в это уравнение уравнения (а) и (Б) 、 / Первоначально предполагалось, что оба конца непрерывной балки поддерживаются.

Если один или оба конца герметизированы, то число статически неопределенных величин будет больше числа промежуточных опор, и можно вывести необходимое дополнительное уравнение условия, что герметизированные концы балок не вращаются (см. задачу 5 ниже). Зная момент на опоре, можно без труда рассчитать давление непрерывной балки. Людмила Фирмаль

Например, 2 смежных * ) Угол считается положительным, если вращение происходит по часовой стрелке. 2) это уравнение было получено Berio t, Comp t. это отличная игра. соц. Инг. См. также: граждане, пор, 278, 1855; Клапейрона, Compt, Ренд, Т. для. 45, 1857.Если рассматривать пролет n и n-f 1 (рис. 180, б) как 2 свободно опирающиеся балки, то можно легко рассчитать силу реакции an опоры p от нагрузки этих 2 spans. In кроме того, происходит реакция из точки отсчета ML_XU Mn, L4n + 1.

Возьмите направление этих моментов, как показано на рисунке. Существует дополнительное давление на 180, b и поддержку. * Н + / Б + ‘\ Если вы добавите это в react A, вы получите полный ответ, как указано выше! икс К ^ К + М -^) — н + — ^ + — н + ’-. — (119） * P * P +1 Если концентрации наносятся на носитель, то они передаются непосредственно на соответствующий носитель и должны быть добавлены в правую часть формулы (119).

Общее уравнение неразрывности © может также применяться, если опора не находится на одной высоте из-за неправильного размещения опоры или неравномерного закрепления опоры. (Рисунок 181). β „и p“ означает +1—- {———- Угол наклона относительно горизонта прямой линии-j ’7 * 7 * ’* L» -! * НИИ, соединяющей точки опоры для P-ГО и в период восстановления*% й»ф (l-N) —й пролет; угол поворота, U -.- £ — ^ Уравнения, определенные в (a) и (b)、

Измерьте от линии, соединяющей центр шарнира. Следовательно, угол 6 между касательной к l и горизонтальной линией будет проходить L • — (Да+% 1g + ï -’«） Точно так же и про пролет l-f-1 Ка 1 БН + 1 Mn1n + г / п + | ЛН + Т£ЮЖД 6EJ、 РЛ + 1 * * Если вы выровняете эти углы, вы увидите, что М «^1п+2Мп (LN + LN + t)+л4я + 1 / » + 1 = = — ^- ^D + — ttejt(β»+, — β«). (120） ln.* / 1 + 1 «_!Если Нп, Нн + 1 означает вертикальное расстояние опоры L-1, L и L + 1 относительно горизонтальной линии、 а »»» д ^ н ^ н + 1 Рп » 1″Ри + 1 = / 1 час 4 = 2,69 Т; Л,= 6.22 Т; Л= 3.75 Т; Л4 = −0.275 Т.

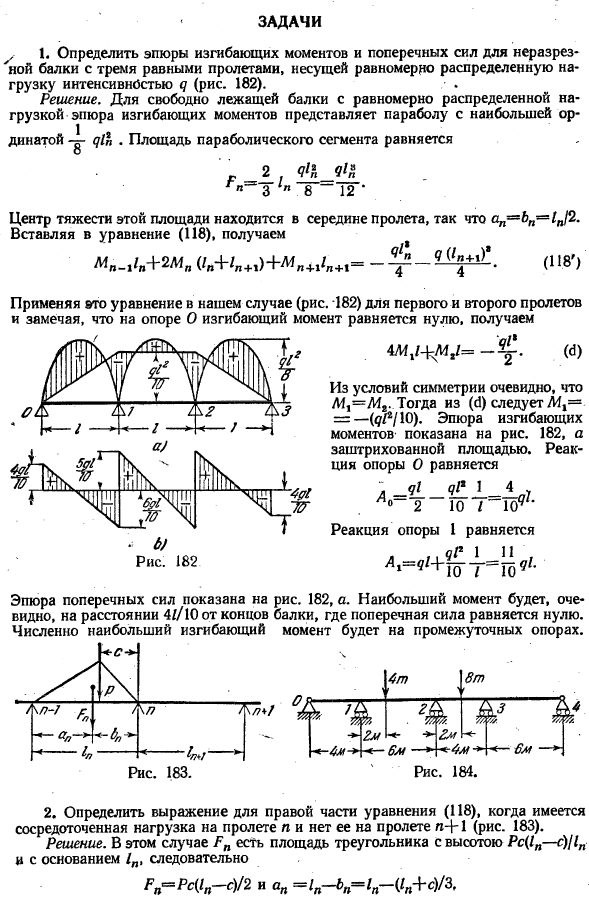
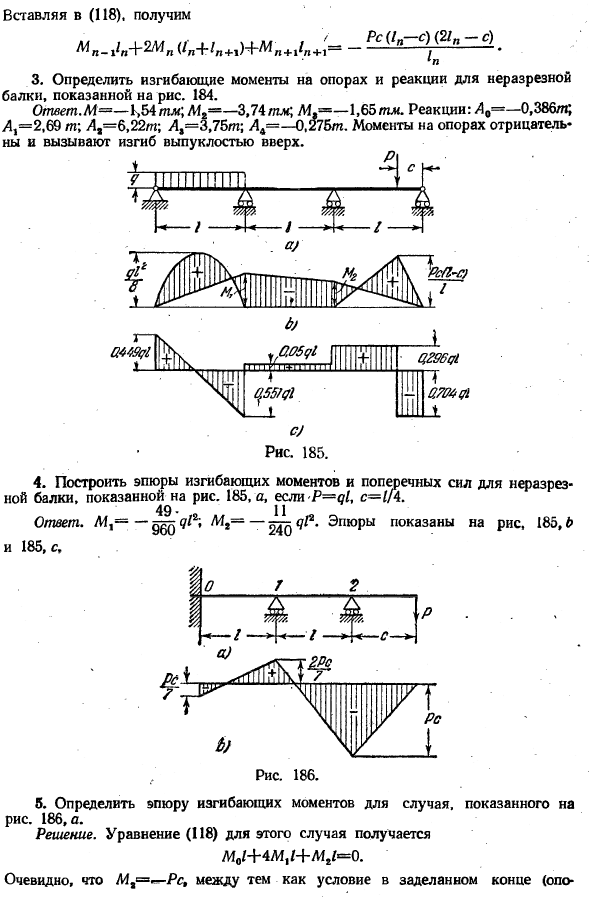
Момент поддержкой является отрицательным и согнуть вспучивается вверх. Я… 04SCH1. Ной. 49. * Ответ. А4= — \ ДП мг— 11. 240. 4.Создайте график изгибающего момента и силы сдвига непрерывной балки, показанной на рисунке. 185,а, ЕТП = Д1,с = 1/4. Рисунок 185 показан на рисунке. И 185 с а. определите величину изгибающего момента в случае, показанном на рисунке. 186 а.

Решение. Формула (118) в этом случае получается вообще-НЛУ + Лу ^ о Очевидно, Ya, состояние герметичного конца (опоры O) (из уравнений (103)и (104)） «Или П ’1 2 из приведенного выше уравнения получаем Л4Р= — Рс;. Л4#= — Яс. На рисунке показана схема изгибающего момента. 186. один. 6.Если только средний пролет взвешен с равномерно распределенной нагрузкой q, определите изгибающий момент непрерывной балочной опоры с 7 равными пролетами.

Ответ. Л4,=М4=-^М»Мг* =Мщ= ^М$. 7.В последний пролет равномерно загружается непрерывная балка длиной 4,8 м, каждая из которых имеет 4 равных пролета. Для < 7 = 500 кг / м постройте график изгибающего момента и силы сдвига. 8.Решаем задачу 5, предполагая, что равномерная нагрузка интенсивности q распределена по всей длине пучка, и что она равна—1/2.Постройте график боковых сил в этом состоянии нагрузки. Ответ, Л40=с&^ ^ **〜дРгМ ^ — no я^ *

Смотрите также:

Учебник по сопротивлению материалов: сопромату

Балки переменного поперечного сечения	Рамы
Симметричные балки из двух различных материалов	Балки на трех опорах