Рамы

Рамы

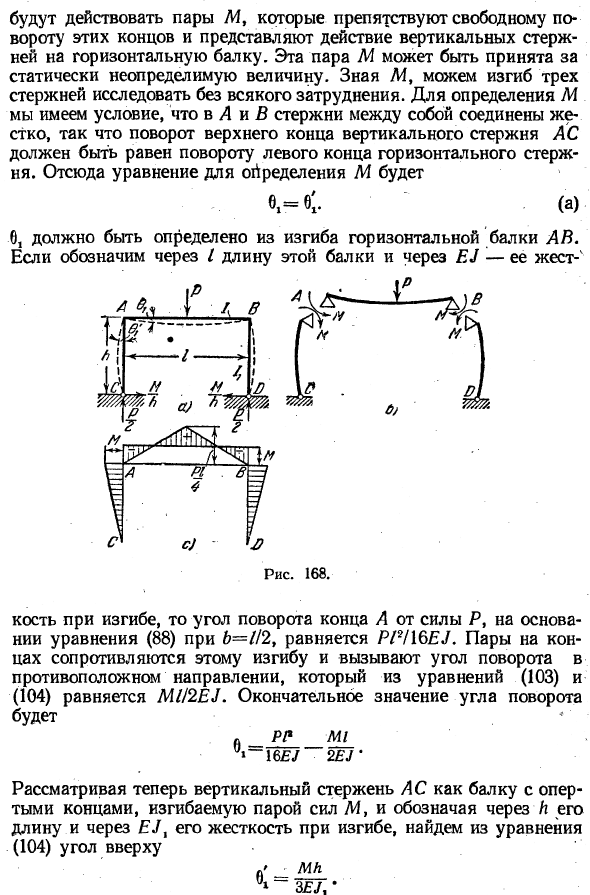
Рамка Метод, используемый для балок, статически неопределенных в предыдущем разделе, также может быть применен к раме studies. As в качестве простого примера возьмем » симметричный rdma(рис. 168)«, который имеет шарнир в C и O и нагружен симметрично.

• Вид рамы после деформации обозначается пунктирной линией.* ), Рис. 3 168, Б. если не учитывать изменение длины стержня и влияние осевой силы на изгиб стержня. Очевидно, в конце горизонтальной балки АВ * ) Одновременные операции изгиба и сжатия описаны ниже (см. Часть II).Будут работать M пар, которые препятствуют свободному вращению этих концов и представляют собой действие вертикального стержня на горизонтальную балку.

Если вы знаете M, вы можете легко изучить изгиб 3 стержней. Для определения M существуют условия, при которых стержни в L и B плотно соединены друг с другом. Поэтому вращение верхнего конца вертикального стержня переменного тока должно быть равно вращению левого конца горизонтального Rod. So, формула для определения oh M выглядит следующим образом: (ля） 0 следует определять по изгибу горизонтальной балки AB.

Эта пара, M, может рассматриваться как статически неопределенное значение. Людмила Фирмаль

Если эта длина луча и показана в ЕС — то жест-4 Рисунок 168. Кость при изгибе, а угол поворота конца а от силы Н, исходя из формулы 6 = / / 2 (88), равен ППl6EJ. Пара двух концов сопротивляется этому изгибу и вызывает угол поворота в противоположном направлении, равный уравнению (103) и (104) для M // 2EU. Конечным значением угла поворота является P / 1 M1> — 16£ / 2EJ ^

Рассмотрим вертикальный стержень как балку с опорным концом, оба конца которой отогнуты при 1 наборе усилия м, обозначенном его длиной и изгибной жесткостью EJl, из Формулы (104) получается угол вершины, а при вставке в формулу (а) длина стержня равна длине основания.、 МХГ. СТР. W7. т. 2EJ Откуда? 1. тт. LL R1. М8. (ОТ） 1 +ТТ、

Это абсолютное значение Mch, и его направление показано на рисунке. 168, b. как только вы знаете M, вы можете построить изгибающий момент, как показано на рисунке. 168., р. Вы также увидите реакции суставов С и о(рис. 168, а).Вертикальные компоненты этих реакций из условий симметрии равны друг другу, и каждая из них равна P / 2.

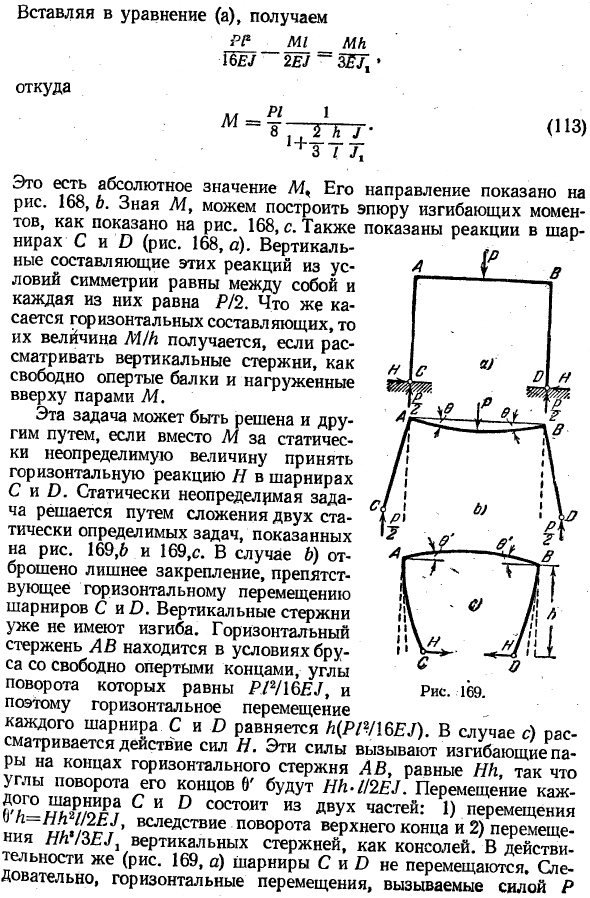
• Для горизонтальной составляющей вертикальный стержень считается свободно опорной балкой, и если нагрузка приложена к вершине парой М, то получается ее величина м / и. Я… Так… Эту проблему можно решить и другим способом. Если вместо M в качестве статически неопределенного значения принимается горизонтальная реакция соединений C и O, то статически неопределенная задача решается путем добавления 2 статически определимых задач, как показано на Рис. 2: 169.6 и 169, p.

В случай b), ненужная фиксация отбрасывается, горизонтальное перемещение шарнира C предотвращается, а вертикальный стержень не сгибается. Горизонтальный стержень АВ находится в состоянии балки со свободно опирающимися концами, угол поворота которой равен P12 / 16E/, так что горизонтальное перемещение Все петли равны C и H (P1Y \ 6E/). в) корпус, мощность I. 

Эти силы производят изгиб пары, равной NI на конце горизонтального стержня AB, и угол поворота конца 0 ’становится Hh ^ ll2EJ. Каждый шарнир C и o перемещения состоит из 2 частей: 1) движение 6 ′ / 1 = / / A2 / / 2E./ , для вращения верхнего конца, 2) движение Hh.^ / Консольный вертикальный стержень BEJ1.In факт (рис. 169, а), суставы C и£не двигаются.

Таким образом, горизонтальное смещение вызвано силой Р (рис. 169, б), силой самости (рис. 169, в), т. е. м II Нм, ял * 16NU 2EJ + W [9 Откуда? 1 П1 1 н. ТТ 1 + АА1 ′ г + 3 я / я Обратите внимание, что JL = L1, и вы можете видеть, что результат согласуется с уравнением (113) выше. Этот последний метод анализа особенно подходит для несбалансированных нагрузок, как показано на рисунке 1. 170.Капля.

Неподвижный шарнир предотвращает горизонтальное перемещение C и d и становится в положение, показанное на рисунке 5. 170, б. очевидно, увеличить расстояние между С и О. можно вдвое! Людмила Фирмаль

Угол 6.И найти увеличение этого расстояния, используя формулы (o8) и (89), умножив n на сумму 0Ж. ГRS([-С’) Рс (1-е) (21-с)] [ЫEJ] Номер Pc (1-s)H * 2EJ Правильно, он должен быть разрушен горизонтальной реакцией I(рис. 169, в).

Затем, используя результаты, полученные в предыдущей задаче, определите следующую формулу: 0 / РЛ * / РЛ * \ ПК (/- р)р \ .2£ / 1 2EP Откуда? ПК(1-s） (114） Я… 」 2 года ’• 1. имейте решение к одной концентрации, поэтому вы можете легко рассмотреть другой случай нагрузки луча рамки АВ, используя метод добавления действия силы. Теперь рассмотрим раму, которая прикреплена асимметрично к неподвижным стойкам, как показано на рисунке 1. 171.In в этом случае каждая опора имеет 3 реактивных элемента, а система имеет 3 статически неопределенных elements.

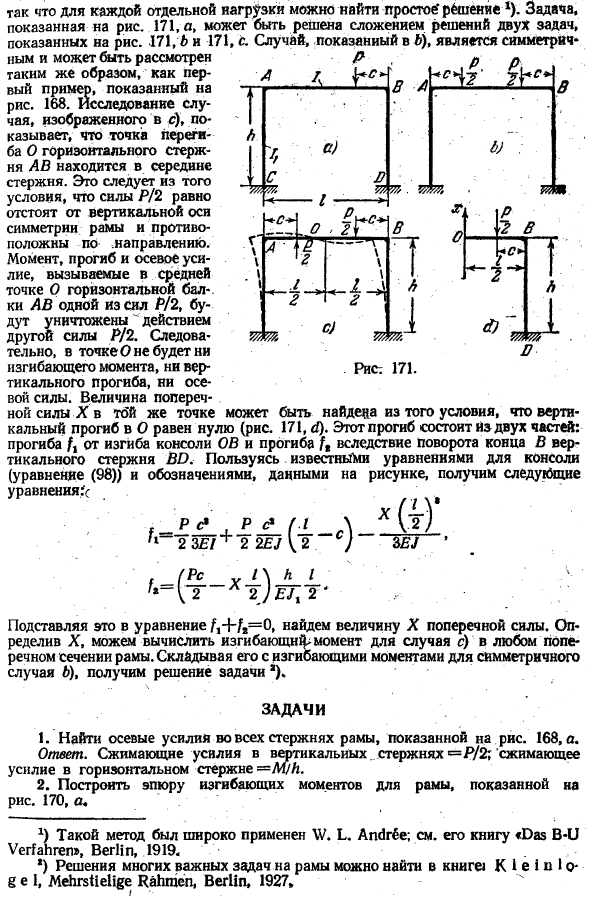
To для решения этой задачи мы будем использовать методы, основанные на методе сложения сил. Таким образом, вы можете разделить эту систему нагрузки на части и найти простое * решение*) для каждой отдельной нагрузки. Задача показана на рисунке. 171 a может быть решена путем добавления решений к 2 задачам, показанным на рисунке. .171, В и 171.п. б) показанный случай in.

Это является симметричным и может рассматриваться так же, как и первый пример, показанный на рисунке 1. 168. в) исследование нарисованного случая показывает, что точка перегиба O горизонтального стержня AB находится в середине стержня. Эго получается из условия, что сила Р / 2 равна вертикальной оси симметрии каркаса, а направление противоположно.

Момент, отклонение и осевая сила, создаваемые в средней точке O 1 горизонтальной балки AB из силы P / 2, разрушаются действием другой силы P / 2.Поэтому в точке О изгибающий момент, вертикальное отклонение и осевая сила не возникают. Величина боковой силы X в этой же точке может быть найдена из условия *, где вертикальное отклонение O равно нулю(рис. 171, г).

Это отклонение состоит из отклонения от изгиба консоли OB/и 2 частей отклонения ft при вращении конца B вертикального стержня BD. Используя известные уравнения консоли (уравнение (98)) и обозначения, показанные на рисунке, получаем следующие уравнения: Рисунок 171. * ©• УЛ (±- С）- P (A 2 2EJ \ 2.） 3EJ 2 3ЕИ. Л2 ) Ex2l Подставляя это в уравнение/,+ / * = 0, получаем значение x боковой силы.

После определения X можно рассчитать изгибающий момент корпуса c) при любом поперечном сечении рамы. Симметричный случай б) добавление изгибающего момента дает задачу а) решение. Задачи 1.Найдите осевое усилие всех стержней рамы, которое показано на рисунке. 168 а. ответ. Сила сжатия вертикального стержня= Р / 2; сжимаемость Сила горизонтальной штанги= М / Н 2.170 построить график изгибающего момента рамы, показанного на фиг. * ) Этот метод works. L. It широко использовался Андре.

Смотрите его книгу «Das B-U Verfahren, Berlin, 1919». * ) Решение многих важных задач с рамкой находится в книге* K 1 e n Io* gel, MehrstieÜgeRahmen, Berlin, 1927, вставляя значения в эти уравнения l_Rs(1-s) M1 2£Y 2EJ ’ MI million ’3£Y, 6£Y4 * МИЛЛИЛИТР 6EU4 3£Y、* Є ’ 2EJt 1 т. 6.£Год、* 次に 、 式 (b)、© （（φから φ） 、 、 式 (B), © и (φ か、 (ми)） Я Л ^ == » < 7 / 211t4-20 20 2t4-3 7 тонн М. 60 2t4 * 3 ’ Получаем 2 уравнения для определения Л1 и Мх. 8.

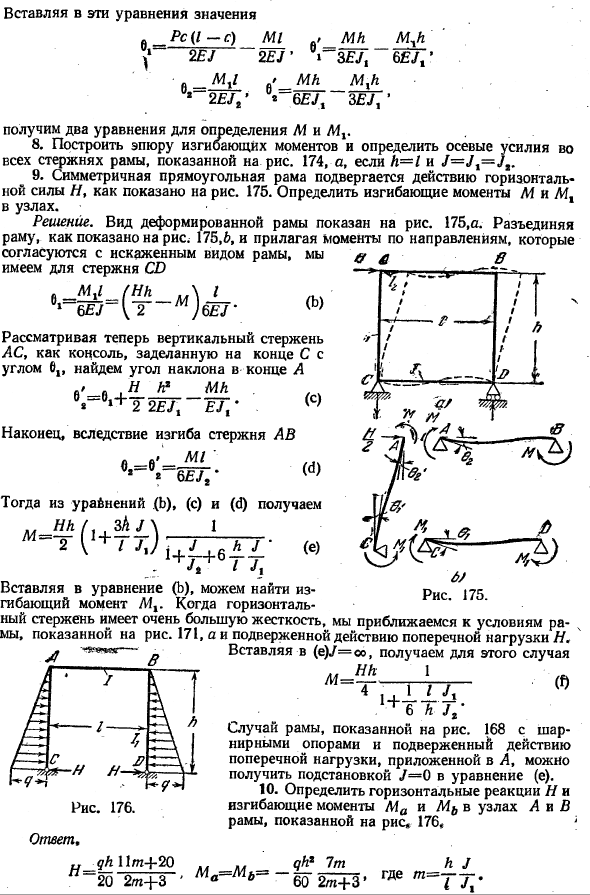
Постройте график изгибающих моментов всех стержней в раме, показанной на рисунке, и определите осевую силу. 174, a, Λ= / и V = V1 = V1. 9.As показанная на фиг. 9 симметричная прямоугольная рама подвергается действию горизонтальной силы/ 7. 175.Определите изгибающие моменты M и Mx узла.

Решение. Вид деформированного каркаса показан на рисунке. 175, a. отделите рамку, как показано на рисунке. 175.6, и применить момент в направлении, совпадающем с искаженным видом кадра、 У нас есть для стержня И МХ1(ХК \ Я 1 W-2) W ’ Если рассматривать вертикальный стержень препарата в виде герметичной консоли под углом 01E в конце С, то можно увидеть угол наклона в конце А. А— л-ч ^ МК я… 、+ 2 2£/、£/、 ’（）

Наконец, сгибая стержень AB О. Если вы вставите его в уравнение (b), вы можете найти его на рисунке 175 Изгибающий момент M1.Если жесткость горизонтального стержня очень высока, то приближаются условия работы, которые показаны на рисунке. 171, и боковые нагрузки N если вставить (e) V =ω, то получится в этом случае m NN 1 Вт M = 1-GT7—(0 1-4 — Денпасар.11. ^ 6 AU、*

В случае рамы, показанной на фиг. 168, которая снабжена шарнирной опорой и подвергается действию боковых нагрузок, приложенных к А, может быть получена путем замены V = 0 в Формуле(Е). 10. Определить горизонтальную силу реакции H и изгибающие моменты Ma и M в узлах A и B каркаса, показанного на фиг. 176. А, где М = Т7. я. ’, ’Л Ш НЛ + 6tt; 11.

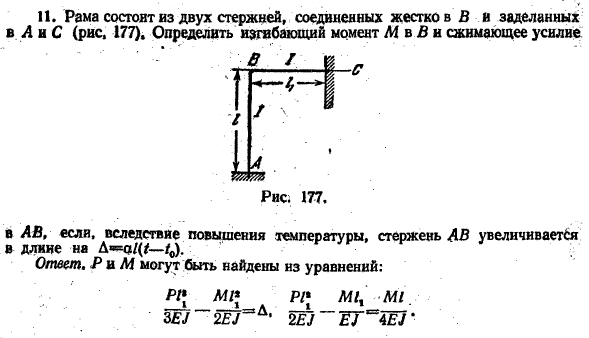
Рама выполнена из 2 стержней, плотно соединенных с B и встроенных в Annc (рис.177).B определить изгибающий момент M и силу сжатия / Л. Рисунок 177. В случае применения препарата, когда длина стержня АВ увеличивается на D * = o / (/- /0)за счет повышения температуры. Ответ. P и M можно найти из уравнения.

Смотрите также:

Учебник по сопротивлению материалов: сопромату

Балки на трех опорах	Балка, заделанная одним концом и опертая другим
Неразрезные балки	Балка с двумя заделанными концами