Определение прогиба свободно опертой балки графоаналитическим методом

Определение прогиба свободно опертой балки графо аналитическим методом

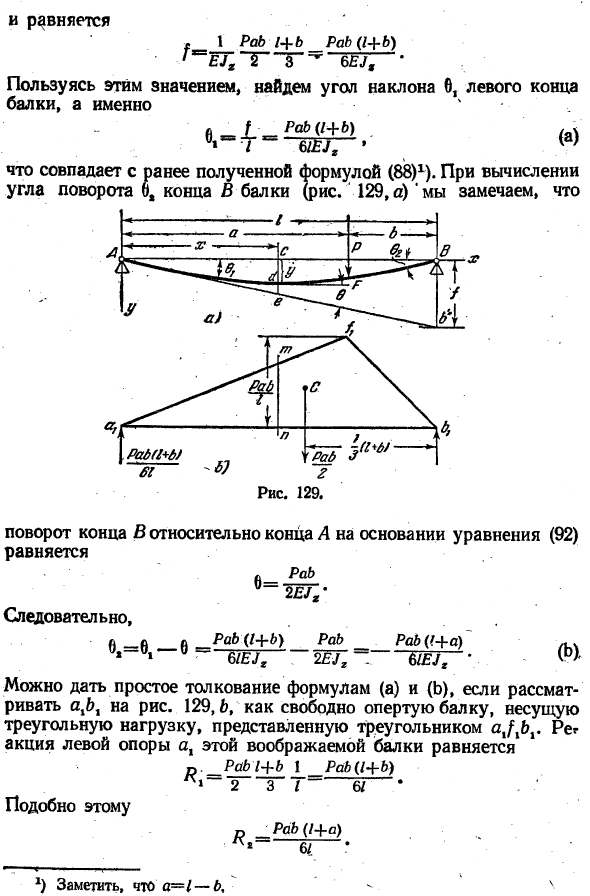
Определение прогиба свободно опирающихся балок методом графического анализа Рассмотрим случай свободно опирающейся балки с нагрузкой, приложенной к точке T7 (рис.129).Диаграмма изгибающего момента Треугольник aXbx (x (рисунок 129.6).Его площадь равна, его центр тяжести C находится на расстоянии от вертикали и pi B. О 

• Вертикальное расстояние / конец линии B-AB, которая является касательной к оси кривой A, выводится из Формулы (93). Равный 。 1 па б л + б па Б(1 + б） rX = EJx T-3 ^ 6EJ、 Используйте это значение для нахождения угла наклона b, левого края балки, то есть 4*. =(ля） 7 6 / £Oh•»

Она совпадает с ранее полученной формулой (88) 1).Когда рассчитывать Угол поворота 6, конец балки B (рис. 129, а)’ Вращение концу Б до конца, а на основе формулы(92)、 Па 6 = 2 EJt9 Так… В паб(л + б) па Раб(?+ Ля） 0, −0, 0 эВ： 6 / ЕС, в W7-6 /£7г * ^ Если рассматривать axbx фигуры, то можно дать простую интерпретацию формул (А) и (Б). 129a, B, ajxbx как свободно поддерживаемая балка, поддерживающая нагрузку треугольника, представленного треугольником.

Левая опора на 1 долю этой воображаемой балки равна R. PaY + b 1 Pab(l + b)2 3 / » 6 / Подобный этому Хао (/+а) 6 /. * ) Примечание-1-б При сравнении этих результатов с выражениями (а) и (Б) можно сделать вывод, что, разделив боковые силы на краях виртуальной балки a1b1 на изгибную жесткость EJg, получим 6 и bx на краях реальной балки AB.

Виртуальный луч (axX) называется фиктивным лучом. -* Чтобы вычислить угол наклона с любой точкой согнутой оси (рис. 129, О), необходимо вычесть угол b между касательными A и d из угла bx на опоре. Используйте формулу (92) для вычисления угла 0 из рисунка. 129.6 ′ ^ = 9,-6 = — да, Миннесота). Первый член в скобках представляет реакцию нагрузки этой балки на левую боковую опору манекена балки axLxx и левую сторону 2-й поперечной балки mn.

Таким образом, представление в скобках представляет собой боковую силу поперечного сечения TP фиктивной балки. Людмила Фирмаль

Поэтому угол наклона действительной балки в точке d можно получить путем деления поперечной силы соответствующего сечения фиктивной балки на изгибную жесткость EJ. Если принять во внимание отклонение y в точке d, то это видно из диаграммы. 129 а Что? г = се-зы. (с） Из треугольника Асе а = 8,*=!(φ Здесь/?1-реакция левой опоры воображаемого луча.

Член 2 в правой части уравнения ©выводится из уравнения (93), представляющего собой расстояние от точки оси кривой<1 до касательной Ae. И… 2 х (1е = £Г (Зона Aahtp) г.(Е)） Когда формулы (b) и (e) подставляются в Формулу ©、 (*!* — M.& Ahtp〜). ..(Да Мы видим, что представление в круглых скобках представляет изгибающий момент в поперечном сечении MN фиктивной балки.

• Таким образом, прогиб в любой точке свободно опирающейся балки получается путем деления изгибающего момента соответствующего поперечного сечения фиктивной балки на изгибающую жесткость EJZ. Подставляя в уравнение (0 значение и внимание к нему А• * и* Площадь (\ahtp =это уравнение совпадает с уравнением (86), которое ранее было получено интегрированием дифференциального уравнения оси кривой.

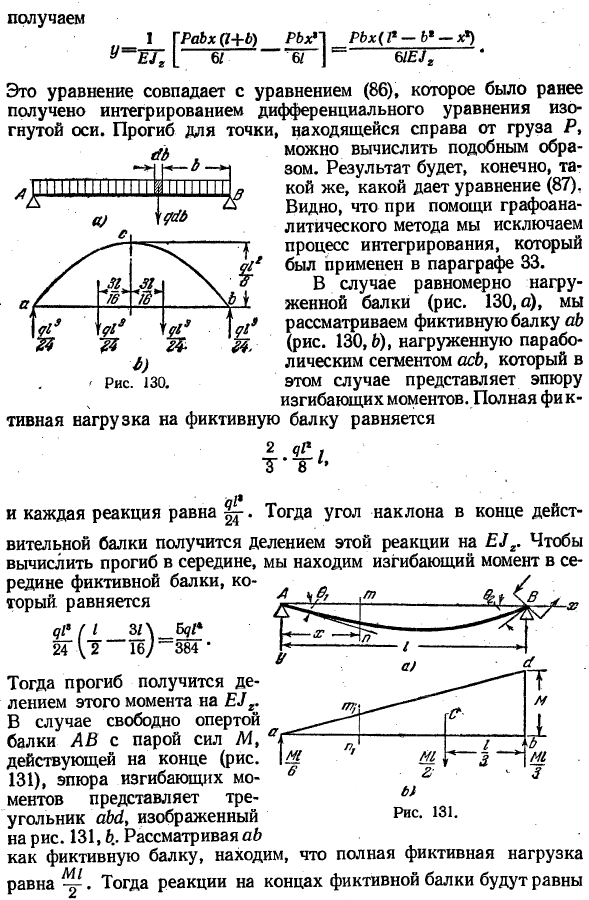
Отклонение точки вправо от нагрузки P gffi in можно рассчитать аналогичным образом. ’1 второй 1.11.1111! 11 III II1 III 1II А 0 \ фдб Мы получаем 1> 6 * П Пх(П-ВХ-х *） 6/1-6/17 ^ 1 [мини-АТС(1 + б） Зом. Конечно, результат будет таким же, как и результат, заданный формулой (87).

Вы можете видеть, что метод анализа графиков используется для исключения процесса интеграции, примененного в разделе 33. И Из \ Jl> 6 ′ / г £/〜 qi *(1 зарплата fy / 4 24В? 16/384 Далее этот момент делится на EJ и получаются прогибы. Для свободно опирающейся балки АВ с парой сил м, действующих на торцы (рис. 131), фигура изгибающего момента представляет собой треугольник abd, показанный на рисунке ab. 131.6 .. комментарий АБ В качестве фиктивной балки вы обнаружите, что общая фиктивная нагрузка〜есть.

Реакция на обоих концах фиктивного луча будет одинаковой. Людмила Фирмаль

Поэтому угол поворота кромки собственно балки равен И затем (ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ） — SHG9 *(104） год’ отклонение поперечного сечения балки ТП получают путем деления изгибающего момента соответствующего поперечного сечения балки-манекена на EJi. 1(Шу М1 ХГ х \ _ M1x /.Х * \ » лсч Г Е / де * 2 П С) — В1 НГ ПУ™в）

Задачи .1.Определите угол поворота концевых участков и прогибы под нагрузкой и в середине балки, как показано на рисунке. 132. Т. ПЕРСОНАЛЬНЫЙ КОМПЬЮТЕР. Д. * Рисунок 132. Г.»？- 1вв Л 1. \ П. в. Рисунок 133. 2? Решение.Фиктивный Луч будет иметь трапецию a (1eB, площадь Pc {1-c).

Углы поворота на обоих концах являются — 8-1 ПС(1-с） С, — ^®» — Е / Г 2 Отклонение нагрузки равно 1ГЯс2 (/- с) РС*слрс * (1 2 2 2 3] £23 < Т Центральное отклонение формулы (91) 4-я 2.Определите угол наклона касательной на конце балки, который показан на рисунке. 92. ‘\4г 7hp для(ю \ _ 2hp для •О Ответ ,•х) Сер * 180£/ * ’ \ 0х) ха {. АДЖЕЗ.、 Где H-полное давление пучка. 3. Как показано на РНС, свободно опертая балка АВ нагружена. 133.

Найдите центральное отклонение луча и максимальное отклонение.Определите угол наклона касательной на конце балки. СТР. Йейт Хто. 4 * определите угол поперечного сечения TP, а также bb и прогиб Луч.Оба конца поддерживаются свободно ■Я% » •^ Г•〜 Пара изгибающих сил Pr phiS. 134).

Решение.На рис. 134 и в показана нагрузка на фиктивную балку.И реакция на это в 1 [L * L…..] а \ Ясб * 2 л Т.\ «5»）2 /〜* «z» 1> Б)N  | ГРССР2аРсЪ Рисунок 134. КДж 1 1.2(3 21 + Следовательно, угол поворота и b * равны тг [*( ’+!)- 4 штуки, ( -?-«）• * * 5Ш; [4-я ’ („+4)] “ 5Ш, (Т если »» б * Йоу. в ’= 9 * = §ш;- с.=^- >Если угол b меняет свой знак и отклонение находится в любом месте p 3 Вниз.

Изгибающий момент в воображаемом сечении балки m,^ ~ PaPzPx Pcx \n \ (u ^ a \ 2 m! * «*- ЦУТ-й * 1 (6 + м} — М6] 6. / Итак, уравнение оси кривой на левой стороне фактического луча выглядит следующим образом:’ a. As как показано на рисунке 135, балка изгибается под действием 2 сил.

Если точка перегиба составляет 1/3 от левой опоры, определите отношение M ^ M.Ответ. MSH ^ 2MX、 Рисунок 136. ’ c. As показанные на фиг. 2, 2 доски с различной толщиной L1 и / c перекрываются вверх и вниз для поддержки равномерно распределенных нагрузок. 136, определите отношение максимального напряжения, возникающего в каждом из них. К И I. 1. 1 Шт.

Смотрите также:

Предмет сопротивление материалов: сопромат

Метод сложения действия сил	Определение прогибов при помощи эпюры изгибающих моментов
Прогиб балок с консолями	Определение прогиба консоли графоаналитическим методом