Оглавление:
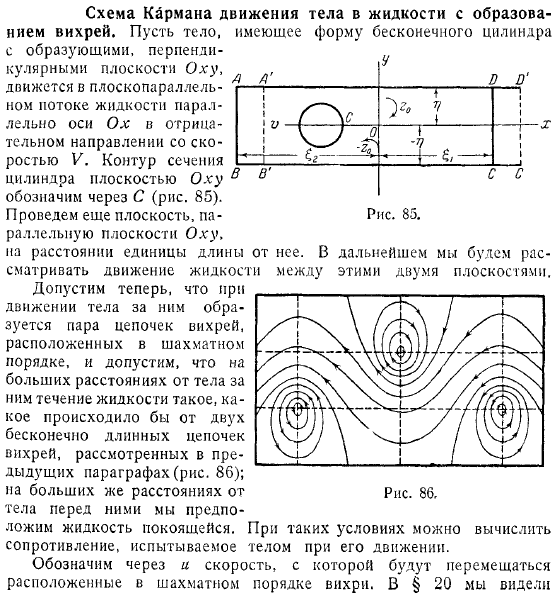



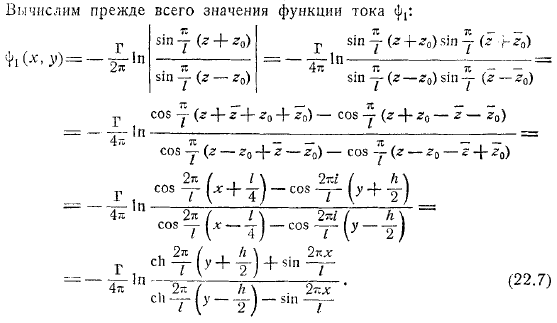



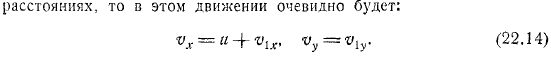

Схема кармана движения тела в жидкости с образованием вихрей
Объект в виде бесконечного цилиндра с генератором, перпендикулярным плоскости, движущийся со скоростью в отрицательном направлении, с потоком жидкости, параллельным плоскости, параллельной оси гидромеханики. Контур поперечного сечения цилиндра плоскостью обозначен буквой. Он также рисует параллельные плоскости на расстоянии единиц длины от. В будущем рассмотрим движение жидкости между этими плоскостями.
Теперь, когда объект движется за ним, образуется пара вихревых цепочек, расположенных в шахматном порядке, и на большом расстоянии от объекта за ним предполагается, что существует такой поток жидкости, который возникает из цепочек бесконечно длинных вихрей, рассмотренных в предыдущем разделе на большом расстоянии от фигуры, тела перед ними, мы предполагаем, что жидкость неподвижна. При таких условиях можно рассчитать сопротивление, которое организм получает при физической нагрузке.
Показывает скорость и скорость, с которой перемещаются расположенные в шахматном порядке устойчивости вихри. Мы подтвердили, что эта скорость равна абсолютному значению силы вихря (остальные обозначения те же). Как показано на рисунке, циркуляция верхнего вихря отрицательна. Положительная, то есть она будет. Тогда вихри перемешиваются в направлении скорости и отрицательной оси. В системе движется параллельно оси в отрицательном направлении со скоростью. Легко определить временной интервал.
- Временной интервал смещается в в интервал относительно оси это очевидно. Момента времени будут точно такими же. Единственное различие заключается в моменте между началом координат объекта и движущейся системой, то будет на больше пары вихрей, чем момент. Когда объект движется в жидкости, сопротивление создается со стороны объекта. Нас интересует устойчивость вихревых цепочек Кармана только сопротивление, то есть компонент силы сопротивления вдоль оси. Ставится задача, представляющая величину сопротивления в виде и вычисляется среднее значение сопротивления за время.
В основе расчета лежит закон импульса: приращения определенного периода проекции импульса точечной системы на любую ось будут равны сумме проекций на одну и ту же импульсную ось всех внешних сил, действующих на систему за одно и то же время. В рассматриваемой системе точек возьмем объем жидкости, разделенный по времени контуром и контуром. Кроме того, мы считаем, что уравнение линии очень велико (в будущем мы переместим в бесконечность). Уравнение прямой, и опять же, можно считать очень большим. Рассмотрим движение частиц жидкости относительно движущейся системы координат, движущейся вдоль.
Измерение частоты волн, вызываемых срывом вихрей, позволяет определить скорость потока бесконтактным способом. Людмила Фирмаль
Представляет собой сложную возможность, характеризующую движение. Если взять основные вихри верхней и нижней цепей в точке, то комплексные потенциалы, возникающие из вихрей обеих цепей, имеют вид: кроме того, к системе координат, скорость на оси для чего было сообщено, что параллельно каждой частице жидкости прибавляется скорость и параллельно оси. Соответствующий интеграционный потенциал выглядит следующим образом: потенциал определяется по.
В этом случае, согласно вышесказанному, вдали от тела, в области жидкости перед телом (направление движения) необходимо использовать потенциал, а в области позади тела необходимо использовать потенциал. Если движение характеризуется потенциалом, то очевидно затем рассмотрим движение, определяемое потенциалом. Сначала мы вычисляем значение функции потока. Во-первых, линия потока. Вычисляет значение функции потока, которая будет нарисована.
Причем соотношение получается согласно условиям. Нахождение предела равно. Так же легко найти его давайте перейдем к расчету скорости. Проекция скорости — это выражение. На или на равенство. Вы можете решить непосредственно из. Используйте последнее уравнение. Они определяются по формуле. Не разделяет действительную и мнимую части этого выражения, чтобы найти. Следует отметить, что если абсолютное значение y очень велико, то скорость движения частиц жидкости в этом случае будет очень малой, а значит, и очень большой.
- Таким образом вычисление лобового сопротивления по Карману , в дальнейшем мы сможем игнорировать скорость движения частиц жидкости за счет комплексного потенциала, который находится, например, на прямой. Однако формула. Необходимо отметить очень важные последствия, которые вытекают из. То есть, вычислить количество жидкости в единицу времени, которое протекает через линию. Четко определяется по формуле. Таким образом, поток жидкости, вызванный вихревыми цепями, всегда будет заставлять массу жидкости течь в направлении отрицательной оси, для каждого единичного времени через прямую линию.
Очевидно, по нашему предположению, мы предполагаем, что на большом расстоянии перед телом жидкость неподвижна, поэтому масса упомянутой жидкости должна расходиться в обе стороны. То есть мы приходим к выводу, что через грани выходят в каждую единицу времени массы жидкости. Наконец, становится понятным при этом движение относительно движения жидкости, которое определяется потенциалом и осуществляется на расстоянии от тела.
Вихревые дорожки также являются причиной колебания струн в эоловой арфе. Людмила Фирмаль

