Эпюры изгибающих моментов и поперечных сил

Эпюры изгибающих моментов и поперечных сил

Рисунок изгибающего момента и силы сдвига Из приведенного выше обсуждения видно, что сила, действующая на поперечное сечение TP балки, такова, что она уравновешивает изгибающий момент M и боковую силу<2 при одном и том же поперечном сечении. Итак, значения M и<2 в любом поперечном сечении определяют величину силы, действующей на это cross-section.

• To упрощается исследование распределения напряжений балки, полезно графически представить изгибающий момент и изменение боковых сил по длине балки. beam. In на таком изображении абсцисса представляет положение поперечного сечения, ось ординат представляет значение изгибающего момента или боковой силы, действующей на это поперечное сечение, а положительное значение откладывается над горизонтальной осью.

Отрицательный-ниже оси. Например, рассмотрим самонесущую балку с сосредоточенной нагрузкой P (рис.66)*).Реакция в данном случае такова i, — = t и I.= t- Вы можете взять раздел TP слева от P9 и сделать вывод, что в этом разделе. Приятель.- (2 = — г и Yi = — х.(А）

Такие графические изображения называются фигурами изгибающих моментов и боковых сил соответственно. Людмила Фирмаль

Направление поперечной силы и изгибающего момента такое же, как и на рисунке 1. Таким образом, 63, А и 64, а являются положительными. Из уравнения (а) видно, что поперечная сила остается постоянной в части балки слева от нагрузки, а изгибающий момент изменяется пропорционально x: при x = 0 момент равен нулю, а при x = a, то есть в поперечном сечении, где нагрузка равна Ru.

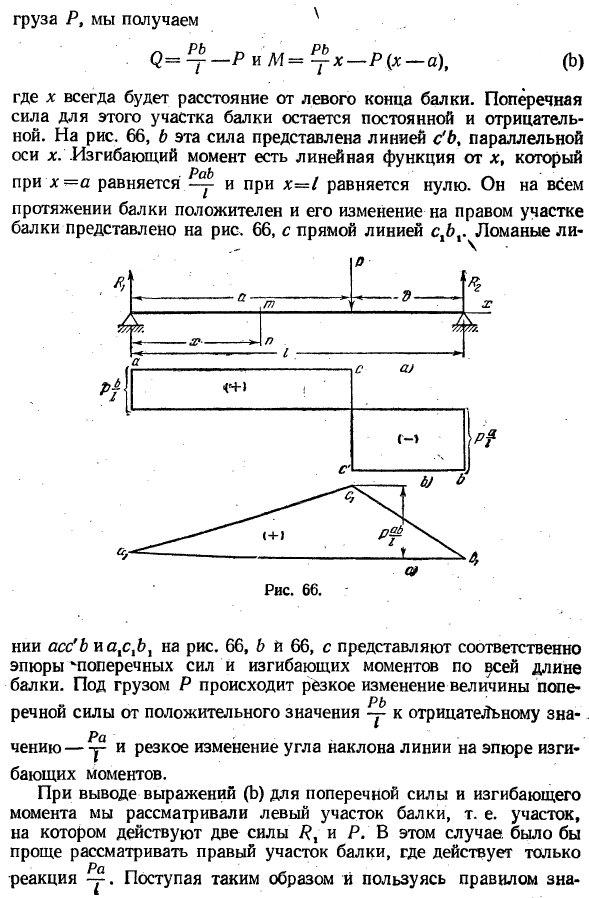
Соответствующие части диаграммы поперечной силы и изгибающего момента показаны на диаграмме соответственно. 66.6 и 66, прямая линия ac и axx. О правом поперечном сечении * ) В диаграмме ниже, мы понижаем ролик под нормальным, подвижным подшипником для того чтобы сделать его более легким. п ПБ П Д ПБ я п / ч п И М = — х-П(Х-а）、

Где X-это всегда расстояние от левого края балки. Боковые силы в этом сечении балки постоянны и поддерживают отрицательное значение. На рисунках к, в, Сила представлена параллельной линией C’B к оси X. 図６、ｂにおいて、この力は、ｘ軸に平行な線ｃ’ ｂによって表される。Изгибающий момент является линейной функцией x、 (Си） если x = a, то она равна^, а если x-1, то равна 0.Он все П?

Длина луча положительна, и изменение в правом сечении луча показано на рисунке. 66, C ^с прямой линией. ух… Л ^ О _ я х 1..(4■ / 77 £4 П с <Номер 1 С а） Г-1. И 。 м.＆ ^ (+//7 ^ ЧЧЧ./ / Р Х Рисунок 66.•＆ На рисунках Nii ass’B и ahskhl вид, bifoy toress size, C представлен вид поперечной силы и изгибающего момента по всей длине балки соответственно.

• Под нагрузкой Р величина поперечной силы быстро изменяется от положительных до отрицательных значений. резкое изменение угла наклона линии на графике р и изгибающего момента. При выводе формулы (б) поперечных сил и изгибающих моментов мы рассматривали левое сечение балки, то есть сечение, где 2 силы/и Р act. In в этом случае проще рассмотреть только правый участок балки. P(1 Реакция u. By делая это, используя правила <1 = _ * £и m — ^(1-x). (с）

Заметим, что ранее полученное выражение (b)является a-I-b, можно свести его к этой простой форме. << Это интересно отметить. Что фигура боковой силы состоит из 2 прямоугольников с равными площадями. Рассматривая противоположные признаки этих областей, можно сделать вывод, что общая площадь фигуры сдвиговой силы равна нулю.

Этот результат не является случайным. Интегральное уравнение(50）、 。 Существует G -. си.• ;«.Я… YAG=(<1） «■В А Где пределы A и B указывают, что интеграл выполняется по всей длине балки от конца A до конца B. Это нормально. Часть уравнения (b)представляет собой общую площадь участка, где P-поперечная мощность реки 1.Левая сторона такая же.

После интегрирования уравнение дает точный момент разница МВт-МА на концах B и A. В случае свободно движущегося луча, момент в конце исчезает. Поэтому ЭПУ-рис. 67.Рожь поперечная сила равна ’■Нуль. • Если на балку действует более одной силы (рис. 67), то балка делится на несколько секций, и для каждой секции (?)И М. И m * = yagh .-(ми)）

Для 2-го участка балки, ar <x < ag9、 <2 = ф? Х-я и М ^ я ^ Р%(х-Эр). (Да Для 3-го участка балки, а именно al <x < aa, удобнее рассматривать правую сторону балки, чем левую side. In в этом случае, вы получите: , 0» — (/?,- П. С.）М = /?, (/- х)-Р9 (/- -6.） Наконец, в последнем разделе»луч»、 (г） М= -•/?, М = # н: й -.(Ч.) Из Формулы (e)-g — (h) видно, что боковые силы остаются постоянными в каждом сечении балки.

Изгибающий момент каждой секции балки является линейной функцией x Людмила Фирмаль

Таким образом, фигура боковой силы получается как, как показано на рисунке. 67, 6.. So, в соответствующем сюжете сюжета он представлен косой прямой line. To проведя эти линии, из формул (e) и(h) мы увидим, что на краях пучка x = 0 и X = /момент равен нулю.

Момент под нагрузкой получается путем подстановки формулы (эмо и*(h), x = al9 x * = at и x-a, respectively. So, для вышеуказанных моментов получаем следующие значения: М = Rxav м = P9ag-РДА — а), м = RJb9. Используя эти значения, можно легко построить график изгибающего момента, как показано на рисунке. 67, стр. В практических приложениях важно найти максимальное или максимальное сечение изгибающего момента. Низкое значение.

Для сосредоточенной нагрузки, описанной на Рис. 1. 67, максимальный изгибающий момент происходит под нагрузкой Рг. Эта нагрузка соответствует изгибающему моменту » точка dt%», где тангенс угла наклона диаграммы меняет знак на diagram. In кроме того, из Формулы (50) видно, что касательная угла наклона фигуры изгибающего момента в любой точке равна боковой силе.

Поэтому изгибающий момент будет максимальным или минимальным значением в той части, где изменяется боковая сила 8нак. Если поперечная сила по длине балки изменяется от положительного до отрицательного значения, например, при нагрузке Pt на фиг. 5, 67, то тангенс угла наклона диаграммы изгибающего момента также изменяется от положительного до отрицательного.

Поэтому в этом сечении существует максимальный изгибающий момент. Изменение Q от отрицательного значения до положительного указывает на минимальный изгиб moment. In в общем случае фигура боковой силы может пересекать горизонтальную ось в нескольких местах. Далее такие пересечения соответствуют соответственно максимуму или минимуму фигуры изгиба moment.

To найти максимальный изгибающий момент численно, нужно изучить численные значения всех этих максимумов и минимумов. Теперь рассмотрим случай равномерно распределенной нагрузки(рис. 68).Из предыдущего рассуждения(стр.） Для поперечного сечения, расположенного на расстоянии x от левой опоры、 М =? (§- •) И M =((1-х). (Я）

В этом случае можно видеть, что фигуры для боковых сил представляют собой прямую линию с наклоном в продольных координатах: x = 0 и x=/. 68, B, что равно^и -соответственно, как показано на рисунке. От Формула (i) в этом случае изгибающий момент ver — ^(rtgptitp〜PT) представляет собой параболу tt’pigptpttp, в центре которой находится вертикальная ось Пролет балки (рис. 68, с).

Моменты на обоих концах, то есть x = 0 и x=/, равны нулю, момент имеет максимальное значение в центре пролета, а боковая сила меняет знак. Это максимальное значение получается подставляя x-y в формулу (i)、 М= * — • / Vimax 8 * Если равномерная нагрузка q охватывает только часть пролета (рис. 69), то 3 участка длины a должны рассматриваться отдельно. b и c. Rt и определить реакцию? замените рав таким же образом, аспредёред, пелелелел.

Результаты QB нагрузки. «Из уравнения статики моментов для B и-A、 Боковая сила разгруженной левой части балки и изгибающий момент(0 < x <o)、 Г = /? И М-Р ИКС. (Дж） В случае поперечного сечения mn, взятого в нагрузочном сечении балки, сила поперечного сечения получается вычитанием нагрузки q (x-a)\из реакции? Он расположен в левой части этого раздела.

Изгибающий момент того же участка получается путем вычитания момента нагрузки на левой стороне этого участка из реакции moment. So я все выясню. М = РЛ-м(х-A)и М = RLX может-Г(Х-а)^ -^ -. (к）Правый участок балки без нагрузки, с учетом правой силы любого участка、 И-(1） Используя уравнения 0, (k) и (I), можно легко построить график сдвиговых сил и изгибающих моментов.

Диаграмма поперечной силы (рис.69, б) состоит из горизонтального сегмента оси, который соответствует ненагруженной части балки, и наклонной линии, < cx & x>, которая соответствует равномерно нагруженной части. — я. ..• Т-ПГ. МП IM 11.11 III V f г.* Лу. б. th. * (Рисунок 69, с) 2 заштрихованные линии arsr и brk» 1 Кривая с вертикальной осью, соответствующей нагрузочной части балки. Максимальный изгибающий момент в точке ех.

Это соответствует точке ех>, где боковая сила меняет знак. В точках С1 и параболы, наклонных линий Ayacr и c1r2r связались, соответственно, это получается из-за того, что на рисунках боковых сил в точках с и<2 нет резкого изменения величины боковой силы. Так… Рисунок 69.

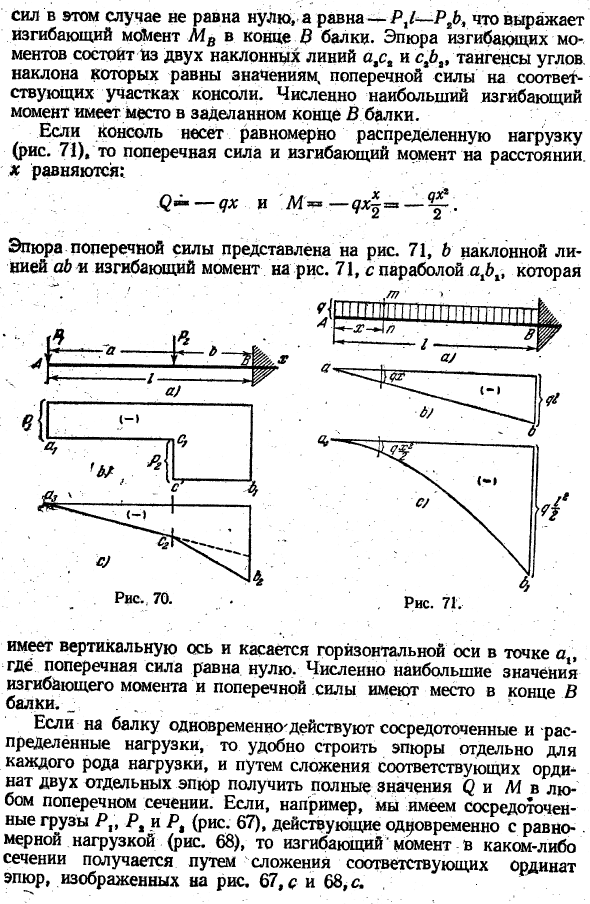
Исходя из Формулы (50), нет резкого изменения наклона изгибающего момента предвестников в соответствующей точке. ж / д-и Для кантилевера (рис.70) используйте тот же метод для создания фигуры с той же боковой силой и изгибающим моментом, что и для лежащей балки. Измерьте x от левого края балки и исследуйте область слева от нагрузки P (0 •’•; * в Я…

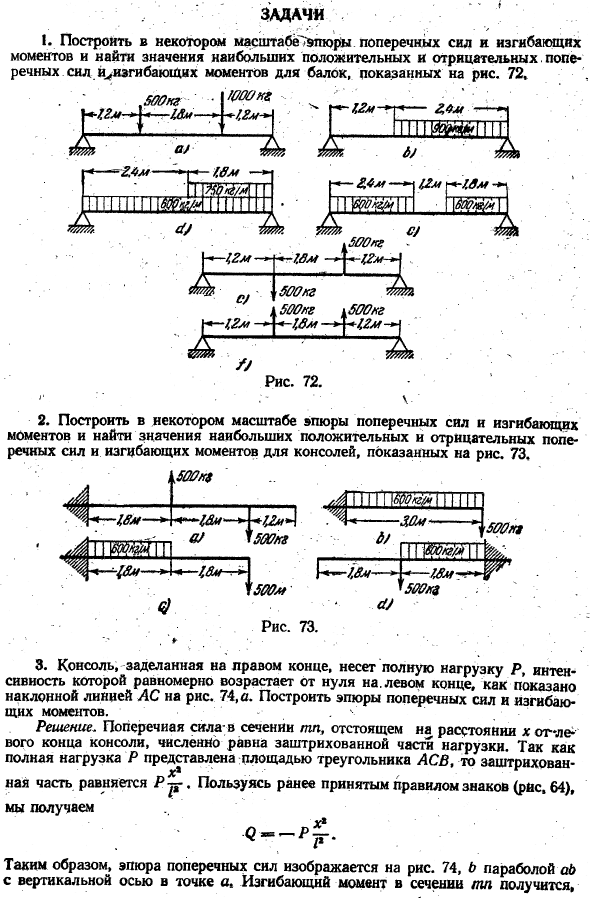
В определенном масштабе построим изменение боковой силы относительно изгибающего момента и найдем значения максимальной положительной и отрицательной боковой силы и изгибающего момента балки, показанные на рисунке. 72.、 Шао Куо 500кг Вт- ч. 4 м. И-Іііііі* 1 || ＆ 1. ^ д / 2.4 м — ► ’ Ш [12М г * −7.виртуальная память 1. 1 шт 5о0кгно. / 24М… г. /.Ом. например: ’КК / м Один. 1ШР. 1М. / — 7,6 М-Д. — с. / г -/, 2М — <б-ин■э-. 56. Здесь. Г / / 77 / Л 500кг. 500кг. Iyyokg K500kg 12m | — 7, ВМ-72М Что?/ Рисунок 72.

2.Создайте конкретную масштабную диаграмму поперечных сил и изгибающих моментов и найдите значения максимальных положительных и отрицательных полей «речных сил и изгибающих моментов» консоли, показанной на рисунке. 73. 50кг. — «А + 12м4» ТС-я- <И 500кг. Хромой. 500кг. ] $ Ыб ’/ * — 7лм. 5. / shshlp [±7] — да. я-и -/. 7,5 м. 500кг. 500м рисунок 73. «У» ч> 3.На консоли, герметизированной с правого конца, имеется полная нагрузка Р, интенсивность которой равномерно возрастает от нуля.

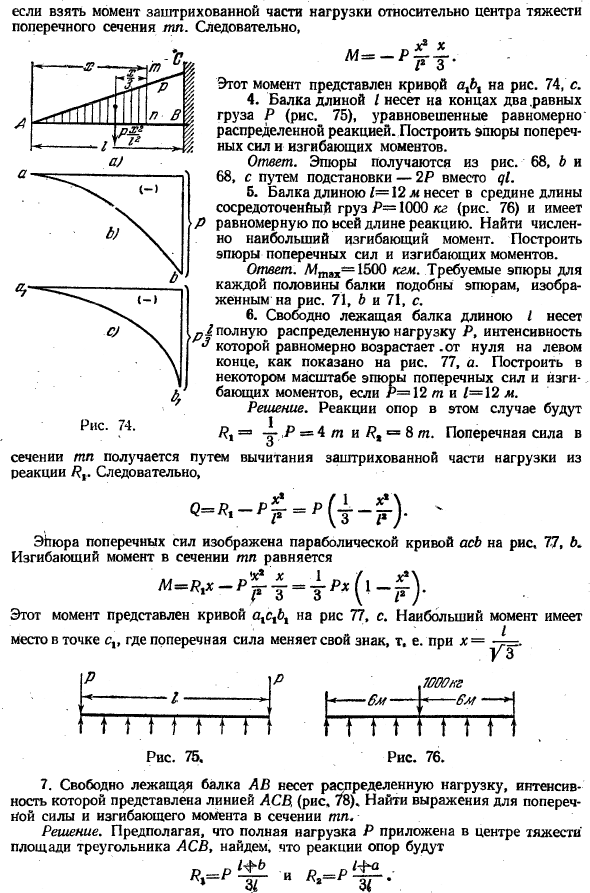
График левого края 74, L боковая сила и изгибающий момент показаны штрихами динамика на рисунке. — 4. Решение. Расстояние консоли x og * le *боковые силы сечения m, разнесенные по концам, будут численно равны затененной части нагрузки. Полная нагрузка P заштрихована, потому что она представлена областью треугольника AC B икс * / 5-я часть равна R. используя условности ранее принятых знаков (рис. 64)、 Мы получаем Xa * — РИТЭГ-

Итак, диаграмма силы сдвига показана на рисунке. 74, точка B с параболой ab с перпендикулярной осью к с, изгибающий момент сечения mn При принятии момента штриховки части груза относительно центра тяжести секции mp. So … ВА Х м = п£т Диаграмма 74. Этот момент представлен на рисунке кривой axbx. 74, С. 4.Балка длиной l отвечает за 2 равные нагрузки P (рис.75) на ее концах, а равновесие удерживается равномерно распределенным противодействием.

Построить график боковых сил и изгибающих моментов. Ответ. Сюжет получается из рисунка ’ 68, b и 68, вместо замены Path-2?/. а. балка длиной l = 12 м имеет сосредоточенную нагрузку P = 1000 кг в середине длины (рис. 76) и имеет равномерную реакцию по всей длине. Найти численно максимальный изгибающий момент. Построить график боковых сил и изгибающих моментов.

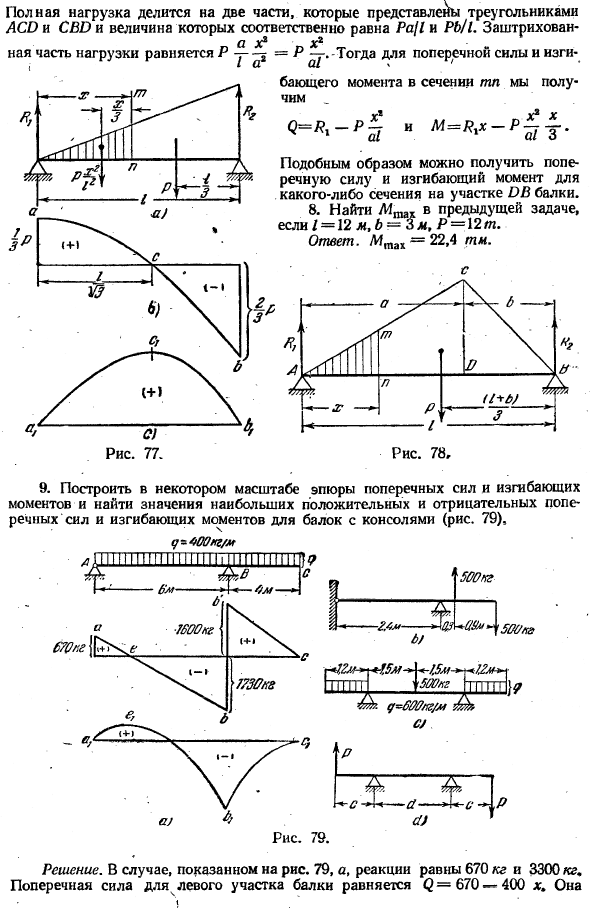
Ответ. Пользователь (ы), которые смотрели Mt9X — 1500 человек. График, необходимый для каждой половины балки, аналогичен графику, показанному на рисунке. 71, б и 71, стр. 6.As показанный на фиг. 1 отдельно стоящий пучок длиной I передает Р1, и интенсивность его распределения 3 равномерно возрастает. 77, a. для £ = 12 м и/ = 12 м создайте конкретный масштабный график боковых сил и изгибающих моментов.

Решение. Реакция поддержки в данном случае такова / ?, = — o * P = 4 t и = 8 t. боковая сила Сечения ТП получается путем вычитания заштрихованная часть нагрузки от реакции так У ЭУРа от поперечных сил показана на рис. 77 параболических по АСВ. Изгибающий момент профиля tp М. 

Этот момент представлен 77-й кривой axxxx. Максимальный момент возникает в точке СХ, где боковая сила меняет знак М. То есть, Х — > р=. 7000кг-ом 600. GTTTTT Диаграмма 75、 компания GTT. компания GTT. Рисунок 76. 7.Автономная Балка A B несет распределенную нагрузку, представленную линией ASV. (Рисунок 78), найти формулу для поперечной силы и изгибающего момента поперечного сечения Мп.

Решение. Предполагая, что максимальная нагрузка P приложена к центру масс в области треугольника ASV, отклик опоры равен: 1 * b 3 * И затем с. / / ?, » / > Общая нагрузка делится на 2 части и представлена треугольниками ACD и CBD, размеры которых составляют Pa / 1 и Pb / 1 соответственно. С тенью- д йф * ■ ДС * Большая часть нагрузки равна Ру ^ = р -.Затем о поперечной силе и изгибающем моменте поперечного сечения ТП、 Г = ГХ-и M = rxx в-п-л-Дж.

Таким образом, можно получить боковые силы и изгибающие моменты для любого сечения в сечении ДБ балки. 8.Найдите UI™в предыдущей задаче. Часов%= 1 = 12 м, б-5 м, п-12т СП 1+ » ответ. Mtz1 = 22,4 ТМ T% ✓1> / 77 ′ ПВЛ п, п (■И>％ 1 1 x f Ю\ 6.）\ СиДжей. \ Рисунок 78.、

9.Составьте конкретную масштабную диаграмму поперечной силы и изгибающего момента и найдите значения максимальной положительной и отрицательной поперечной силы и изгибающего момента балки с консолью (рис.79). д-400кг / м. gptlgt gtttttttttttggt А. * АО О. В. •7000кг | . я — » 7730×8 500кг. Ноги. 1. — 400 фунтов. 5. / д = 300lg / м СиДжея г * — с Диаграмма 79 Ф ЗЕТ. Да.） Решение. Если показано на рис. 79, а, то реакция составляет 670 кг и 3300 кг, а боковая сила левого участка балки равна (2 = 670-400 х).

Она показана на рисунке диагональной линией ab. Боковое усилие правой части балки определяется, как показано на наклонной линии B * s консоли. Изгиб Мистер Си. Момент левого сечения балки равен M = 670 x-400.Он нарисован раболой 0 / Х6 6|.Максимальный момент возникает в точке Е и соответствует точке е. f где боковая сила изменяет знак.

Фигура изгибающего момента в правом сечении такая же, как и в консоли, и нарисована параболическим bxcx, который касается горизонтальной оси в точке C. • 10. 2 равные коэффициенты*(рис. 80) — длина/балок равномерно распределенной нагрузки. Найти расстояние d между опорами таким образом, чтобы изгибающий момент в центре балки был численно равен изгибающему моменту балки. support. In в этом случае постройте график силы сдвига и изгибающего момента. Ответ. <1 = 0,686 /. 、

Смотрите также:

Эпюры изгибающих моментов и поперечных сил

Чистый изгиб	Изгибающий момент и поперечная сила
Различные формы поперечных сечений балок	Зависимость между изгибающим моментом и поперечной силой