Зависимость между изгибающим моментом и поперечной силой

Оглавление:

Зависимость между изгибающим моментом и поперечной силой

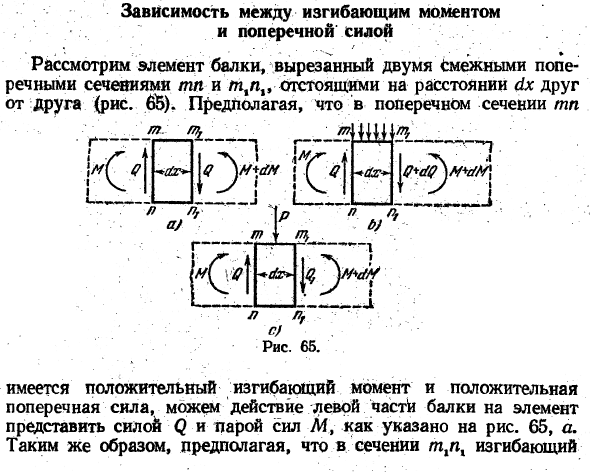
Отношение изгибающего момента. K и поперечная сила Рассмотрим элементы балки, вырезанные на 6 × 2 смежных сечениях m и m, m (рис. 65).На поперечном сечении ТП Км и др.■ * их * k \ M \ÏÏM{{и U：. Л / С а).Ю Ю Ю Ю Ю Ю. — К. «*Г1» -. — т. к. 1.- Л ЛГ.. **… •…■с） ’■Рисунок 65.

Поскольку существует положительный изгибающий момент и положительная боковая сила, как показано на фиг. 2, то усилие левой части балки на элемент можно представить в виде Силы f и пары сил M. 65A. In таким же образом, изгиб в разделе thx 2 1] зависимость изгибающего момента и боковой силы 73 — ’»’» /. ’вл «»- В •• *•. * * В — * 5″•. В.* — • ’- • • , * * * В’.Г. ;’.Ч’

Если момент и силы сдвига положительны, то действие балки на правую сторону элемента может быть представлено парой сил и усилий. Людмила Фирмаль

Если на балку между секциями mn и m, n не действуют силы (рис. 65, а), то боковые силы этих 2 секций будут равны equal. As для изгибающего момента, исходя из состояния равновесия элементов, они не равны 2 смежным участкам, а приращение изгибающего момента равно моменту силовой пары, которая представлена 2 равными и противоположными силами Q, то есть они равны друг другу. 。 ..•,,••* ••、 1•В.• юм = — (1бс и М-а… …..(50）

Так, во всех частях балки между нагрузками боковая сила равна производной изгибающего момента X. Здесь рассмотрим случай, когда распределенная нагрузка интенсивности q действует между площадью поперечного сечения mn и mnx(рис.65, б). в этом случае суммарная нагрузка, действующая на элемент, будет равна dyh. Если нагрузка действительна, то положительна q. при продувке, исходя из равновесного состояния элемента, можно сделать вывод, что боковая сила поперечного сечения txp отличается от боковой силы поперечного сечения tp.

Оттуда * В. ;- <7.. Год）_ Таким образом, производная боковой силы по отношению к x равна интенсивности нагрузки с отрицательным знаком. * * ’ Когда вы берете момент всех сил, действующих на элементы、 им => я (1х-д (1х -. Игнорировать 2-й член справа side. As малую вторичную величину, вернемся к формуле (50) и сделаем вывод, что в случае распределенной нагрузки производная изгибающего момента равна поперечной силе.

Помимо дифференциальных зависимостей существуют интегральные зависимости, получаемые из формул дифференциальных зависимостей. Людмила Фирмаль

Когда сосредоточенная нагрузка P действует между соседними участками mn и mnx (рис. 65, В), происходит резкое изменение величины боковой силы. φ обозначает поперечную силу сечения mn и < 2 сечения mnx. Тогда из условия равновесия элемента mxnx n、。 \ Я <2： В результате величина сдвигающей силы равна х)здесь вес балочного элемента игнорируется. P при прохождении через точку приложения нагрузки. Затем, из Формулы (50), происходит внезапное изменение величины, в точке действия концентрации Вода.

Эпюры изгибающих моментов и поперечных сил	Типы балок
Чистый изгиб	Изгибающий момент и поперечная сила