Изгибающий момент и поперечная сила

Изгибающий момент и поперечная сила

Давайте рассмотрим луч по желанию. Опорный конец (рис.61, а) подвергается воздействию вертикальной силы Pg, Pr, Pr. Предположим, что балка имеет симметричную продольную плоскость и на эту плоскость действует нагрузка. Затем, на основе симметрии, мы приходим к выводу, что изгиб происходит в одной плоскости.

• Поскольку Нормаль φ°Pm поперечного сечения балки симметрична в круговом, прямоугольном, I-образном и Т-образном сечениях, это условие симметрии выполняется в большинстве практических случаев. Более общие случаи асимметричных поперечных сечений описаны ниже (см. Главу 8). …

Для исследования сил, возникающих в балке при изгибе, используйте уже использованный метод нахождения сил, возникающих в стержне при простом растяжении(Рис. 1).Представьте себе, что балка AB разрезана на 2 части сечением TP, взятым на любом расстоянии x от левой боковой опоры A (рис.61, а), а правая сторона балки разрушена.

При рассмотрении оставшейся левой балансировки балки (рис. 61.6) необходимо учитывать внутренние силы. Людмила Фирмаль

Распределенные в сечении Абрамса, а также внешние силы, такие как нагрузка P и PJ и реакции. Представляет действие справа. Луч: слева. К 1 * Т 1 У-г-У7. 1. Так / Б * — Б-А;; Т /> Б) \ о Что?、- а. эээ… Диаграмма 61. Эти внутренние силы, вышеупомянутая внешняя сила Px, Pr n /?Он должен быть такого размера, чтобы он уравновешивался с R. 

Для последующего рассуждения полезно представить реальную систему внешних систем. Власть тебе.. Цервикальная эквивалентная система. Из статики нам известна система параллельных forces. It можно заменить на 1 силу, равную сумме алгебр.1 комплект питания плюс данный power. In в некоторых случаях сила может быть заменена. П пр-и/?Вертикальная сила<2, действие.

• В плоскости поперечного сечения ГПУ Пара сил М. величина силы равна. Р^, — пр-пр(а） Я… и… ’ * * И значения моментов пары сил равны;:»>.М = / 1х-Р, (:: — Си) — па(х-*).-;- (си） Сила<^, равная алгебраической сумме внешних сил, распределяется Поперечное сечение расположено на левой стороне ТП и называется поперечной силой по сечению т. пара сил м относительно центра тяжести этого сечения, равная алгебраической сумме моментов внешних сил, расположенных на левой стороне поперечного сечения Мп, называется изгибающими моментами сечения Мп.

Таким образом, система внешних сил на левой стороне поперечного сечения МП может быть заменена статически эквивалентной системой, состоящей из боковой силы<2 и 1 пары сил м, действующих на плоскость поперечного сечения (рис.61, в).Сила, распределенная в поперечном сечении TP и представляющая собой действие правой стороны балки на левую сторону, должна быть такой, чтобы она уравновешивала изгибающий момент M и боковую силу<2.

Например, рассмотрим равномерно нагруженную балку, показанную на Рис.1. 62, a. если нагрузка на единицу длины представлена d, то реакция в этом случае равна: Чтобы исследовать силы, распределенные по поперечному сечению mn, снова рассмотрим равновесие левой части балки. (Рис. 62, 6).

Если распределенная нагрузка действует на балку вместо сосредоточенной нагрузки, можно применить тот же вывод, что и в предыдущем случае. Людмила Фирмаль

Внешние силы 4. 4. т и Это очень простое и удобное в использовании приложение. * Б. ’а / т 11111 и 111111 н. •1 Что же действует на эту часть луча-реакция/?И нагрузка равномерно распределяется по длине x. конечно, результат этой последней нагрузки будет равен dx. In вывод, алгебраическая сумма всех степеней y слева от раздела ТП, равный/?,- ЦТ. Алгебра рис. 62.

Сумма всех моментов силы Реакция слева от секции Мп относительно центра тяжести этой секции, момент реакции/?, полученное вытягиванием момента результирующей распределенной нагрузки из x. момент распределенной нагрузки явно равен Х ОО * 4×2 * * 2 * Итак, для алгебраической суммы моментов выражение Все силы, действующие на левую сторону балки, действуют на плоскость поперечного сечения ТП、 -<7 * = <7（-5 — *）、（С.）

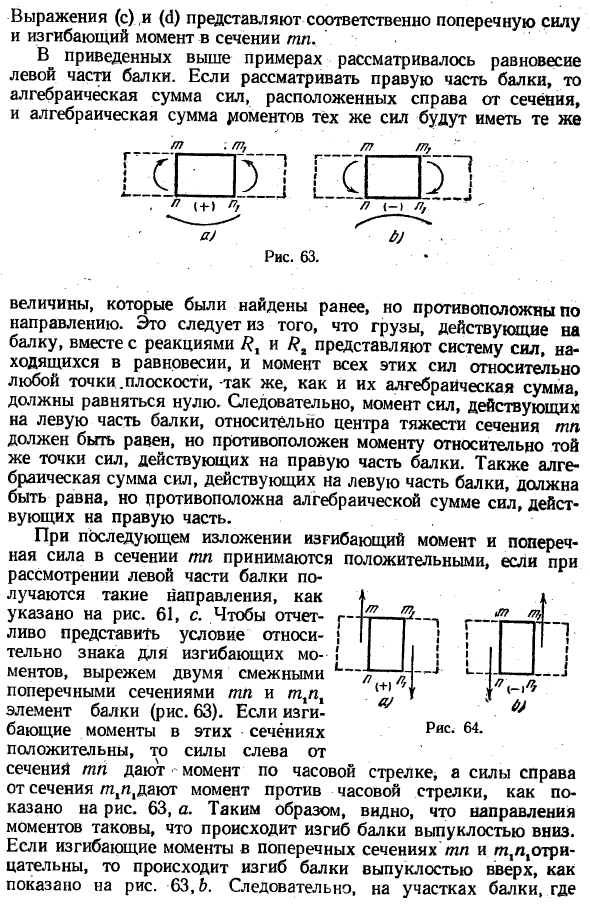
Пара равных сил М = /?, *- икс.) (СЗ）Уравнения©и (1) соответственно представляют боковые силы и изгибающие моменты поперечного сечения Мп. В приведенном выше примере рассматривалось равновесие на левой стороне балки. Рассматривая правую сторону балки, алгебраическая сумма сил на правой стороне сечения и алгебраическая сумма моментов одних и тех же сил будут одинаковыми 77. / 7 (- «л、 Л Что? W R —- ！ г 1-1 у g-1 I£; і Рисунок 63.

Количество ранее найденных но противоположных directions. Is это основано на том, что нагрузка, действующая на балку, действует вместе с реакцией? Должно быть zero. As в результате момент силы, действующей на левую сторону балки относительно центра тяжести сечения ТП, должен быть равен, но противоположен моменту для той же точки силы, действующей на правую сторону балки.

Кроме того, алгебраическая сумма сил, действующих на левую сторону балки, должна быть равна, но противоположна алгебраической сумме сил, действующих на правую сторону. Рисунок TP 61, p при рассмотрении левой стороны балки в следующем представлении. Вырежьте балочные элементы с 2 смежными поперечными сечениями mn и mnx, чтобы четко представить условия для знака изгибающего момента (рис.63).

Если изгибающие моменты этих секций положительны, то левая сила равна _ Рисунок 64. Как показано на рисунке, сечение mn дает моменты по часовой стрелке, а сечение m ^силы справа дают моменты против часовой стрелки. 63, а. таким образом, можно видеть, что направление момента таково, что луч изгибается с нисходящей выпуклостью. Если изгибающие моменты сечений mn и mn отрицательные, то балка изгибается вверх, как показано на рисунке. 63.6.Поэтому в разрезе балки、

Смотрите также:

Изгибающий момент и поперечная сила

Зависимость между изгибающим моментом и поперечной силой	Растяжение или сжатие по трем взаимно перпендикулярным направлениям
Эпюры изгибающих моментов и поперечных сил	Типы балок