Оглавление:

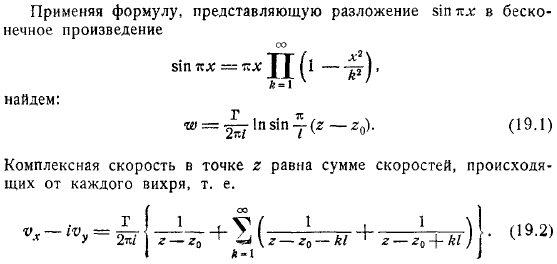


Одна вихревая цепочка
Рассмотрим бесконечную серию точечных вихрей в гидромеханике, находящихся на прямой с одинаковой интенсивностью на одинаковом расстоянии/расстоянии друг от друга. Комплексный потенциал любой точки жидкости, не совпадающей ни с одним из вихрей, равен сумме потенциалов отдельных вихрей.
- Разница был разделен была разделена на, умножается на изменить только какие-либо постоянной. Так как функция определяется с точностью кармана до аддитивной постоянной, то вы имеете право ввести, то разложение: бесконечное произведение комплексная скорость в точке равна сумме скоростей, генерируемых каждой вихревой цепочки Кармана .
Явление можно наблюдать лишь при ограниченных значениях числа Рейнольдса. Людмила Фирмаль
Используя тот факт, что скорость является производной комплексного потенциала, проще получить такое выражение комплексной скорости: где определяется уравнением. Понятно, что все вихри должны двигаться с одинаковой скоростью, поэтому достаточно рассмотреть, как движется точка, чтобы найти скорость движения самой вихревой цепи, то есть скорость каждого вихря, его компонента.
- Скорость двух вихревых цепочек в точке возникает из эффектов всех вихрей, кроме самого вихря. Поэтому в выражении должно быть включено во все условия, кроме первого. Уравнение, мы видим, что скорость вихря равна нулю, так как член сжимается попарно. Поэтому вихри и так далее работают в противоположных направлениях попарно, так что вихревая цепь остается неподвижной.
Размеры дорожки зависят от размера обтекаемого тела, при этом существует линейная зависимость между шириной дорожки и расстоянием между соседними вихрями. Людмила Фирмаль

