Оглавление:






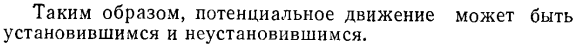

Движение жидкой частицы. Понятие о вихревом и потенциальном движении
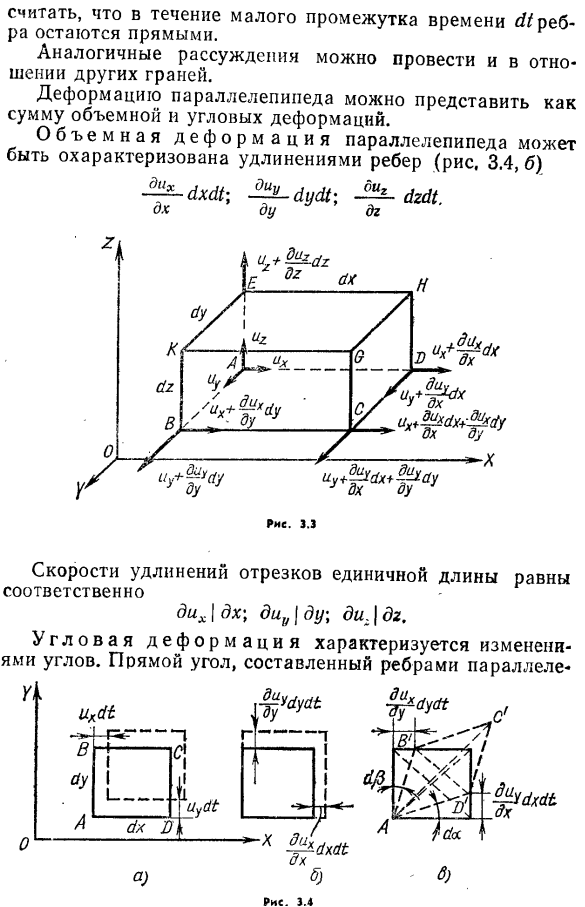
Движение жидкой частицы. Понятие о вихревом и потенциальном движении. По мере движения жидкости изменяется расположение частиц в пространстве и их деформация, то есть изменяется форма и объем. Бесконечно малые ребра, параллельные осям xx, c! Рассмотрим частицу жидкости прямоугольной формы с Y,©(рис. 3.3).Пусть в какой-то момент времени координаты I, в вершинах параллелепипедов x, y, r, компоненты локальных скоростей равны им u, u. Если в качестве полюса выбрана точка а, то поступательное движение всего параллелепипеда между моментами времени si представляется проекцией их si \ si \ si \ si (рис. 3.4, а).
Если мы предположим, что скорость является непрерывной дифференцируемой координатной функцией, мы представим скорость остальных вершин параллелепипеда через скорость в вершине L. 3.3.Используйте различные компоненты, такие как скорость в разных точках!?Лицо будет не только перемещаться в пространстве, но и деформироваться. Потому что концы параллелепипедов маленькие、 61. На короткое время мы предполагаем, что серебро остается прямым. Вы можете создать аналогичные соображения для других аспектов.
Безвихревым движение будет в случае, если вращение жидкой частицы отсутствует. Людмила Фирмаль
- Деформацию параллелепипеда можно представить как сумму объемных и угловых деформаций. Объемный вариант параллелепипеда характеризуется удлинением ребер (рис. 3.4, б) -двойника YHM; МЕ s1usI; ДГУ (, ДХ ду ДГ Скорость удлинения сегмента единицы длины равна, соответственно Диг | ДХ; Диг| ДХ; Диг / ДГ. Угловая деформация характеризуется изменением угла. Прямоугольный, состоящий из параллельных ребер Трубчатые AB и AO плоскости 62 COW изменяются с суммой углов da \ c1 $по мере движения жидкости(рис. 3.4, c). Да. д._ dh. ых ■<и Йоу. три пьесы. ЦТ. ’МКС.
Угол сдвига между осью OX и краю Ау、 И угол сдвига между осью OS и стороной AB До 4 к Далее, угловая деформация (деформация сдвига) ’ Да+ м + ^ д(. ДХ делать. Отношение угловых деформаций в плоскости Хоу ГФ-\〜ГФ yoiu, МГП (ЦОР делать Получить угловую скорость деформации плоскостей U02 и X01 соответственно Диу, копать> Диг, Диг ДГ ду ДГ ДХ Угловая скорость деформации обычно выражается следующим образом: ОГА = и Диг сделать + Диу ’ ДХ、 0 * = 1 / Диу,+ копать 2\, ДГ делать、 0,= 1 / ’ дичь + копать 2(.ДГ ДХ 。 ) (3.8).
- Индекс угловой деформации указывает, что угловая деформация происходит в плоскости, перпендикулярной определенной оси. И г. (Да-Ф) <И Или CO2 = __ / ’iu с _ ды * \ 2 \ ДХ делать} 63. Если скорость угловой деформации принимается согласно соотношению (3.8), то деформируемая поверхность должна быть повернута на несколько градусов для достижения истинного перемещения кромки parallelepiped. In в этом случае угловая скорость плоскости ABCB относительно оси 01 определяется следующим образом: Для угловой скорости плоскости относительно оси ОХ, оу, 02 получим следующее уравнение: со * = 1.
Таким образом, движение рассматриваемой плоскости выражается как сумма поступательных перемещений и вращений вокруг мгновенной оси, проходящей через полюс, деформирующее движение и Полюса. Чтобы установить применимость этого подхода ко всей частице, рассмотрим проекцию скорости в 2 точках, принадлежащих этой частице. Рассмотрим один из этих пунктов в пункт м, а это как дышло, и еще 1 в точке C(РНС.3.5) точки M и O находятся очень близко друг к другу в точке a / Away. In ряд Тейлора, скорость в точке O, vy, расширяет мгновенное значение проекции vm, ограничивая его линейным term.
Для проекции в точке O、 Из них= у + ^ Ах + ^ Ау + ^ Ар、 М ДХ ду ДГ Здесь они являются проекциями скоростей полюсов М. М. РТ 5 ^ 1 * дю < Частные производные-= и могут быть выражены в следующем виде И затем… Диг ДД, _1_ / Диг, \ Диу ДХ ’2 [ду дх я Диг \ 1_ / Диу __ МГП ДХ)2 \ ДХ делать АС+ Я Ау + Копать dh. АГ. Учитывая ранее введенные обозначения、 ХХ (1 = ummaxax + (8.Ай + 0й Ар)+(а> Яг о»р Ас).Для других составляющих скорости, + D * Lg)’ > \ =Дг+Дх+ 9 *ДУ)+(у*ДУ»VДх)> Где и….И, и, является проекцией скорости полюса частицы.
В соответствии с этим названием безвихревое движени жидкости называется потенциальным движением. Людмила Фирмаль
- Таким образом, мы убедились, что движение частиц жидкости можно представить как сумму поступательного движения, деформационного движения (линейного и углового деформирования) и вращательного движения вокруг мгновенной оси, проходящей через полюса. Поступательное движение характеризуется составляющей скорости Они\ \UI и Деформационное движение характеризуется линейной скоростью деформации dih _ diu _ dig dh’dodg
И угловая скорость деформации 0 * = 1 / dih! Диу. 2. 1. сделайте dh. 0х = 1 1 Диу• + копать 2(1 ДГ делать Копай, копай! 2 (, ДХ ДГ 5-788 65. Угловая скорость частиц жидкости относительно мгновенной оси, проходящей через полюса, характеризуется составляющей угловой скорости(компонентом). 1 / Диг Диу \ 2 1 ДУ ДГ]%= 1 1(Дич Ди、\ 2(^ ДГ ДХ) <sup class=»reg»>®</sup>г= » Диг Диу \ 2 (, ДХ ду 1 Вектор угловой скорости ω всегда перпендикулярен плоскости, в которой происходит вращение. Индекс
Смотрите также:
Возможно эти страницы вам будут полезны:

