Оглавление:
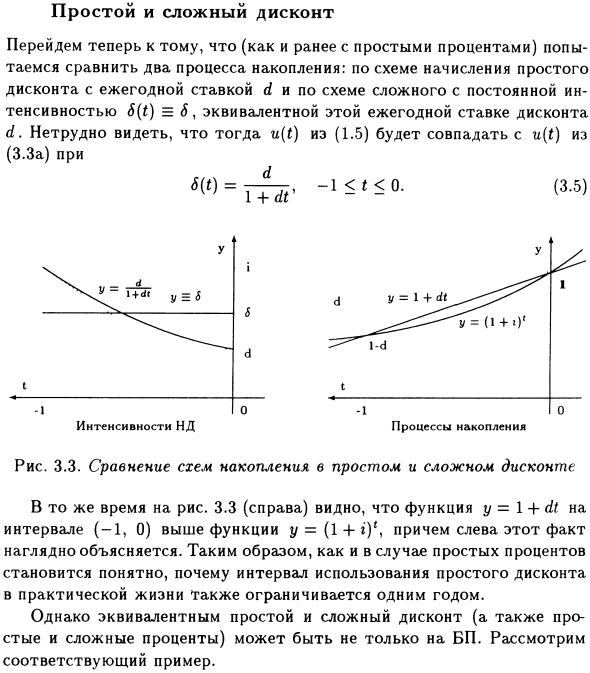



Простой и сложный дисконт
Простые и сложные скидки. Далее, давайте перейдем к тому факту, что (как и прежде) мы пытаемся сравнить два совокупных процесса с простым процентом:
- простую схему дисконтирования с годовой ставкой дисконтирования d, и это эквивалентно годовой ставке дисконтирования d
Следует сложной схеме с постоянной интенсивностью 8 (т) = 6. Людмила Фирмаль
Легко видеть, что u (t) в (1.5) на рисунке 1.5 соответствует u (t) в (3.3a). 3.3. Сравнение простых и сложных схем накопления скидок. В то же время ясно, что функция y = 1 + dt на рис. 3.3 (правый) интервал (-1, 0) выше, чем функция y = (1 + r) r.
Да и этот факт четко объяснен слева. Таким образом, становится понятно, почему интервал между использованием простых скидок в реальной жизни также ограничен одним годом, как в случае простого интереса.
- Однако сопоставимые простые и сложные скидки (а также простые и сложные процентные ставки) не ограничиваются БП. Рассмотрим соответствующий пример.
Пример 3.3 Коммерческие скидки При краткосрочной работе кредитор использует
так называемую годовую коммерческую ставку дисконтирования D, 0 0) Людмила Фирмаль
Рис. 3.4. Коммерческие скидки на самом деле сложны (Рисунок 3.4) с простыми скидками по разным ставкам (£) и предыдущим скидкам (/, i (то есть 1-d = v) и эквивалентные части (Z, 0))
Сравните скидки Итак, сначала получите уравнение 14-Dt = (14-i) \, затем достигните (3.6) и замените отрицательное t положительным t. Формат: d = 1- (1-Dt) 1 / *. 2. Из (3.6) используйте t ln (ld) = In (1-Dt) = -Dt- (Dt) 2 / 2- (Dt) 3 / 3- ••• ln (l-d) = -D-D2t / 2-D3t2 / 3.
Таким образом, ln (l-d) уменьшается как функция от t, ad-увеличивается • Наконец, еще один момент: на первый взгляд, рисунки 3.1 и 3.3 вызывают вопросы.
Является ли внешнее сходство СИС в этих ситуациях случайным или соответствующая функция 6 (t) действительно сдвинута? Во-вторых, точнее, если функции (3.1) и (3.5) обозначены через r- <5, (1 + 0 = -1 0 или int, рассчитывается для t <0),
но формула ( 3.9) предлагает себя по национальным причинам: 200 или 100 при тех же условиях, которые не должны влиять на интенсивность, поэтому мы говорим о скорости изменения капитала по отношению к этой единице Он должен иметь
Смотрите также:
| Простые и сложные проценты. | Накопление и приведение. |
| Простой дисконт. | Обычный процесс накопления. |

