Статически неопределимые задачи при растяжении и сжатии

Статически неопределимые задачи при растяжении и сжатии

Проблемы, которые не могут быть определены статически при растяжении и сжатии Продольная сила, действующая на стержень системы, не может быть определена только из статического уравнения, но необходимо учитывать деформацию системы. Такая система называется статически неопределенной.

• Простой пример такой системы показан на рисунке. 18.Нагрузка P вызывает натяжение на сопланарных стержнях OB, OS и 00.To определите 3 неизвестных напряжения стержня, статики дают 2 уравнения равновесия; чтобы составить 3-е уравнение, необходимо учесть деформацию системы.

Для простоты, мы предположим, что сим-рисовые системы. 18.Метрика относительно вертикальной На оси OS, вертикальный стальной стержень c. модуль упругости площади поперечного сечения R g и материала Ec, а наклонный стержень-медь с площадью/ 7 м и модулем упругости Ey.

Длина вертикального стержня равна/、 я наклонный стержень-представляют собой силу наклонного стержня с натяжением вертикального стержня и X, в этом случае из-за симметрии мы видим, что существует 2 неизвестных, а статика дает только 1 уравнение равновесия. 。 А4-2ycosa = п. (а）

Для того чтобы вывести 2-е уравнение, необходимое для определения неизвестных величин X и Y, необходимо учитывать контур деформационной системы, который обозначен пунктирной линией на рисунке. Под действием нагрузки P D / происходит полное выдвижение вертикального стержня. Далее, расширение наклонного стержня с / ф получается из Офот треугольника.

Наклонный стержень будет очень длинным, и вся нагрузка будет распознаваться центральным стержнем. Людмила Фирмаль

Предполагая, что эти расширения очень малы, можно заменить дугу окружности перпендикулярной линией в центре D и принять угол Oi равным исходному углу a. и тогда… А /,> = а / коза. Относительное удлинение и напряжение вертикальных и наклонных стержней соответственно г _ д /. N ФК Д / А / соѕ * а. £M_A / COS в * а ■/«°с-I•и ~~ я «〜» я Далее, прикладывая напряжение к площади поперечного сечения, получают усилие стержня. А/, г = oKFK= -?Е » âillcosta,(б） Г-х Кос * г Я…

Откуда? F uCd FCEC * При вставке в формулу(а)、 *- город г(10） 。 1 + 2 cos * рктк. Видно, что Сила Х зависит не только от угла наклона а, но и от площади поперечного сечения и механических свойств материала стержня. Из Формулы (10), если все стержни имеют одинаковое поперечное сечение и одинаковый модуль упругости В Ф. ’- ЛГ = 1- * 2cos * КТ- Когда сила приближается к нулю, cos a приближается к 1, а сила вертикального стержня приближается к-R. Когда a приближается к 90 градусам、

Другим примером статически неопределенной системы является призматическая балка с ребром, вложенным под действием силы. Применяется для промежуточного П \ * Вдоль оси луча. Грузовые П、 1 ′ раздел TP(Рисунок 19) и ток Ты хочешь поделиться со мной? второй? Поэтому * 4-1Тим■р = х + * л. 。 (С） О 1.; Я… / ■;

Чтобы создать 2-е уравнение для определения силы/?И деформация луча Я19 должна быть рассмотрена. Груз Р и сила/? \ p ’ укорачивает нижнюю часть балки. 1 / х силой? Расширение верхней секции. Много. Рисунок 19. 1. укорочение одного участка должно быть равно половине. Еще одно расширение.

Затем, используя уравнение Неэлемент(1), получаем ПХ ПБ Следовательно、 ^ 0 едите\ го;».Т•»> То есть реакции H и R обратно пропорциональны расстоянию приложенной точки от поперечного сечения нагрузки mn. Используя формулы © и (e), можно легко рассчитать величину этих реакций и напряжение стержней.

• Задачи. Диаметр стального цилиндра и наружный диаметр медной трубки сжаты между пластинами пресса(рис.20). P 40 t,^ = 10 см и£> = » для 20 см определяют напряжения стали и меди, а также относительное укорочение. • Решение. Опять же, уравнений статики недостаточно, поэтому для получения нагрузки, которую воспринимает каждый материал, необходимо учитывать деформацию цилиндра и трубы.

Относительное укорочение стали и меди должно быть одинаковым. Таким образом, напряжения в материале будут иметь такое же отношение, как и их модуль упругости (см. уравнение (4)), то есть напряжение сжатия в стали yy будет напряжение сжатия меди. Далее определяют величину напряжения меди ом из уравнения электростатического давления. Ла * 20. Я / ОА. пожалуйста, посетите для получения дополнительной информации. — xx° » + 4-Нет* -^) am. 96.6.10′*. К 0M = 10O6 кг/ см2; os » = 193 кг / см2 И относительное сокращение

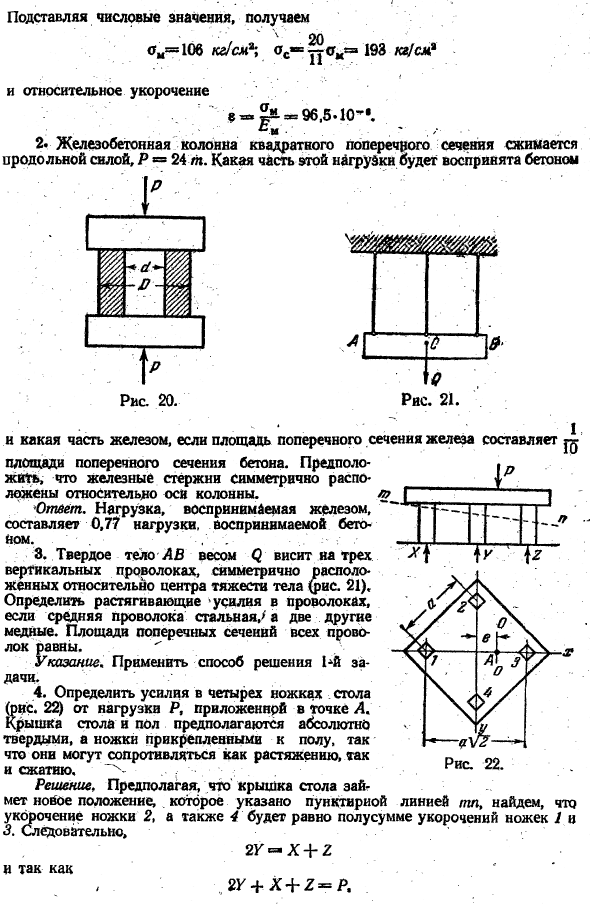
2.Железобетонные колонны квадратного сечения сжимаются продольной силой Р = 24 тонны. Какая часть этой нагрузки впитывается в бетон ’ * ■ • ’1 Если площадь поперечного сечения утюга^, то какая часть утюг Площадь поперечного сечения бетона. Возможно. Железные стержни симметрично{ Позиционируется относительно оси колонны. L G 1 Отправление.

Нагрузка, которую чувствует железо, г〜 » г-г〜^ В частности, нагрузка составляет 0,77. —. •:*•; .• 3. Твердое тело A A B веса Q подвешено на 3 вертикальных проводах, расположенных симметрично относительно центра тяжести тела{фиг. Двадцать один） Если Центральный стальной провод / a равен 2, Определите натяжение провода.

Другая медь. Площадь поперечного сечения всех проводов одинакова. Показания Pj применяют методы для решения проблемы. 4.По нагрузке Р, приложенной к точке А, определите усилие на 4 ножках стола (рис.22). Верхняя часть и пол таблицы совершенно крепки и ноги прикреплены к полу, поэтому они могут выдержать и протягивать и обжатие.

Решение, предполагая, что крышка стола занимает положение, обозначенное пунктирной линией tp, можно видеть, что укорочение ножек 2 и 4 равно половине суммы укорочений ножек 1 и ножек. 3.В результате、 2Г Х + 2 И с тех пор 。 2У + х + р = р Дополнительное уравнение для определения X и 1 получается путем взятия моментов всех сил, проходящих через точку A параллельно y относительно горизонтальной оси O_O. (Є） Х (±ай2 + е} +±Ре = Р (±ай2-эй (Да получить из (e)и (0 О） г(я + т） Икс год= в случае e> a-X мы знаем, что он отрицателен.

При решении этой задачи следует отметить, что если точка приложения нагрузки р не находится на диагонали стола, то эта нагрузка заменяется на 2 веса Людмила Фирмаль

Это указывает на то, что растяжение происходит на ноге 1. a. определите усилие ноги над указанной таблицей, если точка с координатами имеет нагрузку Но… Но… г ~ ~ Б » которые эквивалентны нагрузке Р и статически приложены к точкам, которые находятся на 2 diagonals. As упомянуто выше, от каждой из этих нагрузок обнаруживается сила, возникающая в ноге.

Суммируя работу 2 составляющих Весов, можно найти усилия ног относительно любого положения груза R 6.Прямоугольная рама с диагональю подвергается воздействию сжимающей силы Р(рис. 23).Если все они выполнены из одного и того же материала, то определяют усилие стержня, площадь поперечного сечения вертикального стержня равна Р, а площадь остального стержня равна/ ч.

Решение. Пусть X — сила сжатия каждой фигуры. 23 вертикаль, Y — сила сжатия каждой диагонали Натяжение каждого турника. Тогда из 1 равновесного состояния шарнира： П-Х. 1 = » ГП А = Е (П-Х) для сі£а. U- (2） 3-я формула получается из условия, что после деформации каркас остается прямоугольным из-за симметрии. Поэтому’, <°* +Л * >(! «А)=Л1(1-а» (’+ст;)’

Из этого уравнения, если вы игнорируете небольшое количество более высокого порядка、 <о * + л *)ЕР г _ ах, ЕП, ’ (Си> Год= Другие усилия стержня теперь можно легко определить из уравнения (£). 7. установите a> = A, P * 3 b / 7 и P = 20m для решения предыдущей задачи. 8.Напряжение на стальных болтах и медных трубах (рис. 24） При повороте гайки, если длина болта составляет 1 = 75 см, шаг резания Болта k = 0,3 см, площадь поперечного сечения Болта составляет Pc = 6 см2, а трубки Rm = 12 см2?Тебе решать. Х как неизвестное натяжение Болта Сила сжатия в трубке.

Величина X определяется из условия, что укорочение трубы и растяжение сложного Болта равны перемещению гайки вдоль оси Bolt. In в этом случае предполагается, что длина трубы равна длине Болта、 Запад. / Запад. Откуда? 6286 кг. 41 (,+ Вт 4-75 ^ 1 + Рис.24. 0.3-2.10 ′* 6 И затем Растягивающее напряжение Болта равно bs «1048кг / см *.Сжимаемость — гг» 524 кг / см ** Г. М.

Напряжение в трубке составляет около 0.Если напряжение P = 2 t приложено к обоим концам Болта, как изменяется напряжение, рассчитанное в предыдущей задаче Решение. Увеличьте растягивающее усилие болта до X и уменьшите сжимающее усилие трубки до K. затем выйдите из равновесия P’x + Y = * P. (I） шмат / л 2-я формула может быть записана на основании того, что относительное удлинение болта и трубки под действием силы Р должно быть равным. Ф Рис.26.

Вы из уравнений e (1) и 0) можно легко вычислить силы X и Y, а также соответствующие напряжения. П 10.Луч призмы, которая закреплена с обоих концов, нагружен силами P и PB в направлении оси в 2 промежуточных секций(рис. 25). Op-R и P Рисунок 25. ’Поделитесь своими реакциями Примечание * формула(<!С помощью функции () можно рассчитать индивидуальные реакции, вызванные каждой силой, на стр. 28 и суммировать эти реакции. a= 0,3/, b = 0,31 и P, = «2P», определяет реакцию в случае 400 кг.

Ответ. Р = 240 кг. Р, = 360 кг. 11.Определите мощность стержня в системе, которая показана на рисунке. 26, где ОА-ось симметрии. * ’г： Ответ. Натяжение штока ом равно силе сжатия L стержня OS — J sin a. мощность горизонтального стержня OA Обнулить. …. Вт.«• 12.Решаем задачу 10, предполагая, что площадь поперечного сечения нижней части балки длины С в 2 раза превышает площадь поперечного сечения верхней части балки длины а и В… — Это ответ. ». • ’. ‘- 2Н, о + 2Р.(/- £ ), Р, (26 + е)4-П Е — .И-с * КТ 21-С.•**

Смотрите также:

Предмет сопротивление материалов: сопромат

Начальные и температурные напряжения	Допускаемое напряжение
Растяжение кругового кольца	Напряжения и деформации при действии собственного веса