Напряжения и деформации при действии собственного веса

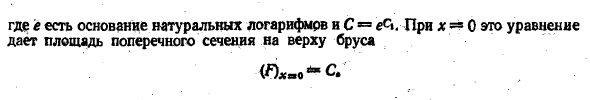
Напряжения и деформации при действии собственного веса

Напряжения и деформации, обусловленные действием собственного веса При рассмотрении удлинения стержня согласно рисунку 1 учитывалась только нагрузка, приложенная к концу вала. Если длина стержня длинная, то из-за собственного веса может возникнуть значительное дополнительное напряжение, которое необходимо учитывать account. In в этом случае максимальное напряжение находится поперек поперечного сечения в конце.

• Если вес единицы объема древесины выражается через y, то его общий вес будет равен y / 7, а максимальное напряжение будет определяться из уравнения. (6） Я посмотрю, что можно сделать. один. 2-й член в правой части уравнения (6) представляет напряжение, вызванное весом балки. На расстоянии x от нижнего конца (Рис. 1) масса сечения балки под сечением mn равна y / 7*, напряжение этого сечения определяется по формуле Подставляя в формулу (6) вместо допустимого напряжения[а], получаем формулу для расчета требуемой площади поперечного сечения. (8）

Интересно, что по мере увеличения длины I веса балок становятся все больше и больше. Людмила Фирмаль

Знаменатель в правой части уравнения (8) уменьшается, а требуемая площадь поперечного сечения V7 увеличивается. y / = *(a 1, то есть правая часть уравнения (8) бесконечна, если напряжение от балки только собственного веса равно допустимому voltage. In в такой ситуации невозможно спроектировать призменную балку, и приходится прибегать к балке переменного сечения.

Для расчета суммарного удлинения призматической балки, которая растягивается под действием силы, действующей на ее конец, силы Р и собственного веса, сначала рассмотрим удлинение элемента длиной c£ £ x, который отрезан от балки на 2 смежных поперечных сечения(см. Рис.1).Растягивающее напряжение является постоянным на очень короткой длине, xx, и можно предположить, что оно определяется из уравнения (7).

Затем расширение элемента Ds / x А<1х Р4 — БВГ、• — Тг — = ’ — ТТ’ Полное растяжение луча получается суммированием растяжения всех элементов. И затем… < 9> Если мы сравним это с уравнением(1), то увидим, что полное удлинение, вызванное собственным весом балки, равно удлинению, вызванному нагрузкой, равной половине ее веса и приложенной последней.

• Задачи 1.Определить площадь поперечного сечения вертикальной квадратной колонны стальной балки (Рис.1) длиной 200 г, с допустимым напряжением 1 <t] = 700 кг / см*, массой 1 куб. см и нагрузкой 30 т на нижний конец балки. Определить общее удлинение балок, равное 7,8 г. Решение, площадь поперечного сечения уравнения(8) 30000 ′ 55.15 см *.

Полное удлинение от 700-0. 0078-20 000 формула(9) D / = TSC *(544 + y-156)= 6.22 см 2.Если длина балки равна I диаметр основания, вес единицы объема материала-г, то под действием собственного веса определить удлинение конического пучка(рис. 14).

Решение. Вес балки равен n пс1я 1 ^ ТТ ’ Для участка на расстоянии х от нижней кромки балки растягивающее усилие, равное весу нижней части балки, составляет (іх я <£• ’ * л \ — • * г. «■»*«5. Предполагая, что растягивающее напряжение равномерно распределено по поперечному сечению) и рассматривая элемент длины ah в виде призмы, мы можем видеть удлинение этого элемента МММ. D слева. Ф Полная протяженность луча я… • д. /» Удлинение составляет 3 минуты 1 от удлинения призменного пучка той же длины(см. уравнение (9)).

8.Вертикальный призматический вал вала насоса перемещается вверх и вниз с помощью коленчатого вала (рис.15).Определить площадь предполагая, что материал стальной и допустимое напряжение составляет (o] 500 кг / см1 Если сопротивление движению поршня вниз составляет 100 кг, а Движению вверх-1000 кг, то поперечное сечение штока.

Длина штока*составляет 100 м. Если ход поршня равен 20 см, то определяют требуемую длину радиуса изгиба g. требуемую площадь поперечного сечения штока определяют по формуле (8) путем подстановки 1000 кг… Рис.15. 1000. 2.37 см *. Из-за сопротивления поршня, разница между полным расширением штока при перемещении штока вверх и вниз、(1000 + 100). 10 000 ^ л. Л <〜 — л ’»-5P5G53T-2.32 ″ ч- Радиус колена должен быть 20 + 2,32 11.16 ом. Г — 5— 4.Стальной провод и алюминиевый провод повешены вертикально.

Форма луча, удовлетворяющая этому условию, называется формой эквивалентного сопротивления. Людмила Фирмаль

Для стальной проволоки•= * * для 20 000 кг / см *и y = 7,8 г / см9, а для алюминиевой проволоки » ^ » ZZOO кг, для каждой проволоки, определяют длину, при которой напряжение от собственного веса равно пределу прочности на растяжение. ！см и y = 2,5 г / см *.Ответ. Для стали= = 25,640 м, а для алюминия= = 13,200 м. Все размеры балки p i .При увеличении относительно 1 (рисунок I), в каком отношении максимальное напряжение, создаваемое призменным пучком, увеличивается от его собственного веса?

Ответ. Напряжение возрастает по отношению к n 11 6.Колонна, состоящая из 2 квадратных секций колонны равной длины (рис.16), сжимается от середины верхней кромки с силой сжатия Р = 240. *) Это предположение справедливо, когда угол конуса мал. Если высота колонны составляет * 36 м, то объемный вес составляет 1,6 т / м, а максимальное напряжение сжатия для каждой секции составляет 10 кг!

См. Сравните объем этой колонки с объемом простой призмы, сконструированной в тех же условиях. Решение. Площадь поперечного сечения верхней части колонки ns в формуле (8)равна «: 240000 32 880 ′ см * = 3,288 м *. 10-0. 001 ^ 1850 Для нижнего 10-32 880ІО-О.総量бб-і і общий объем кладки равна 46050 см * = 4,505 м *. В =(3.288 + 4.505)18 » 140.274 м *. P для призматических колонн. 240000. Эй, Эш. Рис.16. 52,170 см * * 5.217 м * * ■ = 10-0. 0015-360с 5.217-36 = 187.812 л *.

7.Решим предыдущую задачу, предположив, что колонна состоит из 3 призматических секций одинаковой длины. 。 Ответ. П «2.927 ма, ПГ» 3.570 м \ ТР4. 354 м \ в = » 130.20 *•. 8.Определите форму луча на фиг. Решение. Учитывая заштрихованный стержневой элемент на рисунке, можно видеть, что сжимающая сила поперечного сечения t, n больше сжимающей силы поперечного сечения на величину веса элемента.

Однако, поскольку напряжение в обоих сечениях одинаково у обеих женщин[а], разница в площади поперечного сечения Р должна быть такой, чтобы компенсировать разницу в сжимающих силах. Поэтому■,「* г [о | = УР ых、 （* Где правая сторона-уравнение, представляющее вес элемента. Разделим это уравнение на/ ^ a], а пронет-найдем Запеченные, мы ГТ. Куо ) ТФ] 1 Откуда. + С| Хм… м. 1pG. т. * Р = CeIv1. (Си）

Где e-основание натурального логарифма, А C * = e&. для x ^ 0 это уравнение дает площадь поперечного сечения верхней части балки < Lftho ** С * Р п Но площадь поперечного сечения верхней части одинакова. Следовательно, С-и Формула (b)получается в виде: П. С.〜 (с） м. Площадь поперечного сечения нижней балки получается путем подстановки Формулы © х=/. П. С.- 9.При условиях, принятых в задании 6, найти объем кладки из равнопрочных балок.

Решение. Используя уравнение ((3)), найдите разницу между площадью поперечного сечения верхней и нижней части колонки * * * * * * * * * * * Т И —21 21 (е [о) _l, за. \ °Г г р г Значение этой разности, умноженное на допустимое напряжение.

Смотрите также:

Предмет сопротивление материалов: сопромат

Статически неопределимые задачи при растяжении и сжатии	Диаграмма растяжения
Начальные и температурные напряжения	Допускаемое напряжение