Оглавление:







Допускаемое напряжение
Допустимое напряжение Растяжимая диаграмма обеспечивает неоценимую информацию о механических свойствах материала. Зная пропорциональный предел, предел текучести и предел прочности на растяжение, можно задать значение напряжения для каждой конкретной технической задачи, которое можно рассматривать как безопасное напряжение.
- Это напряжение обычно называют допустимым напряжением. При выборе величины допустимого напряжения стали, напряжения ниже пропорционального предела, этот материал можно считать полностью упругим, но после такой разгрузки необходимо учитывать, что стержень обычно остается частью деформации, то есть остаточной деформации.
Обычно он принимает допустимое напряжение, которое немного ниже пропорционального limit. In для экспериментального определения этого предела требуется чувствительный измерительный прибор (экстензометр), так как величина этого предела зависит от точности измерения. measurement.
To устраняя эту трудность, предел текучести или предел прочности при растяжении материала обычно берется за основу для определения величины допустимого напряжения. (o), am и допустимое напряжение, предел текучести и предел прочности на растяжение материала показаны соответственно, а величина допустимого напряжения определяется из следующего уравнения: [СТ] = ^ или [O)=?в..(5)
Где 6 и kx-постоянные величины, называемые коэффициентами безопасности, определяющими величину допустимого напряжения. Для строительной стали логично взять предел текучести за основу для расчета допустимого напряжения. Это неудивительно, ведь на этом пределе происходит большая остаточная деформация, что недопустимо в технике structures. In в этом случае коэффициент запаса прочности/ g = 2 дает достаточное значение для допустимого напряжения, если конструкция подвержена только постоянному или статическому воздействию loads.
Это неудивительно, ведь на этом пределе происходит большая остаточная деформация, что недопустимо в технике structures. Людмила Фирмаль
В случае внезапных или переменных нагрузок, которые часто наблюдаются на деталях машин, необходимо принимать больший запас прочности. Для хрупких материалов, таких как чугун, бетон, различные типы камня и такие материалы, как дерево, предел прочности обычно используется в качестве основы для определения допустимого напряжения.
Этот предел может быть установлен при измерении удлинения с помощью очень чувствительного измерителя перемещения. Грюнельсен, см. Вег. Эй, физик, ГЭС. И 1906 г. Величина запаса прочности зависит от точности определения внешней силы, действующей на конструкцию, точности, с которой можно рассчитать напряжение на части конструкции, а также от однородности используемого материала.
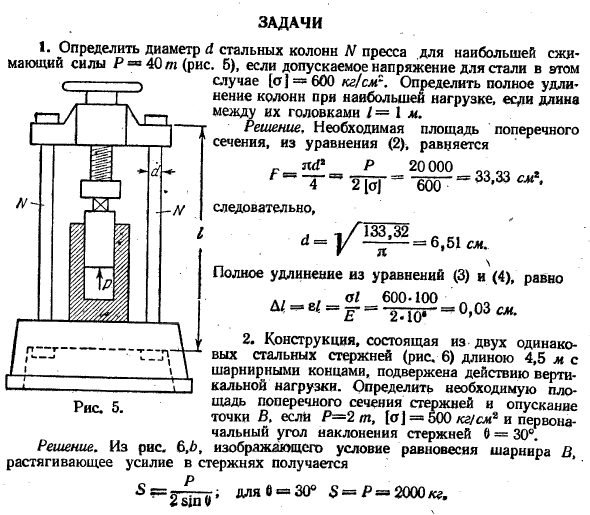
Эта важная проблема допустимого напряжения обсуждается более подробно ниже (см. Часть I). Вот несколько простых примеров определения твердого размера поперечного сечения стержня, предполагая, что задано допустимое напряжение. И И… ■И Это… Д. / 2-10. * Рисунок 5. 1.Определить диаметр (максимальное усилие сжатия Р = 40 т) (рис. Допустимое напряжение стали Случай 1С = 600 кг / / если длина между головками ПЛ1 \ i / = 1 м, определить общее удлинение колонны при максимальной нагрузке. д*) — * решение.
Требуемая площадь поперечного сечения Сечение из уравнения (2)равно тир 20000 р Г » — «* — щ — — — щ — » 33> 33• 2.Конструкция, состоящая из 4,5 м длиной, 2 одинаковых стальных стержней с шарнирными концами (рис.6) подвергается вертикальной нагрузке. Определите требуемую площадь поперечного сечения стержня и точку опускания B. Для Р-2 т, Ат / о] = 500 кг / см2, начальный угол наклона стержня равен 0 = 30°.Равновесное состояние сустава B、
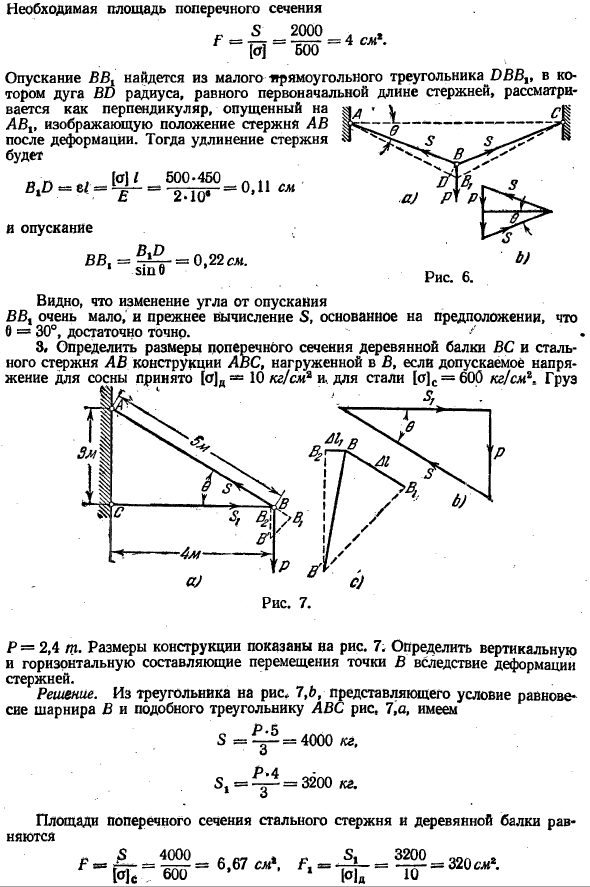
Решение.6b из рисунка получается натяжение стержня «, яв » 30° Следовательно、 0,03 см. 6.51 см 2000 километров. Общее удлинение по формулам (3) и (4) составляет、 600-100. Требуемая площадь поперечного сечения −5 и 2000. 。 ^ =Т«= «= 4см» [а] 600 Каплю ВВХ можно найти из небольшого прямоугольного треугольника))) VV. In VV, дугой радиуса, равного начальной длине стержня (VG), считается провисание при AVX, что указывает на положение стержня AB после деформации.
Мы видим, что угловое изменение из-за снижения BB1 очень мало, и предыдущий расчет 0 = * 30°основан на предположении, что 5 является очень точным. Людмила Фирмаль
После этого выдвижение штанги И капля −0.11 см 0,22 см. 500-460. 2-10. 3, Если допустимое напряжение сосны приемлемо, определить размеры поперечного сечения деревянных балок самолета и конструкции Лан стальными стержнями АВ, нагруженными на V[cr] d » 10 кг/см2 И. Для стали[a] c = 60 кг / см2, груз Один. Р = 2,4 т.
Размеры конструкции показаны на рисунке. 7.Определите вертикальную и горизонтальную составляющие смещения точек B вследствие деформации стержня. Решение. Равновесное состояние соединения B показано на рисунке* 7.6, как и в треугольнике LAN на рисунке 7 a、 5 = ^ 5 = 4000 кг. Р. А. 51 = = £ _ ^ = 32oo кг. Площадь поперечного сечения стальных прутков и деревянных балок равна / $ 4 <* х> *. Инжир. Шесть Тюнинг%о ВВХ = БИПО. 3200. •5 / 4000-500•• _ 1С. £c_ ’a-10, −6.67″ ° — 15sl ’ .. 5,/, 3200-400… d.、»»= 10 -^ 20 =°’04
Чтобы определить смещение шарнира Б из-за деформации, мы описываем дуги с центрами а и с(рис. 7, а). радиус, соответственно, равен длине удлиненного стержня и сжатой балки. Петля B пересекается в новом положении B’.Рисунок 7c, где 23B-удлинение стального стержня, а Вг-укорочение деревянной балки. Пунктирная вертикальная линия заменяет вышеприведенную дугу.
Таким образом, VK-это движение шарнира B. компоненты этого движения можно легко получить из чертежа. 4.In предыдущая задача, определить угол наклона стержня АВ так, чтобы его вес был минимальным. • ’ Решение. Если 0 обозначает угол между стержнем и горизонтальной балкой, а 2-длину балки, то длина стержня равна/=/, / co5 b, а натяжение стержня равно требуемой площади поперечного сечения Р гшш РК], 5ИП б. объем стержня CR. 21.П. С.
Видно, что объем и вес стержня наименьшие в грехе 20-1. «О = 45°. ‘• 5.Квадратная рама ABCD (рис. 8, А), состоящая из 5 стальных стержней, поперечное сечение которых составляет b см*, подвергается действию 2 сил P => 4 t в диагональном направлении. Определить величину изменения углов а и с вследствие деформации frame. As на рисунке 8 показано, насколько изменяется один и тот же угол при приложении силы.
Решение. Если это показано на рисунке 8а, то диагональ принимает всю нагрузку R. Если предположить, что шарнир D не перемещается и направление диагонали не изменяется, то можно увидеть, что перемещение шарнира B в направлении диагонали равно расширению диагонали a / * =»PifEF. Определение нового положения c соединения C обозначено пунктирной линией на рисунке.
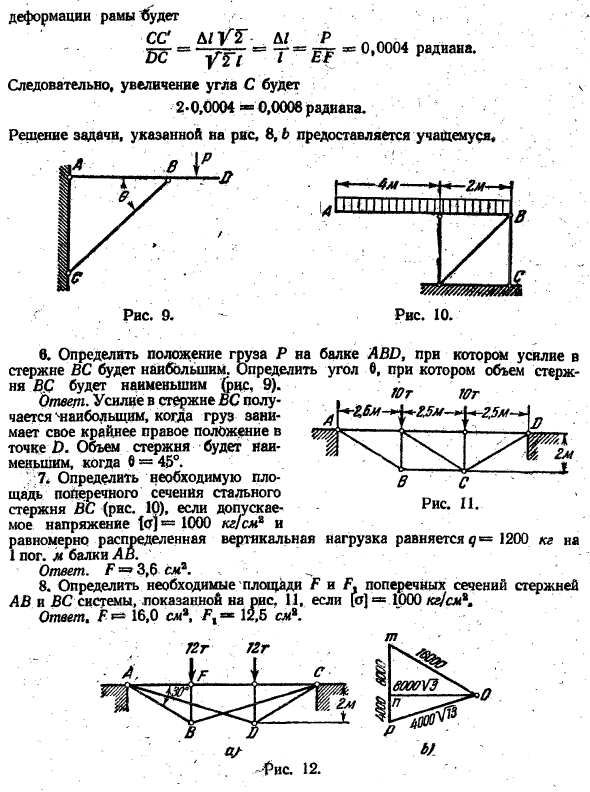
Из небольшого прямоугольника CCXC, CC = A / / Y? Вы можете видеть, что это хороший пример. Далее, угол поворота стержня DC Деформация рамы Судет*/.. 4,.. СС д / ут-.D / I LPP ^ W = » rt7 = 7 = ^ = 0.0004 Радиана. Таким образом, увеличение угла C равно 2 * 0,0004 * » 0,0008 рад. 1, Решение задачи, показанной на рисунке 8B, предоставляется студентам. 0
Определите положение нагрузки P балки ABD, при котором сила тяги BC будет максимальной. Определите угол, определяющий, где объем стержня BÇ минимизирован(Рисунок 9). The answer. It видно, что сила тяги летательного аппарата максимальна, когда нагрузка находится в наиболее правильном положении в точке D. объем тяги минимален, когда Ô= 45°. ’;
7.Определите необходимую площадь поперечного сечения стали Стержень самолета (рис. 10), если допустимое напряжение составляет 1°C) Ооооог кг / см * и perpendicular ^ perpendicular перпендикулярная скорость. %• 8 * определите необходимую площадь Р и А поперечного сечения стержней AB и BC системы, показанной на рисунке. 11 [a \ = 1000 кг / см * Ответ. 16.0 ХЛ *. 12,6 см. *
Мое напряжение составляет 1 . 11 и полное удлинение стержня, если его материалом является конструкционная сталь n [a] » 1000 кг / см. Ответ. P = 16 см2, A / = 0,16 см. 11.Предположим, что нагрузка приложена только к 1 узлу верхнего ремня на расстоянии 2,5 м от опоры, после чего решается задача 8. Ответ. Р * = 10.67 см2, РХ-8.33 см2. 12.Квадратная стальная рама крепится, как показано на рисунке. 13.Найти полное удлинение каждого стержня, если площадь поперечного сечения всех стержней одинакова и составляет 5 см2. Ответ. Удлинение всех стержней, кроме AB, равно нулю. Для стержней AB A / = 0,3 см. 4000 V13 * 1000 16000. 1000. 16 см2 П — = 14,4 см2.
Смотрите также:
Предмет сопротивление материалов: сопромат
| Напряжения и деформации при действии собственного веса | Закон Гука |
| Статически неопределимые задачи при растяжении и сжатии | Диаграмма растяжения |

