Закон Гука

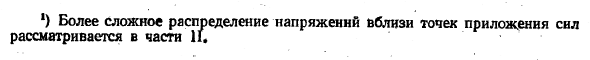
Закон Гука

Закон Гука. Прямой эксперимент по удлинению стержня призмы (Рис. 1) показывает, что удлинение стержня в некоторой степени/ / y во многих строительных материалах// // // // // было установлено, что прочность на растяжение W /пропорциональна. Это очень просто \ Линейная зависимость силы и удлинения、 /То, что она называет первым, было сформулировано- 7-е -.Г, британский ученый, Роберт Хук 2) 1678, носящий его имя.

• Использование вывесок： y _ п1пР—силы, чтобы растянуть стержень、 I * / — длина стержня、 I m P-площадь поперечного сечения стержня^ V’D / — полное выдвижение штанги、 a * E-постоянная упругости материала、 Рисунок 1.Модуль растяжения Экспериментальный закон Гука можно выразить Следующее уравнение： Л / Н9> __ ФВ. *

Удлинение стержня пропорционально растягивающей силе и длине стержня и обратно пропорционально площади поперечного сечения и упругости modulus. In продукция растяжимого испытания, все меры предосторожности обычно приняты для обеспечения что растяжимое применение Центрально x)в этом исследовании небольшие изменения температуры ignored. It обычно сопровождается упругой деформацией и соответствует теплообмену со средой (см. Часть I). а) Роберт Гук, De Potentia restitutiva, Лондон, 1678 г.

Сила. Рисунок на этом рисунке показано, как закрепить конец круглого испытательного образца с помощью растяжения Tester. In таким образом, предотвращается изгиб стержня. Исключив из рассмотрения ту часть стержня, которая близка к точке силового Воздействия1), можно сделать вывод, что при растяжении все продольные волокна призматического стержня имеют одинаковое удлинение и удлинение, а поперечное сечение стержня изначально является плоским и перпендикулярным оси стержня, и остается неизменным.

При определении величины внутренней силы представьте себе стержень, разрезанный на 2 части поперечным сечением TP и рассмотрите баланс нижней части стержня(рис.1.6). На нижнем конце этой части приложено напряжение R, и сила, действующая на верхнюю кромку, указывает на то, что верхние частицы деформированного стержня действуют на нижние частицы. Эти силы распределяются непрерывно по поперечному сечению.

Близким примером непрерывного распределения сил на таких поверхностях является гидростатическое давление или давление пара. Людмила Фирмаль

Для такой непрерывно распределенной силы сила силы, то есть сила на единицу площади, очень велика. important. In в этом случае при осевом растяжении, при котором все волокна имеют одинаковое удлинение, распределение сил по сечению mn будет равномерным.

Результат действия этих сил passes. It является центром тяжести поперечного сечения и действует вдоль оси стержня. Рассмотрим, что сумма этих сил из состояния равновесия (рис.1.6) должна быть равна Р, а через а обозначим силу на единицу площади. ЧР = Т•(2） Эта сила на единицу площади называется растягивающим напряжением или просто stress. In в будущем напряжение измеряется в килограммах на 1 квадрат, так как сила измеряется в килограммах, а площадь измеряется в квадратных сантиметрах.

Удлинение стержня на единицу длины определяется по формуле д. / ) В Части II учитываются более сложные распределения напряжений вблизи точки силового воздействия. Модуль упругости равен напряжению, деленному на относительное удлинение, и может быть легко рассчитан, если напряжение и соответствующее удлинение определяются из испытания на растяжение.

Удлинение е-это абстрактная величина, представляющая собой отношение 2 длин (см. уравнение (3)). Таким образом, из Формулы (4) можно сделать вывод, что модуль упругости измеряется в той же единице, что и напряжение а, то есть в килограммах на 1 квадрат. Среднее значение модуля E для некоторых материалов см. В таблице I1 в колонке 2.

И это называется растяжка или растяжение. Используя уравнения (1)«(2) и(3), можно записать закон крючка в виде: T Таблица 1 Механические свойства материалов Материал е кг / см ’ 1 предел текучести кг / см * предел прочности в кг / см2 Углеродистая сталь 0.15-0.25° / 0 углеродистая никелевая сталь 3-3. 5°/ 0 никель вместе с дюралюминием холоднокатаная медь медь стекло Сосновое волокно. 。 。

Сжатие бетона 2. 1. 10×2. 0. 10×0. 70. 10×1. 1. 10×0. 70. 10×0, Х0×0. 28. 10×2. 1. 10 «-2.8. 10×2. 8. 10 е-3.5. 10×2. 4. 10 е-3.1.10. е. 3.9.10 ^ е — 4.6.10 е 5.4.10 е — е 7.0.10 3.8» 10 ″ — ^ 4.6″ 10е 2.0.10 е — 2.8.10 е 2.5-10 * 5.6-10_ -!, 4.10 е.2.10 е Формула(1) — (4) также может быть применена в случае сжатия стержней призмы. Далее, D / обозначает полное продольное укорочение, e-относительное укорочение, а-сжимающее stress. In большинств строительные материалы, модуль упругости во время обжатия это же как модуль во время tension.

In расчет, напряжение растяжения и деформация растяжения считаются положительными, а напряжение сжатия и деформация растяжения считаются отрицательными. * ) Детали механических свойств материала описаны в части 11.

Далее, D / обозначает полное продольное укорочение, e-относительное укорочение, а-сжимающее stress. In большинств строительные материалы, модуль упругости во время обжатия это же как модуль во время tension. In расчет, напряжение растяжения и деформация растяжения считаются положительными, а напряжение сжатия и деформация растяжения считаются отрицательными. * ) Детали механических свойств материала описаны в части 11.

• Задача 1. Если растягивающее напряжение составляет 1000 кг / см*, определяют общее удлинение стального стержня длиной 60 см. — Ответ. Л / = * 0.03 см

2.Если относительное удлинение составляет 0,7 «10»#, то определяют усилие на растяжение цилиндрических стальных стержней диаметром 1 см.

Решение, растягивающее напряжение стержня из уравнения(4) >. o = » £ » = 1400 кг / см2 Напряжение из уравнения(2) П-о / «= 1400-4 — = 1100 кг. 4.

3.Каково отношение модуля упругости материала 2 стержней одинакового размера, если оно относительно под действием одинакового натяжения Удлинение 4 стержней 20 составляет отношение 1: е- 1 из штаног сталь, другое 1 медь, растяжимое усилие 600 kg! см.* Да. Один.

Модуль упругости обратно пропорционален удлинению Людмила Фирмаль

Решение. . Для стали = 0,00030,1 ^ усл Для меди ■я • * є = 0,00054. Р. П. С. I ^ USM 4.Под действием растягивающей силы Р длина квадратного бруска 60 см удлиняется на 0,06 см. Ответ. Р-12000 кг. а. проволока с усилием растяжения Р-400 кг, на длину которой воздействуют 30 м, тянется на 2,5 см.

Если поперечное сечение проволоки составляет 0,3 см2, найдите модуль упругости материала. 13-USM Т. Ответ. Е = 2-10 кг / см *. 6.10 см2»/ / * * * ** Функционирование мощности φ-4m и P = * bn fis. 3). Решение. Верхнее и более низкое напряжение штанги<2, и среднее напряжение<2-п. После этого, полная удлиненность будет: TE. 7.Предполагая, что материал дюралюминиевый и меньше 2-4 / Р, решаем задачу 6.

Смотрите также:

Предмет сопротивление материалов: сопромат

Упругость	Диаграмма растяжения
Закон Гука	Допускаемое напряжение