Оглавление:






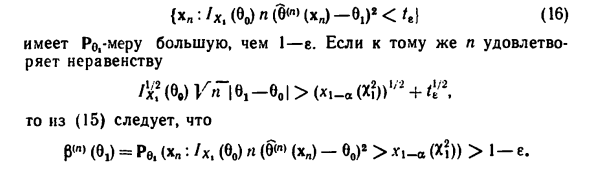


Скалярный параметр
- Изучите асимптотические характеристики повторяющихся выборок Критерий отношения правдоподобия введен в § 21§5 Альтернативы являются сложными, предполагая, что нулевая гипотеза проста Сложно: # 0: 8 = 80, I ^ bev, в = {60} и1 Параметр 8 является скаляром. Получить статистику по критерию в следующем формате (X „) = L <«> (x „; b * (xJ) / LM (x„; 256 (^ (n) (xn) — оценочное значение уравнения правдоподобия p ^ Модель (I?, 3S, {Re, 8e6}). считать Условие регулярности (A) — (D) §6§23 Уникальный (вероятность Пе, как правило, унифицируется как n — * — oo) Последовательный корень уравнения правдоподобия 8 (x„;.%)
Число (8 <«> (x„) — 80) + -1-dCh ™ (x „; 80) / (x ) — d№ (xn; QJ / dQ (№ (xn)%), A, «5! (X „; in” (xn)) / dv-d1M (xn; in) / (x ^ -00) + ^ -W» (xn; 84) / a83F «» (x „) -80) с, B) Где | e «—6o | <: | 8 (Xn; her» (xn)) / av = 0 И заменить производную формулой d8 для dLn> (x „; 80) / B В А), 1n <<)) (xn) = -1 / 2 // C) (xn; ej / de * (in <)) (xn) -80) «+ 2r ((xn), C) См. (C7), C9) §23) для оставшихся 2rn (xn) L MX „I <-y.h (X№n4Xn) -% \ (Vn @ * n) -W2-0 D) «Я когда п — »- оо. Используйте законы большинства и асимптотики Нормальность оценки 8 (x „) гипотеза X12 Халатность лаз. Знание приблизительного распределения статистики По стандартам большой номер Большое значение в критической области
Базовая статистика: {xn: 21pGS) (xn)>. g, _a (X?)} F) Xe (Xi2) — квантиль распределения xi2-размера эталона F) 257 Людмила Фирмаль
Увеличение n имеет тенденцию быть. Критерии F) статистика Замените большое n на статистику E и получите критерии в виде {x „: -dHY (v, QJ / dQ * (in <«> (x „) -80) r> *, -« (XI)}. G) Тогда используйте отношения -L Да (X „; 80) / (xn)) n @ («) (xn) -%) *> * i — «(X)?)}. (9) Использование выражений (см. C7), C2) §23) 8 >> (КП) -00 = — <Э / <«> (ХП; 8„) / де№> (Х „; в ^ / дб») — »х xA ^ rn (Xn, b0)), где rn (Xn; in) ^ 0, n-> oo, Опять же. У нас есть / l (b0) n @ «» (x „) -W- / l. (W) (y ^ qn (xn; c,) / 5vj’x x (J-a * / («) (xn; 9J / dWy * (\ + rn (xn;%)) *. A0) (10) Предпоследний фактор на правой стороне Для меры Re „to / A.’Chbo) мы получаем еще один критерий из (8). (Щ Практическое удобство критерия А1) состоит в том, что Приложение не нужно рассчитывать.
ТП 6f — oo имеют тенденцию объединяться как> n. рассматривать Давайте рассмотрим, как работает статистика F) относительно Po. время п — * — О. У нас есть 21n7-c) (xn) -2 (/ c> (x (n); Uhp)) — ^ »(x„; c,)) -: — + 2 (f <«> (xn; b,) — / <«> (xy; 80)). A2) Как вы уже знаете, первый член в A2) Гипотеза 6 = 8i верна, и существует крайнее распределение X12. Отсюда В частности, для любого ε> 0 и всех Большая л Re, (x „: № (X„; 6 «» (x „)) — / <«> (x „; 8J)> 0)> 1st.A3) К следующему L (‘(N) (; 8) / «» (6)) iJ] l (/ (8) // (x ;; 80)), И с тех пор (см. §22, отношение A7a) o = Mw | 1n (/ (X1; ej / AX ;; 80))> 0, тогда n-i (/ w (Xn; 8) — / <«> (Xn; 80)) — a> 0, n- + oo. снова
- Таким образом, при ε> 0 и всех достаточно больших η, Re, (xn: x- * (/ <«) (chl; b,) — / <«> (xn; b0))> a / 2)> 1. A4) От А3) и А4), п достаточно большой P (l) (9i) = Pe, (x „: 2 In» «) (x„)> x, _a (x?)) ^ ^ Pv, (xn: 2 (/ <«) (x ^ bO- / <«) (xn; 90))> pa) -e> 1-2e. Таким образом, для простых альтернатив 6, таких как Po, m> Pe … Степенная функция критерия F) имеет тенденцию унифицироваться как n — * — oo. Это свойство критерия называется платежеспособностью. Владелец — Все остальные критерии G) — (9), A1) также действительны. Действие Фактически для критерия (8) Vn (w) (x „) -80) = Vn (B« »(xn) -8,) + VT (8, -8 ,,). A5)
Это набор, начинающийся с n (B «Cxn) -8, J (X, _a (X? »L / a + tT, Потом из а5) P (n) (9i) = Pe, (xn: fx, (b0) n (§ »•) (xn) -b0) *> r, _a (X ^))> 1-e. 259 Эффективность критерия (9) аналогичным образом подтверждается, когда: Примите это во внимание / x, (e (x) (Xn)) — / x. (OI), снова Легко установить согласованность стандартов G) и A1). Вы можете сравнить непротиворечивые критерии, изучив следующий порядок Рядом с различными 8 силовыми функциональными блоками. Сравните их с работой функции в точке 0 = 8P, как показано ниже 8 «-» — 6’o, n — * — oo. Асимптотически эквивалентные критерии Вообще говоря, для ошибок i — »- oo критерии не равны Второй вид.
Первый член справа от A5) асимптотически нормален N @, / x, Fj)) как Re. Следовательно, если ε> 0, т> 0. Людмила Фирмаль
Это можно легко обнаружить, например, сравнив Критерии для критериев (8) и (9): тот же термин n ((T (m |) (xn) -фактор fx, (0), (8) и множитель Вблизи / х (8) относительно Pe (9). Обратите внимание, что статистика по критерию А1) является четверной Статистика квадратов локально сильнейших и односторонних Односторонняя альтернатива стандарту §4§21. Локально, самые строгие критерии существуют, только если В исключительных случаях компромиссная зона А1) Считается близким «оптимальным» между двумя странами Альтернативы.
Смотрите также:
| Векторный параметр | Векторный параметр |
| Оценивание параметров сдвига и масштаба | Полиномиальное распределение |

