Оглавление:


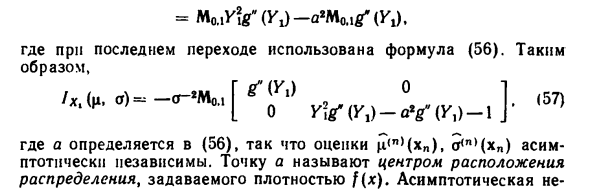




Оценивание параметров сдвига и масштаба
- Найти Фишер Информация Матрица Формула Повторная выборка из семейств плотного сдвига crlf ((x- | x) / o) и f (x) известны. Если g (x) = \ nf (x), / <«> fa; | i, a) = -a + g (fa-t) / a), = —A〜1 —a〜2 (xk- dCh / d \ 1 * = o ~ * g «((d = a ~ 2 + 2cr3 fa-t) g ‘(fa- = ar- * gr ‘((xt- | i) / e) + a-8 fa- \ i) g «(fa- Указывает, что e нормализовано по Y \ = (X-μ) / o. с. И учитывая какие X1; с 0 = мл << >> (X ;; ,, o) / Aj = 0 — ^^ A + a-1 (Xt- \ i) g ‘((Xt-)) / o)). Мы получаем Система уравнений правдоподобия ? G ‘((** — C) / <«) = 0,? A + O-1 (xf-)) Г’ ((x, -ц) / c)) = 0 253 В общем случае вам нужно решить это численно.
Оценка уравнения Вероятности q (n) (xn) и (n) (Xl) асимптотически нормальны w2 ((n, o), (f , (ts.o) i)), где fx.Oi, a) определяется по формуле E5). Асимптотическая ковариационная матрица Оценка зависит только от параметра а. Если плотность f (x) симметрична относительно нуля: / () = — / (- *), G (x) = g (-x), g ‘(-x) g’ (x), g «(-x) = g» (x), Откуда Mo.1U, 4G (Y) -0 Следовательно, матрица f *, (μ, o) и матрица Диагональ поэтому двумерная ковариационная матрица Нормальный вектор для ограничения случайного вектора Диагональ или ограничение нормального распределения
Распределения соответствуют независимым компонентам. Людмила Фирмаль
В этом случае Говорят, что оценки η (η> (Xn) n ° ((‘(Xn)) асимптотически независимы. Измените начало координат, если плотность f (x) является асимметричной Может считать и инвертировать недиагональные элементы матрицы / \, (8) В ноль. Я вижу iYi) E6) Введите новую параметризацию, установив j (x) = f (x + a), g (x) = * = \ nj (x) = g (x + a) и повторная выборка x \, …, xn От A до lJ от распределения ((x-μ) / a). M ,,,,, операция Плотность до 7 ((* -м) / ° К Мы получаем олк,? (K,) = VL ^ xYjT Wi) = Мо., ((^ -A)? (K, -a)) = = Мо., (Kt-a) f [(Kx) = M0AYlg «(K,) — aM0Ag» (KJ = 0, ,) = M_.i? (U,) = Мо.1? (К, -о) = Мо, i / (YJ, ,) = JVU.iV ?? (^ x) = mol (yk-bI? (Kt-a) = Последний переход использует уравнение E6).
- Так дорога Здесь a — это оценочное значение c, потому что a определено в E6). (N) (xn) и (n) (xn) являются асимметричными Асимптотически независимый. Точка А называется центром локации Распределение определяется плотностью f (x). Асимптотический не 254 Оценочные зависимости q (n) (xi), o (n) (xn) облегчают их использование. В частности, расчет асимптотических доверительных интервалов. Условие регулярности (D) (точнее, его вектор Аналог) Это слишком ограничительно
Поскольку a — * — 0, плотности от a до lf ((x- \ i) / a) имеют тенденцию быть бесконечными Бесконечность вблизи точки x- \ i сходится в µ и от l (x \ µ, a) — \ n (o ~ 1} ((x-μ) / o)) неравномерно становится μ, Там нет функции A (a-). Но Параметры неравенства | p, | -C:. > 0, c1, c2 являются необязательными Любая константа, и не более сложная для меня. с1 сколь угодно велико, с2 Если сколь угодно мало, сужение параметрической области не является обязательным с точки зрения применения.
При рассмотрении модели и диапазона параметров — oo <| d <+ oo, кт> 0. Людмила Фирмаль
Давайте посмотрим на некоторые примеры. Повторная выборка из нормального распределения в (II) Получите плотность a ~ 1y ((x-μ) / cg) g (x) = Inφ (x) = -In] 1π-x * / 2 g ‘(x) = -x, Оценка максимального правдоподобия \ i = x, a = = 1 / -V (* <- ~ x) r (см. Пример (II) в § 20) и их асимптотика G «Я Какие ковариационные матрицы равны E5) 1 0 О. М. φ (σ) = (T2, равный φ (σ) = σ2) является асимптотическим. Дисперсия (φ ‘(c) J DJl, c2, где o, c * — Любая положительная константа. При повторной выборке из гамма-распределения с использованием (III) Известны форма параметра p и плотность f (x, q, a) = = 0, 255 Может нарушать условие производной плотности f (x, µ, a) Нарушается в точке μ = x. Принимая р> 3, второй Возможность изменить вторую производную (условие (A)) и порядок
Порядок дифференцирования по параметрам и порядок интегрирования для .v ( (Состояние (B)). Условие (C) также выполнено (см. § 19) А5) и позже). Предполагая, что p> 4 при ограничении, Область параметров изменена на | (.i | -c2> 0- Условие (D) также выполнено. Мы видим (C), D) §7) g (x) = -1nG (p) + (p-1) lnx-x, g ‘(x) = (p-1) / x-1 g «{x) -.- (p- ) lx \ Мол / (Yx) = Мо., (- (P- ) IY ) = -1 / (р-2), Mo.iK, / (Yi) = -1, MoL / (K,) = — (p-1). Асимптотическая ковариационная матрица mp ) -1 1 р \ 2 «[-1 (р-2) Когда источник перемещается в центр распределения распределение
Смотрите также:
| Асимптотическая достаточность | Скалярный параметр |
| Векторный параметр | Векторный параметр |

