Оглавление:





Уравнение состояния Ван дер Ваальса
- Уравнение состояния ван дер вальса Форма уравнения состояния в единице дер Ваальса имеет вид Р = <11.ЗЗ.) в-B и 1 Где A и B-константы. Для неидеальных газов l /(v-b)может быть расширен степенным рядом b / u. (b / u) игнорируют члены более высокого порядка, начиная с 2y +(1.34)
Если сравнить эту формулу с(11.14), то 2-й вириальный коэффициент равен Температура кипения при которой исчезает B определяется следующей зависимостью: т° = ш — (1136> в. пт^,(— В-НБ Тира<1137> = P (T, V, n)-риртин — — — — — — -. (11.38)) Теперь можно определить все термодинамические особенности газового вала дер Ваальса.
Формула для свободной энергии ван-дер-Ваальского газа может быть получена путем замены (11.33) на (11.7). Людмила Фирмаль
Энтропия равна (11.39).) т. к. Энтропия идеального газа при тех же T и V равна наблюдаемой энтропии газа минус riR в (I «- nb)/ V. Когда выражение (11.35) подставляется в (11.19), n? Это явное противоречие объясняется тем, что при поиске 2-го вириального коэффициента мы игнорировали термин, содержащий bf V в большей степени, чем первый. Используйте уравнение Гиббса-Гельмгольца, чтобы найти внутреннюю энергию газа (11.40))
- Что касается теплоемкости при постоянном объеме、 (11.41) То есть газовая шахта derwurth имеет ту же теплоемкость при постоянном объеме, при той же температуре, что и идеальный газ. Все уравнения состояния, давление которых линейно связано с температурой, приводят к этому результату. Это можно просмотреть в общем формате на основе отношения (см. (4.2)) 1 / dSu \ _ _ & S 74-W) t-dVdT ’
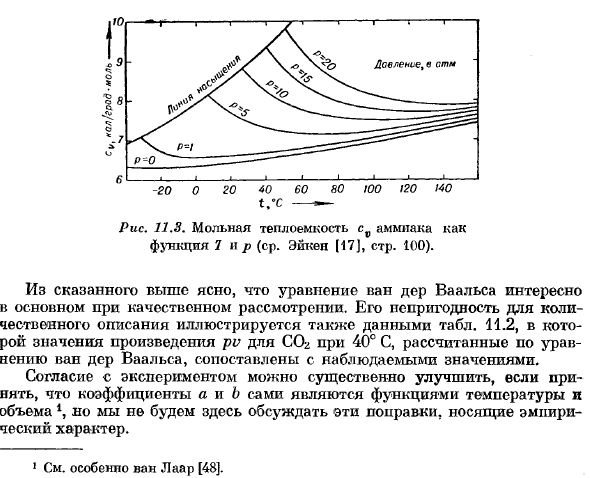
Используя первое уравнение(4.38)、 д соб \ _ Д Ф ДП \ «dfVdV)т -’ ДТ \ ДТ).y (ти-(с)、 (14.42) для всех уравнений состояния, где давление линейно связано с температурой、 врпэ. — ^=0.(11.43)) Однако на практике реальный газ ведет себя не так, и его теплоемкость не равна теплоемкости идеального gas. As на примере рисунка 11.3 показана зависимость молярной теплоемкости аммиака от ТНВЭД. Рис. 11.8. Теплоемкость молярная ЧВ аммиака как функция 7 и P(Айкен(17), стр. Посмотреть 100). Из вышесказанного ясно, что уравнение Ван-дер-Ваальса интересно главным образом в качественном рассмотрении.
Его несоответствие количественным заявлениям также указывается в данных таблицы. В пункте 14.2 значение pv продукта CO2 при 40°C, рассчитанное по формуле Ван-дер-Вааля, сравнивается с наблюдаемым значением. Если предположить, что сами коэффициенты a и b являются функцией температуры и объема 4, то согласие с экспериментом значительно улучшается, но мы не будем обсуждать здесь эти поправки, которые на самом деле являются эмпирическими. 1 см., в частности, van Laar [48]. Равновесие ван-дер-Ваальса можно легко распространить на двухкомпонентную смесь.
Для атомов коэффициенты a и b являются функциями 2-го порядка молярной фракции а-а \ х \ + а ^ р、 2 2 я) — bxx я + 2В \ 2xxx2 + b2X г. Таблица 11. 2 *(при р; с. М9-л, в * пр) В ПВ(приблизительно) ПВ (гребень) 1 25574 25597 10, 24485, 24713. 25 22500 23060 50 19000 19750 80 9500 10700 100 6930 8890 200 10500 14100 500 22000 29700 1000 400 (X) 54200 * Вода Ван Лаал[48]. Коэффициент а \ 2 характеризует силы взаимодействия между неравными молекулами. Лондон2 показал, что с первым приближением o^ это можно записать как: (11.45) „12 = Y“ 1 » 2 Кроме того, в грубом расчете коэффициент, связанный с объемом, занимаемым самой молекулой, можно рассматривать как линейную функцию молярной доли.
Б = адррес bxxx + 1)2×2. (11.47)) Эти упрощенные уравнения легко распространяются на системы, содержащие более 3 компонентов, поэтому они будут использованы в следующем разделе. Более подробное обсуждение пределов применимости уравнения ван-дер-Ваальса читатель может найти в работах Больцмана3 и Рокарда4. (11.44)
При этих упрощениях коэффициенты a и b газовой смеси могут быть представлены в следующем виде: Людмила Фирмаль
Смотрите также:
| Реальные газы. Расчет термодинамических функций по уравнению состояния. | Влияние неидеальности газа на химическое равновесие. |
| Вириальные коэффициенты. | Летучесть реального газа. |

