Оглавление:


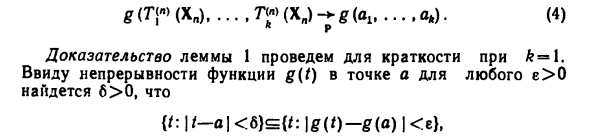


Состоятельность
- Различные методы оценки, с которыми мы столкнулись В предыдущей главе вы можете сделать следующую оценку Γ (xn): Любой размер выборки р. Оцените свойства при увеличении n Мы исследовали систематически. В этом пункте Краткое описание некоторых общих свойств приближения. Появляется в модели независимой выборки, повторенной в л -> — О. Подчеркнуть зависимость статистики T (xn) от n Для параметров используйте вместо этого под обозначением << η> (x „) 7 «(x„) вместо.
Предположим, что для каждого η статистика Γ (n) (xn) определяется путем измерения Измеримое пространство (/? «,? ™), n = \, 2, потому что мы говорим О бесконечных экспериментах Major P («> on (/?», Π), i = 1, 2, …. Я согласился. В этом случае из последовательности (/? «, Bn, {P (n)}), i-1, 2, …, вы можете перейти к интегрированной статистике Статистическая модель (80, I, {P}), SB состоит из бесконечных последовательностей
Последовательность x = (* i, X2, …) (подробности см. В разделе 1, §22) и Рассмотрим статистику 7 ((n) ([x] n), где x Сегмент [x] „= (* 1 x„). Людмила Фирмаль
Этот подход очень важен Вероятность, и на самом деле не играет такой большой Роль в статистике (за исключением статистики Статистический анализ). Тем не менее, мы одиноки Статистическая модель (8B,? 8, {P}) Возможные эксперименты и математическая ясность. Подчеркните, что все последующие соображения сохраняются Предполагая, что это принято во внимание, его значение полностью Последовательность модели (Rn, Bn, {P (n)}), таким образом Замените символы вероятности P и P (n) (соответствующими n). Используйте обозначения для упрощения расчетов отрезки x „бесконечной последовательности x = (xt, …, xn) = (* I, * 2, …) эй? ,
Определение 1. Для каждого η = 1, 2, … Статистика 7 » (x„) (или, короче говоря, приблизительно 7 » (x„)) Любое e> 0 и любое P {P} P (xn: | 7 «<«) (x ,,) — 9 (P) |> e) -0, n-oo. A) В параметрическом случае вместо А) Pv (xl: | GS) (xn) -p (c) |> e) -> 0, n-oo, e <= c. B) Для векторной статистики T (n) (xn) и вектор-функции φ (9) (Или φ (P)) согласованность связана с B) (или А)) для каждого компонента. Они говорят, что если А) имеет место для фиксированного P Последовательность съел. с. 7 » 0. р Согласованность Разумный класс 7 «<«> (x „), и должен быть представлен для всех классов О модели пересэмплирования, которую я встретил ранее, Богатый ..
- Вспомните несколько примеров. E. F.p. Fn (x; x „) -согласованная оценка теоретического f. F (x) в любой точке x. Примерная последовательность моментов (Среднее, дисперсия и т. Д.) Может быть легко получено на основании: Следующие два утверждения. Теорема Хинчина ([2, т. 1, гл. X, §2; т. 2, гл. VII, § 7]). Xt, i = l, 2, …, являются независимыми последовательностями Равномерно распределенная ель. с. И NiXt = μ, конечно Bom E> 0 Лемма 1. Каждая последовательность ели. с. 7 «, (HP), / ‘= 1, …, k, постоянная a с вероятностью a / G g (U, …, tn) — непрерывная функция в точках (c1, …, ak). g (T <>> (X „), …. 7 Вт (X„) — * g (a, ak) .D)
Однако последняя вероятность согласно А) равна n- + -> оо | Образец квантиля X [«P],», 0 nl)>, где хк, пшкХ (к) -к-й порядок статистики х „наблюдаемого вектора, Является ли последовательная оценка теоретического квантиля XP. Предположение, что уравнение p = F (x) имеет единственное решение При решении x = xP функция F непрерывна в точке xP. Докажи первым Это утверждение для повторной выборки из униформы в @, 1) Распространение.
К П Доказательство леммы 1 выполняется для краткости 6 = 1. Учитывая непрерывность функции g (t) при a для любого ε> 0 б> 0, {t: \ t-a \ <6) c = {t: \ g (t) -g (a) \ (xn)) - g (c) |> e} (xn) -c |> 6}). Людмила Фирмаль
Из леммы 2 § 5 для Xlt …, Xn ^ i- Индекс независимости G (X, 1), S * = A ^ i + … +. X *, фут = 1, … n + 1, затем эл.в. Zft.n = Sft / Sn + i, ft = l, …. n, E) Распределяется как статистика заказов для повторной выборки из @ Равномерное, 1) распределение. Применяя великий закон Числа у нас есть Sn + i / (n + 1) — * — k, SmPil [np] — * — I ,, n — »- oo, Оттуда, используя лемму 1, [pr] in + int + 1 p Здесь F (x) непрерывно. r Общий вид. предположение F-l (z) = sup (x: F (x) -z), Xi = F ~ l (Zi), i = l, … …. n + 1 — повторный выбор из распределения Распределение F (x), F-x (Zk, n) —Xk, n. Используя лемму 1, G) F (х)
Смотрите также:
| Последовательный критерий отношения правдоподобий | Состоятельность оценок максимального правдоподобия |
| Среднее число наблюдений в последовательном критерии | Асимптотическая нормальность |
Если вам потребуется заказать статистику вы всегда можете написать мне в whatsapp.

