Теплоемкость идеального газа, химические постоянные.

Теплоемкость идеального газа, химические постоянные.

• Идеальная теплоемкость газа. Химические константы Теплоемкость идеального газа тесно связана с его молекулярной структурой.Точное соотношение было выведено на основе статистической механики, но здесь дается общее описание задачи.Более подробное изложение можно найти в руководстве по статистической механике. Предел, если средняя энергия молекулы равна сумме энергий поступательного, вращательного и колебательного движений.Теплоемкость при постоянной мощности cv (см. 10.5) также состоит из 3 элементов по этим 3 видам движения. 1 Фаулер[191, Гл. III;Фаулер и гуггебейм[20], гл. III; Майер и Майер [34], гл. В — ‘ ВОСЬМОГО.

Поступательная составляющая удельной теплоты равна 1 / J \на молекулу, а вращающаяся составляющая равна R или 3 /?В N это зависит от того, является ли молекула линейной или нет.Последнее описание является точным только в том случае, если вращательное движение может быть описано классическим (неквантовым) методом mechanics.In во всех случаях, за исключением очень легких молекул (II2 или III), классического приближения достаточно даже при низких температурах.Наконец, вклад в Удельную теплоту, обусловленную взаимными колебаниями атомов в молекуле, представляет собой сумму вкладов от различных типов колебаний.

Каждый вид вибрации характеризуется собственной частотой Людмила Фирмаль

Удобно выражать собственную частоту по отношению к характеристической температуре (Oj), определяемой соотношением. =(С. 13.） Где h-постоянная Планка(h = 6.624 X 10-ii7 ope-s), k-постоянная Больцмана, деленная на число авокадро(N = 6.023 XX 1023; k = 1.380 X 10-1C erg * deg-1); следовательно, h / k = 4.80 X 10-degsec.

Вклад каждого колебания в удельную теплоемкость возрастает с ростом температуры и может быть описан в виде RP(T I Sj).Где P-универсальная функция, называемая функцией планка-Эйнштейна.Ниже приведена краткая таблица этой функции. 1 А У .- Я и с КЛ если.Я… Функция планка-Эйнштейна* t / E V * 1 2 фута П(Т / 0)0.022 0.303 0.724 0.928 0.979 0.9995 Все таблицы 1 (T / W)N. S. Taylor и S. см. Classo-ne. L бумага, Физическая химия, т. I (3-е изд., Лондон, 1942) Приложение I [ср.Х. Карапетянц.Химическая термодинамика.Добавление 3. М.-Джи. Гхи, 1953.(Приблизительно.）\ При высоких температурах(то есть больших T / 0) эта функция имеет тенденцию совпадать, и вклад в молярную теплоемкость каждого типа колебаний имеет тенденцию быть R.At при низких температурах функция P стремится к нулю. Итак, колебательную составляющую удельной теплоты можно описать следующим образом: С ‘(Т)= K2P(-|). (10.14）

• Внутри таблицы. 10.2 показывает значение 0 для некоторых двухатомных молекул. Полученные результаты можно обобщить в следующем виде: СР = СР(0)+ ХГ(Т), (10.15） Таблица 10.2. Cp (0)= 5/21 \длина одноатомной молекулы; = 7 / GK для линейной молекулы; Cp (0)= 4R для многоатомной нелинейной молекулы. Заметим, что квантование вращательных степеней свободы больше нельзя игнорировать, поэтому уравнение (10.15) нельзя использовать вблизи абсолютного нуля температуры. Поскольку функция планка-Эйнштейна мала при низких температурах,она может определять определенную температуру, т. c ‘(T)= 0 при T ми°〜 О2 2250 Бк2 470 N2 3350 J2 305 Нет, 2710 МЕ С100. Перейти Тао I1G1 42SU CI, 810 II Br 3560 Вода Айкен[17], стр. 151. = Т *(0) ж) п р + 4С (т) ДТ-РТ_ л кг К-М> М Ж I \ T (10.17） ч(0)= К(К) — СР (0)в; с(т0,Р0) — СР(0) — СР(0)1П т0 + H в ПО Р Куда? (10.18）

Количество / химическая константа этого идеального газа называется. Значения & (0) и / указывают на то, что To меньше T температура, определенная в (10.1 B) и (10.15), не зависит от выбора T0 и po, если она выше температуры, которая была бы неточной из-за квантования вращательного движения молекулы. Прежде всего, обратите внимание, что все t0 меньше T1, но при изменении интегрального значения (10.17) интервал интегрирования может быть расширен до 0°K.So, выражение(10.17) можно записать в следующем виде: m(T,p)= h(To) — Cp(0)T0-T [s (To,po) — cp(0) — s, (0)в Tc + + R в P0] — Cp (0)t в T + 5 S ‘ (T) dT-T 5 ^ D T + NAT. (10.18 ‘） о’о’о’ * Выберите другое начальное состояние T±y pi вместо T0, p0.Тогда, если Tt меньше T ‘и выражение(10.15) находится в допустимой области、 И(т,п)= ч(Техас) — СР(0)Т — Т [с (ТП) — СР(0）- т. — Cp(0) в Ti + R в pj — (0) Tin T + ^(T) dT-

Количество / химическая константа этого идеального газа называется. Значения & (0) и / указывают на то, что To меньше T температура, определенная в (10.1 B) и (10.15), не зависит от выбора T0 и po, если она выше температуры, которая была бы неточной из-за квантования вращательного движения молекулы. Прежде всего, обратите внимание, что все t0 меньше T1, но при изменении интегрального значения (10.17) интервал интегрирования может быть расширен до 0°K.So, выражение(10.17) можно записать в следующем виде: m(T,p)= h(To) — Cp(0)T0-T [s (To,po) — cp(0) — s, (0)в Tc + + R в P0] — Cp (0)t в T + 5 S ‘ (T) dT-T 5 ^ D T + NAT. (10.18 ‘） о’о’о’ * Выберите другое начальное состояние T±y pi вместо T0, p0.Тогда, если Tt меньше T ‘и выражение(10.15) находится в допустимой области、 И(т,п)= ч(Техас) — СР(0)Т — Т [с (ТП) — СР(0）- т. — Cp(0) в Ti + R в pj — (0) Tin T + ^(T) dT- (10.18 «） — Т ДТ + РТ] Я \ С. О Формулы (10.18’) и (10.18») определяют одинаковое значение реки.Если приравнять правую сторону, то она выглядит так: ч(т0) — СР(0)т0-Т [α(т0,ОО) — СР(0) — СР (0) — СР (0) в т0 + + р на Р0] = ч (ти) — Ср ^ ти-Т — [8 (тир) — резюме(0) — П(0)в 7 \ РНК РЖ,]. Это соотношение может быть соблюдено при всех температурах только при следующих условиях: 1) h (To) — cr(0) T0 = h(T) — Cj>(0) T, то есть если η (0) не зависит от выбора To, и 2)С(К,П) — СР(0) — Ср(0)1n7 )+ Spn0 = с(Thpi) — СР(0) — резюме(0)lnTi-Ф в ФОП

То есть, если/не зависит от выбора Таким образом, значения r (0) и химических констант, определенных по формуле (10.18), не зависят от выбора T0 и p0, если T0 находится в указанных выше пределах. Величина/’, очевидно, зависит от выбора единицы давления, в которой обычно используется атмосфера. Поскольку мы по существу предположили, что теплоемкость газа в интервале температур от 0 до T0 постоянна и равна (0), ТО & (0)имеет значение энтальпии газа, экстраполированной на абсолютный ноль температуры. Выражение (10.17) можно переписать в более удобную форму, применив преобразование(4.20). Т. Т. -В t-1 5-5 c ‘(t) dT-j] + В V, (10.19） ч(0) _ СР(0） К Т Р ИТ О, да. смотрите откуда (10.11） ИТ / ХТ <7)= ч(0) — СР (0) тг—$ <ф (т) dт-й \ т. (10.20） 0 0

• Термодинамика позволяет ввести понятие химической постоянной, но не дает способа определить ее численное значение.Однако она может быть рассчитана с использованием статистической механики для установления связи между химическими константами и молекулярными структурами. Один атом газа В этом случае уравнение、 r = gzbz = _ 1-587 + 41el / + 1 » g — <10-21） В этом уравнении M-молекулярная масса газа, а∞ — числитель самого низкого квантового состояния (основного состояния).Статистические веса могут быть найдены из спектроскопических data.So спектроскопически мы обнаружили, что основное состояние инертного газа является состоянием статистики 1.

Основное состояние пары атомов щелочного металла、 Который l o = 2. Внутри таблицы. 10.3 показаны химические постоянные значения некоторых одноатомных веществ.Значения в столбце 3 таблицы описаны ниже. Таблица 10.3 Химический состав ( / ) N постоянное давление паров некоторых одноатомных элементов (/’）* Элемент j’g’ №.-0.08 +0.37 -0.02 г±0.065 Нэ + 0.390 + 0.04 АР +0.81 + 0.79±0.04 НД +1.80 + 1.95 + 0.00 К +1.10 + 1.11±0.3 На 4 0.75 +0.854: 0.15 Компакт-диск +1.49. 4, 1 / 2, 0, 10. ЗН +1.18 + 1.15±0.05 РВ +1.88 +2.27±0.30 АГ +1.45 + 2.10±0.40 КР +1.11 + 1.00±0.40 Мг +0,49 + 0,44±0,10 * Water ainen[17J, p. 285. Двухатомные и многоатомные линейные молекулы Для молекул этого типа статистическая механика приводит к уравнениям о р / = -3.185+ -] г(10 «> /)+ войти.(10.22)） Зо.

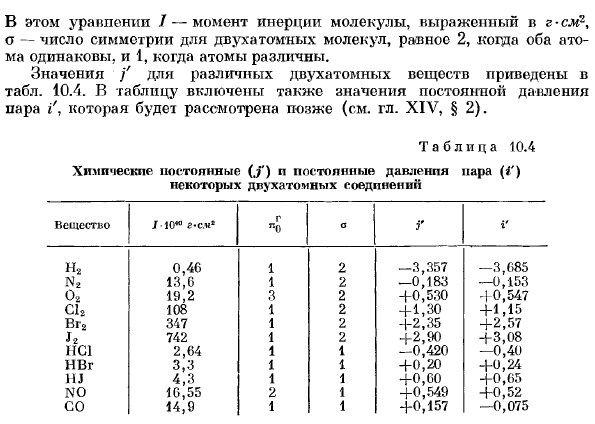
В этой формуле/- момент инерции молекулы, который выражается в г см2, где о-число симметрии 2 атомных молекул, и 2, если оба атома одинаковы, и 1, если атомы различны. 10.4.В таблицу также включено значение постоянного давления пара i’.Мы рассмотрим это позже(см. XIV,§2). Таблица 10.4 Химические константы некоторых двухатомных соединений(.»; «) N постоянное давление пара(/ ‘） Вещество/!0 * °г-см * г «0оГi ‘ Н2 0.46 1 2 -3.357 -3.685 Н.* 13.6 1 2 -0.183 -0.153 О2. 19.2 3 2 +0.530 +0.547 С12. 108 1 2 + 1.30 +1.15 Тема vg2. 347 1 2 +2.35 +2.57 Н. 742 1 2 + 2.90 +3.08 НС1 2.64 1 1 -0.420 -0.40 Тгг. 3.3 1 1 +0.20 +0.24 HJ. 4.3 1 1 + 0.60 +0.65 Ч0. 16.55 2 1 +0.549 +0.52 14.9 1 1 +0.157 -0.075 Нелинейный полинуклеотид

Значения f различных двухатомных веществ приведены в таблице. Людмила Фирмаль

В этом деле Около 1 г Г= _ 3,735+ — ЛГМ + 7] г(10 ‘ ^ / а / £ / с)+ войти,(10.23） В <Л(Г Где / a, J и J c-основные моменты инерции молекулы. o-число, определяемое симметрией молекулы. В заключение, дифференцируя уравнение химического потенциала (10.17) относительно температуры (см. (0.27)), получаем формулу энтропии идеального газа.Поэтому можно рассчитать энтропию газа, используя только те, которые определены спектроскопически

Смотрите также:

Предмет термодинамика

Идеальные газы. Уравнение состояния идеального газа.	Смеси идеальных газов.
Термодинамические функции идеального газа	Химические потенциалы и химическое сродство в смеси идеальных газов.