Парадоксы и некоторые нюансы капитализации

Парадоксы и некоторые нюансы капитализации

Парадоксы и некоторые нюансы капитализации. Уравнение (1.1) означает, что капитал увеличивается в геометрической прогрессии с продолжительностью финансовой операции. Таблица предоставлена, чтобы проиллюстрировать природу этого изменения. 1.1.

• Однако давайте рассмотрим рост капитала, а не рост капитала, чтобы вы могли увидеть разницу между простым

и сложным процентом с одинаковой скоростью в течение определенного периода времени. Людмила Фирмаль

В этой таблице показаны пять вариантов ставок с полями, которые переопределяют часто используемые вилки ставок в Западной Европе, а также учитывается прирост основной суммы C = 100 в течение 20-летнего периода.

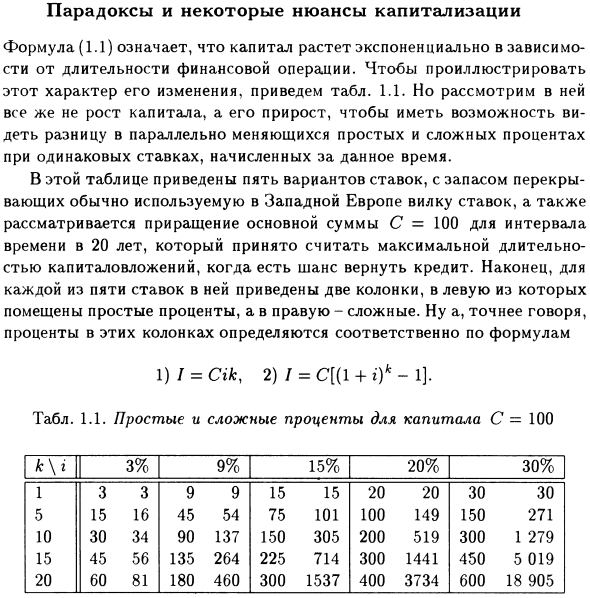
Это считается максимальным сроком инвестирования, если у вас есть возможность погасить кредит. Наконец, для каждой из пяти ставок включены два столбца, с простым интересом слева и сложным справа. Точнее, проценты этих столбцов определяются по формулам 1) / = Cifc и 2) I = С [(1 + 🙂 * -1] соответственно.

• Tab. 1.1. Простые и сложные проценты 3 капитала C = 9% 15% 20% 30% 1 3 3 9 9 15 15 20 20 30 30 5 15 16 45 54 75 101 100 149 150 271 10 30 34 90 137 150 305 200 519 300 1 279 15 45 56 135 264 225 714 300 1441 450 5 019 20 60 81 180 460 300 1537 400 3734 600 18 905 В этой таблице нет ничего парадоксального.

Сумма, полученная в уравнении (1.1), не удивительна, поэтому, если мы ставим те же 100 на 3% в год в течение 100 лет: 1882. Однако замена 3% на 30% потребует 2479 вдохов за те же 100 лет. -1013. Вы можете оценить

стоимость этой суммы, используя современную машину, которая насчитывает 100 счетов. Людмила Фирмаль

Предполагая одну секунду. Такая машина рассчитывает 10 билетов, поэтому видно, что пересчет всей суммы занял бы более 785 веков. Эту фиктивную кучу денег можно сравнить со всем золотом, которое добывали из-под земли за весь период его существования. При цене золота в 105 долларов за кг вес золота оценивается в 20–40 тыс.

Тонн, что говорит о том, что стоимость «горы» более чем в десять раз выше. Конечно нет. При нормальных ставках долгосрочная капитализация приводит к начальному капиталу и несоизмеримой сумме. Например, если бы Таблица 100 была размещена на каком-либо счете на 50 лет под 50% на 20 лет, получилось бы только 332 426%.

Однако такие ставки возможны только в условиях высокой инфляции, где обесценивание денег очень велико. И здесь мы можем продолжить наш разговор, начиная с раздела 1.1.1, о цене рисков, специфичных для процентов. Например, в случае войн или революций ссуды часто погашаются не полностью.

Риск крупных потерь также связан с рядом стихийных бедствий и катастроф (наводнения, землетрясения, катастрофы и т. Д.). В результате кредиторы становятся богаче, но не намного. Кроме того, кредиторам, как и другим экономическим агентам, предоставляется собственная доля национальных продуктов, даже при экспоненциальном росте на душу населения.

А статистика показывает, что такие показатели, как доля национального богатства, покрывающая интерес к цивилизованным странам, могут уменьшиться. Ну, главный нюанс капитализации касается нормы прибыли любой финансовой транзакции.

И это хорошая идея, чтобы узнать эту концепцию как можно скорее, чтобы лучше понять ее. Пример 1.4 5-летняя казначейская облигация, выпущенная государством в декабре 1969 года, была продана по цене 900 по номинальной стоимости 1000 и была погашена в срок по цене 1150.

Годовая ставка этой финансовой транзакции — какова доходность я? Решение. Легко видеть, что при постоянной годовой ставке i соотношение 900 (1 + g) 5 = 1150 должно быть выполнено. Отныне я = (115/90) * / 5-1 = 0,05025 *

Смотрите также:

Предмет финансовая математика

Сложные проценты.	Пять типов эквивалентных ставок.
Формула сложных процентов.	Две основные ставки.