Оглавление:








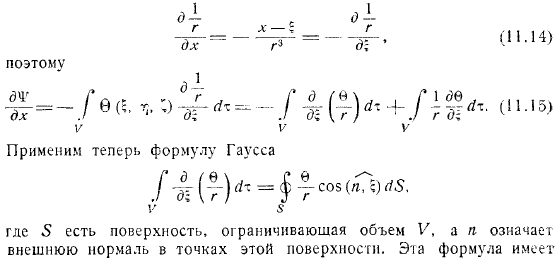

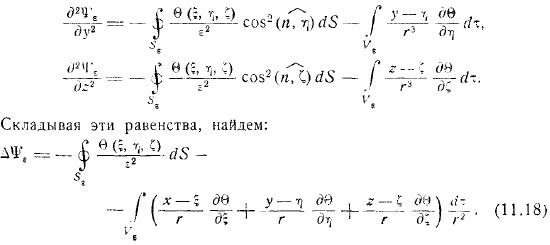

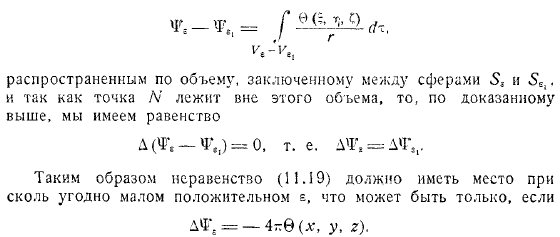



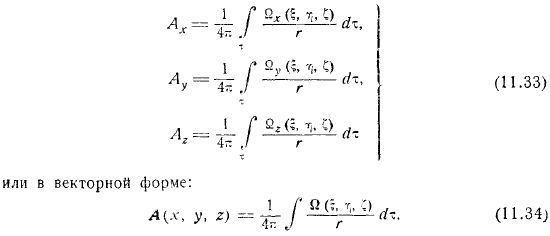



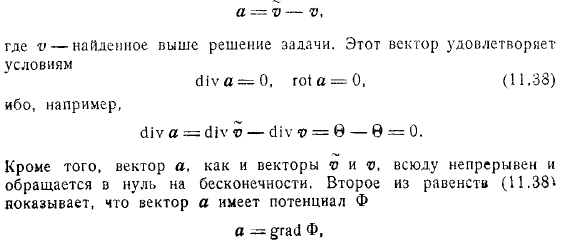


Вычисление вектора скорости по вихрю и расхождении о скорости для бесконечного пространства
Если поле скоростей движущейся жидкости задано, то вихревое поле определяется простой помощью дифференцирования составляющей скорости относительно. Другими словами, он представляет собой вихревой вектор. А, как известно гидромеханика, составляющие вихря суть, и столь же легко определить несоответствие данного. Обратная задача о расхождении с заданным распределением завихренности требует добавления дополнительных условий, то есть обозначения регулярной составляющей скорости поверхности, ограничивающей объем рассматриваемой жидкости, для определения скорости в любой точке жидкости для полного решения.
Учитывая, что жидкость заполняет все пространство и бесконечно стационарна, мы ограничимся рассмотрением простейшего. К каждой точке в пространстве задается скорость вихрь и скорость. Необходимо определить вектор скорости для расчетов, есть уравнение. Во-первых, мы предполагаем, что расхождение между скоростью внутри и вихрем равно нулю вне конечного объема. И их частичное.
Кроме того, предположим, что на плоскости разрыва нормальная составляющая вектора остается непрерывной и что только касательная составляющая этого вектора может быть прерывистой. Рассмотрим желаемую скорость как сумму скоростей и примеры образования вихрей. Существует скорость, соответствующая расходимости, и вихрь становится нулевым, и есть скорость, исходящая из вихря, и расходимость становится. Чтобы определить вектор, есть условия для определения вектора, и получены следующие условия.
Покалывает, что мы имеем дело с невращательными движениями. И как мы показали в начале этой главы, существует возможность. Мы присваиваем значение этого первому уравнению и получаем уравнение Пуассона для определения функции. Сначала приведем решение этого уравнения, которое имеет нестрогую, но простую гидродинамику. Кроме того, функция начала координат предполагает, что где угодно пуля равна, за исключением очень малой окрестности начала координат.
Здесь, согласно теореме Гаусса, заметим, что интеграл расходимости вектора скорости равен потоку вектора скорости через поверхность, ограниченную объемом, то есть поверхность, ограничивающую объем. Применяя эту теорему к нашему примеру, мы видим, что поток вектора скорости через поверхность, ограничивающую объем, должен быть равен. В крайних случаях, когда объем сжимается до точки, получается изображение потока, который находится в начале координат и вызван источником с силой или обилием, равным. Нетрудно найти формулу для этой схемы течения.
Из-за симметрии соответствующий потенциал скорости можно считать функцией только расстояния точки от начала координат. Однако, как показано, функция имеет сингулярность везде, кроме начала координат, и должна удовлетворять уравнению, записывая это уравнение в сферических координатах, дополнение долготы и широты которого любая интегральная постоянная должна иметь равное значение для потока скорости через любую сферу, центрированную в начале координат.
А так как нормальная составляющая скорости такой сферы имеет постоянную величину, а площадь сферы равна, то мы это сразу выясним. Кроме того, легко увидеть, что любая константа отбрасывается, потому что она не имеет существенного значения. Если сила источника важна, то получается следующая формула для соответствующего потенциала скорости: схема соответствующего потока достаточно проста. Линия потока-это прямой луч, исходящий из источника.
Скорость движения частиц жидкости направлена вдоль этих лучей от начала координат и имеет значение. Прямо пропорциональна силе источника и обратно пропорциональна мощности от расстояния до источника. Если имеется отрицательное значение, то запасы. В этом случае скорость движения частиц жидкости направляется в ту точку, где расположен слив. Вернитесь к решению уравнения Пуассона, разделите объем на меньшие объемы в каждом таком объеме, используя координаты, чтобы получить точку и поместить ее в изобилии у источника.
Тогда функция где расстояние от точки с координатами до точки. Очевидно, что в соответствии с вышеизложенным мы получим приближенное решение задачи. обнулить все объемы и получить выражение для функции. Этот интеграл распределяет источник по объему для решения уравнения. И формирование соответствующего потенциала для распространения этого источника. Здесь мы даем строгое доказательство того, что функция удовлетворяет уравнению Пуассона. Прежде всего отметим наличие ньютоновской.
В случае распределения в определенной области уравнение Лапласа заполняется точкой вне. Факт, если точка находится вне объема. Тогда интеграла. Поскольку он не исчезает, его можно дифференцировать относительно под знаком. В результате вы получаете, но вы можете легко увидеть, что это. Теперь рассмотрим случай, когда точка находится в объеме, и предположим, что функция непрерывна, то есть ее первая производная в этом объеме. Рассчитанный. Во-первых, функция под знаком интеграла превращается в бесконечность как. Вот почему этот интеграл принадлежит, как и в потенциале.
- Для неправильного числа интегралов этот интеграл сходится. Известно, что объемный интеграл сходится, когда подынтегральная функция падает до бесконечности на степень ниже порядка. Однако в этом случае подынтегральная функция является бесконечно большой порядка, и поскольку интеграл больше не сходится, то нет права выполнять дальнейшее дифференцирование по под знаком интеграла. Поэтому формула предварительно преобразуется. Очевидно, следовательно, где есть поверхность, которая ограничивает объем, и применяет формулу Гаусса, которая означает внешнюю нормаль в точке этой поверхности.
- Подынтегральная функция бесконечна как, но если выбрать точку с малой сферой радиуса, то интеграл на поверхности этой сферы будет на порядок больше и исчезнет на пределе, если он стремится к. В первом интеграле справа точка y находится внутри объема, и поскольку есть точка ,больше не исчезает .Интеграция выполняется. Если у вас есть какие-либо вопросы, пожалуйста, не стесняйтесь связаться с. Интеграл справа также представляет Ньютона. Теперь мы можем произвести снова.
Производная по отношению к под знаком. В результате. Существует и, кажется, только что был найден. Если есть шар с радиусом, центрированный в точке, он находится в точке ограничивающей сферы. Для таким образом, для мы также объединяем эти формулы, мы находим. Если абсолютное значение находится в точке шара. Если не превышен, то существует очевидная оценка. Следовательно, следует также отметить, что это и значение интегральной гаммы может быть легко вычислено. Оценка будет легкой. Но величина не зависит от радиуса шара.
Потому что если взять шара, имеющих общий центр в точках, и имеющих радиус, то разность в соответствующей функции черного шара представляется ньютоновским потенциалом. Объем, заключенный в сферы и расширяется. А так как точка находится вне этого объема, то мы имеем равенство, то есть неравенство таким образом, о чем свидетельствует. Это возможно только в случае то же самое уравнение справедливо для любого объема, который может быть разделен в любое время на шар радиуса вокруг точки и остальную его часть, так что равны, так и будет. Применяет результат к потенциалу, определяемому равенством.
При равномерном нагреве тонкого слоя силиконового масла, перемешанного с алюминиевыми хлопьями и разлитого на плоскости, можно получить тороидальные вихри, представляющие собой ячейки Бенара. Людмила Фирмаль
Внешняя точка объема, то есть точка, в которой расхождение равно пуле и равно, потому что это точка, объем, вектор. Это решение системы уравнений. Далее обратимся к определению векторов, удовлетворяющих системе уравнений. В этом случае, конечно, вектор и предполагается удовлетворяющим условию. Для всех векторов выполняется равенство a. Кроме того, как показано выше, в разрывах нормальная составляющая вектора должна оставаться непрерывной. Удовлетворяют первому уравнению.
Если положить, то здесь определяется вектор, называемый векторным потенциалом. Если мы присвоим это значение выражению, мы получим. обратите внимание, что в настоящее время существует следующий простой в проверке: компонент. Вектор, содержащий. Итак, мы получаем уравнение объявлений. Без потери общности. На самом деле, давайте найдем вектор, который выглядит так. Затем введите, чтобы найти и выбрать так, что проявляется следующим образом: равенства и уравниловки.
- Спасибо за условия. Уравнение. Упрощенный. Поэтому для определения вектора, мы получили векторное уравнение Пуассона. Это эквивалентно скалярное, решение которого находится в виде или в векторной форме. Теперь убедитесь, что найденный пример вектор соответствует. Другими словами, это случай одной вихревой нити. Да, запустите условие. Объем можно разделить на конечное число объемов. Каждый объем имеет непрерывную производную от по своим координатам. К каждому из этих томов можно применить выражения формы.
Добавьте эти уравнения и обратите внимание, что они обусловлены и условиями. В результате вы получите. Если добавить такое уравнение, которое применялось бы ко всем объемам, то оно выглядело бы так: однако условие, что непрерывность сохраняется при прохождении через разрыв, следовательно, интеграл берется на поверхности. Объемы, которые отделяются друг от друга, отменяют друг друга, и остаются только интегралы на поверхности, которые ограничивают объем, но компоненты на поверхности также исчезают в, потому что вектор исчезает за пределами поверхности. Пожалуйста.
Решение получено, и, таким образом, система достигает решения уравнения. Поэтому задача определения скорости по заданному распределению вихрей, когда вихрь и расхождение равны нулю, а расхождение для бесконечного пространства, имеет следующее решение вне конечного объема. Ели обозначить расстояние от точки до начала координат через, то ясно, что величина являются порядками, а производные этих величин по отношению к координатам — порядками.
Если вы наложите на искомый вектор требование, что он везде непрерывен и бесконечно исчезает, то легко показать, что найденное вами решение является единственным решением проблемы. Фактически, мы предполагаем, что вектор удовлетворяет всем требованиям. Давайте рассмотрим, где решение проблемы, которую мы нашли выше. Этот вектор удовлетворяет условию например, и далее, вектор, и вектор.
Исчезает непрерывно и бесконечно везде. Равенство указывает, что вектор имеет потенциал и находится от первого. Следует, что таким образом, является гармонической функцией, а также гармонической функцией и производной. Однако ясно, что гармоническая функция достигает своих максимальных и минимальных значений на границах области.
Если мы возьмем область внутри сферы большого радиуса с центром в качестве начала координат, то увидим, что значения всех компонент вектора должны быть меньше тех, которые стремятся к нулю в. То есть все составляющие вектора должны быть равны нулю. Вы можете освободиться от ограничения, что исчезает за пределами конечного объема. То есть, если бы были сделаны только некоторые дополнительные предположения, например, предположив, что она бесконечна, то можно было бы считать бесконечным объемом жидкости. Это порядок приоритета.
Эти ячейки возникают за счет тепловой конвекции, идущей от равномерно нагретой медной плоской поверхности вверх через центр каждой ячейки и затем вниз по краям контакта со смежными ячейками. Людмила Фирмаль

