Гамма-распределение

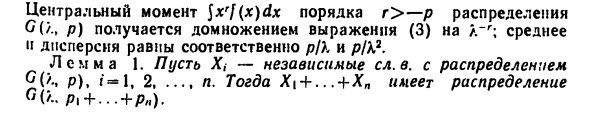
Гамма-распределение

• Стандартная величина задается формулой / (*) = Ю, * <о. где ж. 5 -Гамма-функция Эйлера, р-параметр, называемый параметр- Параметром формы. можно выбрать еще и масштабный параметр л. С (>., Р) для распределения с плотностью ер-1Э ?. дс) х> о. б) Центральные моменты распределения? 7А, р) равны -, г> -п. в) [| о Ы формулы A) интегрироваться по частям легко получить Г (р + 1) = рГ (р). D) Отметим также известную нз анализа формулу ГА / 2) =) ‘л. Принимая во внимание D), из C) G (л) ^ xf (x) dx = p, E) Iх р ~} х ~ р ‘ Центральный момент xr dx порядка г> —р распределения П (/., Р) получается домножением выражения C) на л ~ г; среднее »

Дисперсия равны соответственно р / К и р / К2. Лемма 1. Людмила Фирмаль

• Пусть Xt-независимые ел. С (/., Р), i = 1, 2 п. Тогда Х \ + … + Х коказательство. Достаточно рассмотреть случай и = 2. По формам у ви свертки ([2], т. 2) цифра ел. в. Х \ + Х2 означают при х> 0 / , — № () = Дж / мл. (O /.(— O * ‘ х ( J Сделано замененные значения s = xt, приведенное выражение для fxt + x, (x) к виду 1, то есть постоянный множитель с равенством 1 / G (р1 + рг) (см.А)), что и доказывает лемму при п—- 2. Отметим попутно доказанную формулу G)

Действительно, если р = п-натуральное число, то соответствует распределенная сумма как независимая распределением G (X, I) и применима центральная предельная теорема для одинаково распределенных слагаемых. к сумме добавляется еще одно G (K, р— \ р ), где \ р \ -целая часть р, которая асимптотически пренебрежимо.

Из леммы 1 вытекает, что следует при больших р Приближение нормальных и тех же средним и дисперсии. Людмила Фирмаль

Смотрите также:

Предмет статистики

Оценивание параметров экспоненциального распределения	Экспоненциальное распределение
Оценивание по первым г порядковым статистикам	Распределение х2 с п степенями свободы