Оглавление:


Критерии для проверки сложных гипотез
- Критерии проверки сложных гипотез Используйте пример выборки нормального распределения для анализа проблем, возникающих при проверке сложных гипотез. Пример 3. Получить независимую выборку (1) из нормального распределения с параметрами (a, o). Кроме того, это известно.
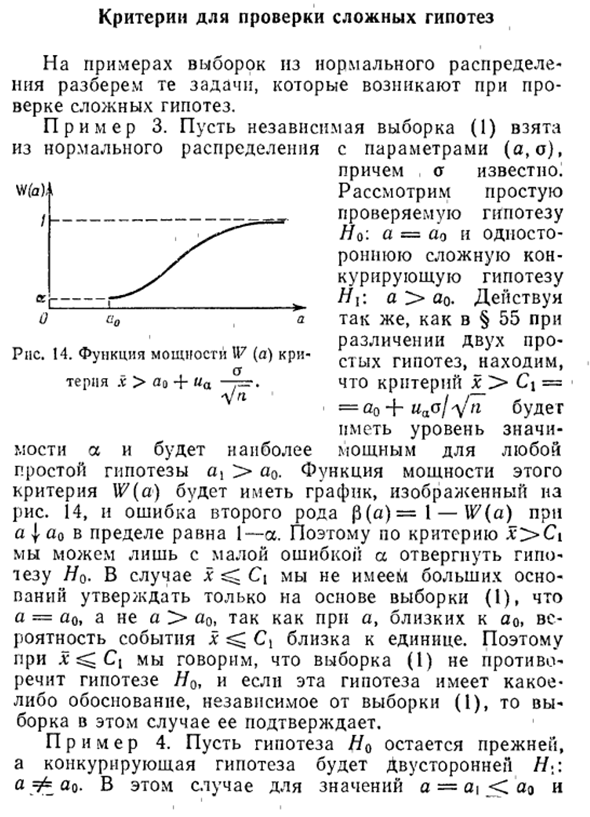
- Рассмотрим простую проверяемую гипотезу Ho: a = ao и одностороннюю комплексную противоречивую гипотезу H \ a> ao. Действуйте так же, как в §55, различая две простые гипотезы. Критерий x> Ci = оо + асас / / / будет иметь важные уровни для простой гипотезы a> a0. На следующем графике показана степенная функция этого критерия.
Рисунок 14 Следовательно, исходя из критерия x> Ci, только гипотеза H0 может быть отклонена с небольшой ошибкой. Людмила Фирмаль
В случае x> C \ нет основательной причины утверждать, основываясь только на выборке (1), что a = a0 вместо a> a0. Таким образом, если x> C, {sample (I) согласуется с гипотезой H0, и если эта гипотеза имеет обоснование, не зависящее от образца (1), выборка в этом случае подтверждает это.
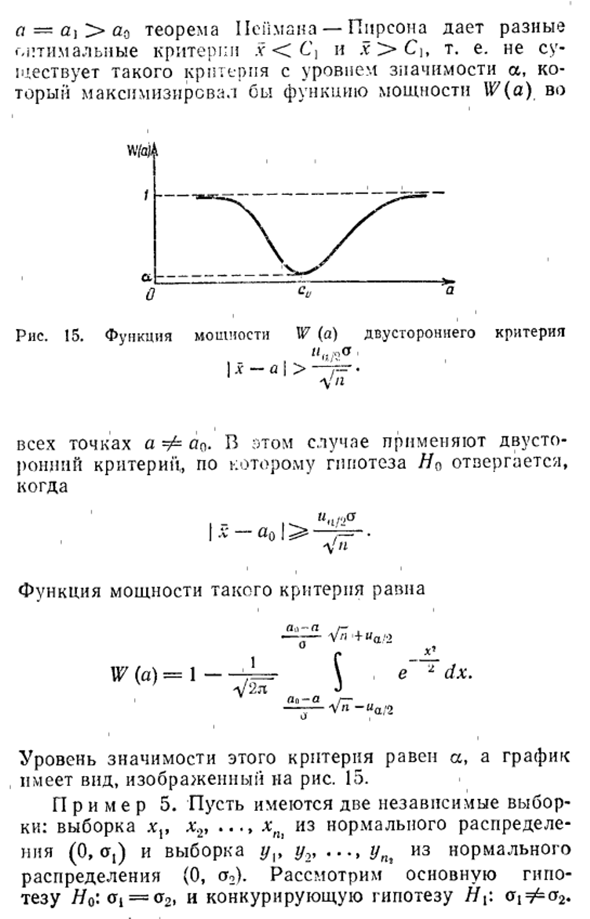
Пример 4. Сохранение гипотезы H0 одинаковой, противоречивые гипотезы с обеих сторон // //. : A F ao. В этом случае значения a = a \ Up + aa-p ^ * yn степенная функция W (a) Будет больше всего с мостом a = Oj> • G0, теорема Неймана-Пирсона дает различные оптимальные критерии x С. То есть не существует критерия максимизации экспоненциальной функции W (a) на уровне значимости a.
Рисунок 15. Степенная функция W (a) двусторонний критерий \ xa > — 7 = р. Ий Все точки Φa0. В этом случае используется двусторонний критерий, но гипотеза Но отклоняется соответственно И.В- «О Ж * Степенная функция такого критерия К —L / — —5— V / i + ia / 2 Нет (а) = 1-tL = t \ e ~ dx. U2ya J jav-a r —3— Vn- “a / 2
- Уровень значимости этого критерия равен a, и график принимает вид, показанный на рисунке 3. 15. Пример 5. Предположим, у вас есть два независимых образца. Выборка xv xv xn% из нормального распределения (0, aj) и выборка * / ,, Y2> ••• Yn из нормального распределения (0, a2).
Основная гипотеза H0: Гипотеза H {: o {Φa2, которая конкурирует с a1 = a2. статистика «Я 1 В> F = -T1-0 » 1 В ««> 112 / ‘ Гипотеза имеет распределение F0 ^ Фишера. Критерии могут быть созданы на основе статистики (16). Пусть Fy — квантиль / ^ статистики (10) P {F> Fy \ H0} = y. Примите гипотезу I0. F | -a / 2 ^ F Faf>.
Уровень значимости этого критерия составляет. Людмила Фирмаль
Смотрите также:
Решение задач по теории вероятностей
| Оптимальный критерий Неймана-Пирсона | Непараметрические критерии |
| Оптимальные критерии для проверки гипотез о параметрах нормального и биномиального распределений | Условные законы распределения |
Если вам потребуется помощь по теории вероятности вы всегда можете написать мне в whatsapp.

