Оглавление:









Условное распределение точек пуассоновского процесса
- Следующее утверждение о пуассоновском процессе и Независимая экспоненциальная ель. с. главный Теоретические и прикладные ценности: « Лемма 2. Сделайте Xt, X2, … экспоненциально независимыми Поставляется с параметром А. эл. с. Sn = Xi + … + Xn, n = = 1. 2. …, Λ ‘ 0, 0 х <0; (II) ели условную плотность сустава. с. Под Si Sn Предоставленное питание. с. Sn + я равны fs, .., sn \ sM (yi Y „\ Yn + ) = -? -, 0 0, A6) есть n! Это равно бн. Другими словами, плотность суставов Итак, плотность количества? /)), Следовательно, результаты (II) и (IV) Условная плотность fa sn \ sn * i И fa ^ «(О, *] Соответствие плотности статистики заказов по форме
Распределение по [0, Sn + ] и [0, *]. | Доказательство. (I) Уравнения (9) и А1) и Получить и получить Sn <* из события 5n + 1 ^ x Это ^ e-4 A7) Последовательно используйте A7), чтобы получить η = 1,2, … Заметим, что для ф есть S \ = XU. Я ел. с. Sn: A8) А8) дифференцируется по х и сокращается,
Плотность распределения ели. с. 5 „: (II) 0 Выберите 0, Y \ + b> y2, yk + & <Узин + b> yn + i. Далее, учитывая лемму 1, Мы получаем F (yi 0, я + я, я = л, …, я-1, Людмила Фирмаль
В B2) Интеграция выполняется на (n + 1) размерном наборе B ”= {{yi ¦ ¦-, yn + ) ¦ Xi 0 с неизвестным? .. Если true, значение n ~ L B4) Это можно рассмотреть в соответствии с замечаниями к лемме 2. Как порядковая статистика равных независимых выборок Равномерно с распределением [0,1]. Поэтому возможность Применяйте разные методы для проверки согласованности Дано (известное) теоретическое наблюдение ф. р 4. Примеры. Следующие данные о количестве рейсов Время непрерывного сбоя установки кондиционера Кондиционер самолета Боинг 720 [4]: 42 23 246 71 261 21 и 37 12 14 7 20 11 120 5 16 14 12 90 62 120 1 47 11 16 225 52 71 14 95
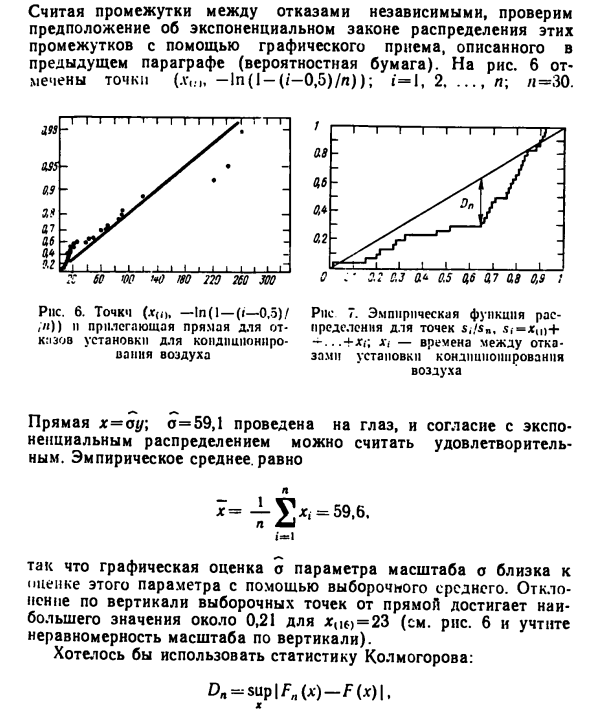
Проверка с учетом интервала между независимыми сбоями Предположения для этих экспоненциальных законов Интервал с использованием графической техники, описанной в Предыдущий абзац (вероятностный документ). Рисунок 6 Точки помечены (l-,. „-Ln (I — (/ — 0,5) / n)); i = l, 2, …, n; / j = 30. в качестве ZSS 0.9 * Al 0.6 0 » о 1 1 1 1 — W ! 1 1 11111 ‘v:’ ¦ ¦- ^ т • — это я я я я я | ? C 60 ’00 ‘* 0 180 220 210 0,2 0,3 а * 0,5 0,6 0,7 0,8 0,9 1 PNC. 6. Точка (lH (o, -InA- (i-0.5) / Pile 7. Эмпирическая функция ,))) А соседняя линия точки s, / Sn, s, = xu) + отрыв кизов установка кондпшюниро — … + рт. ст. «/ -Неисправность интервал-
- Установка кондиционера в Японии воздуха Линия x = ay \ o = 59.1 нарисована на глаз и совпадает с экспозицией. Экспоненциальное распределение можно считать удовлетворительным Я доволен. Эмпирическое среднее значение х = 1 = 1 Следовательно, графическая оценка масштабного параметра o Нажмите на этот параметр, используя примерное среднее. от Вертикальное отклонение точки отбора от линии достигает максимума Максимальное значение x составляет около 0,21 | | f) = 23 (см. Рисунок 6 и примечание) Вертикальные неровности). Я хочу использовать статистику Колмогорова: Оценить значимость наблюдаемого отклонения e. е. от г Теоретический ф. г Однако,
Теоретическая fp F (x / o) = l — e ~ x ° содержит неизвестные p-ara- Около метра. Критерий Колмогорова может быть применен к этой проблеме. Проблема с использованием леммы 2. Вычислить значение s, = Vx /. Где х, — Непрерывное время между отказами, / = 1, …. 30: 43 +23284371378478512574621846917 1163 1184 1226 1246 1251 1263 1383 1394 1397 1411 1482 1493 1507 1518 1534 1624 1625 1641 1693 1788 При делении на S3o = 1788 получается следующий набор значений: 5 «..- с ./s_- I-1 OQ * ¦ * (!) ~ — ^ 1 / ^ 30 «* ~ *» * * * на A * 7. 0,0128 0,1588 0,2074 0,2114 0,2785 0,2863 0,3210 0,3473 0,4731 0,5128 0,6504 0,6621 0,6856 0,6968 0,6996 0,7063 0,7734 0,7796 0,7813 0,7891 0,8288 0,8350 0,8428 0,8485 0,8579 0,9082 0,9088 0,9177 0,9468 E.F.R. 2 @, i = l, …, 29, см. Диаграмму. 7. Затем ? > „= 0.6504- = 0.2056, / 29 Dn = 1.107, 3 * (VnDn> \, \ 07) i9 I- / C (l, 107) = 0,173, То есть примерно в 17 из 100 случаев это можно было наблюдать Такое же или большее отклонение.
Смотрите также:
| Примеры графического анализа | Оценивание параметров экспоненциального распределения |
| Экспоненциальное распределение и пуассоновский процесс | Оценивание по первым г порядковым статистикам |

