Конвективный теплообмен

Оглавление:

Конвективный теплообмен

Процесс теплоотдачи .При неизотермическом движении среды процесс конвекции всегда сопровождается теплопроводностью, роль которой зависит от характера течения и свойств жидкости. Условимся в дальнейшем под жидкостью (средой) понимать не только капельную жидкость, но и газ. Процесс теплоотдачи может происходить при естественной (свободной) и вынужденной конвекции. Естественная конвекция, например, воздуха в помещении сопровождается его нагревом от радиатора отопления.

Вынужденная конвекция, например, при движении нагретой жидкости под действием разности давлений на концах трубы сопровождается ее охлаждением. Интенсивность теплоотдачи зависит от многих факторов и в частности от вида конвекции (свободная или вынужденная), режима течения жидкости (ламинарный или турбулентный), физических свойств среды (плотности р, теплопроводности X, динамической вязкости р, массовой удельной теплоемкости с, коэффициента объемного расширения о а₌ _ ( &. | /р, а также от формы и \гтЛ размеров теплоотдающей или тепловоспринимающей поверхности обтекаемого средой тела.

В общем случае вынужденная конвекция может происходить вместе с естественной (смешанная конвекция). Людмила Фирмаль

Естественная (свободная) конвекция возникает под действием неоднородного поля внешних массовых сил (сил гравитационного, инерционного, магнитного или электрического поля), приложенных к частицам жидкости внутри системы. Вынужденная конвекция возникает под действием внешних поверхностных сил, приложенных на границах системы, или под действием однородного поля массовых сил, действующих в жидкости внутри системы. Вынужденная конвекция может осуществляться также за счет запаса кинетической энергии, полученной жидкостью вне рассматриваемой системы. При обтекании твердых тел потоком вязкой несжимаемой жидкости с постоянными физическими свойствами процесс теплоотдачи описывается системой дифференциальных уравнений, включающей уравнения движения, неразрывности и энергии.

В двухмерном приближении эта система уравнений имеет вид р (dwₓ/dt) = -+ pgₓ$AT + р\⁷²н> полагалось, что зависимостью р от р можно пренебречь и входящая в уравнения плотность р = const (несжимаемая жидкость). Однако причиной естественной конвекции является изменение плот- ности в зависимости от температуры, что учтено произведением рд/’. (Это справедливо при линейном изменении плотности от температуры.) Уравнение (2.55) выражает закон сохранения энергии и является уравнением энергии. Оно может быть выведено р (dWy/dt) = — -^ + Pg>PAT+ (2.53) путем замены в уравнении теплопроводности (2.25) справедливого дчя твер- (2.54) дою тела частной производной ат St рсИТ/Л)-*?²?, (2.55) на полную dT/dt.

Такая замена произведена с целью перехода от твердого тела к движущейся среде, в которой где х и у — декартовы координаты; и w, — проекции вектора скорости на оси х и у; р — разность действительного давления движущейся жидко сти и гидростатического давления покоящейся жидкости; gₓ и gᵥ — проекции ускорения поля внешних массовых сил; ДТ=Т-Т,;//Л=| ₊ «4₊>Ъ. А_ полная производная условиях стационарных процессов — sso). При выводе уравнений движения (2.52), (2.53) и уравнения неразрывности (2.54) использованы второй закон Ньютона, закон сохранения массы и опытный закон вязкого трения.

Физический смысл уравнений движения состоит в том, что произведение массы на ускорение [р(/н/(й)] равно сумме всех сил, действующих на элемент объема, вылеченный в жидкости [сил давления grad р, подъемной силы pg0A7; равной разности архимедовой силы выталкивания и силы тяжести, и сил внутреннею трения (pV²w), вызванных вязкостью жидкости]. Можно также сказать, что эти уравнения выражают закон сохранения импульса. При выводе уравнений движения пред температура можег изменяться не только в зависимости от времени, но и вследствие перемещения элемента объ ема в пространстве.

Таким образом, левая часть уравнения (2.55) учитывает перенос теплоты путем конвекции, а правая — путем теплопроводности. Уравнения энергии для газа и жидкости несколько различаются. В простейшем случае течения несжимаемой жидкости с постоянными X, р, с и Р различие состоит в том, что в уравнении (2.55) для газа вместо теплоемкое! и с используется изобарная теплоемкость Ср. Это следует из подробного вывода уравнения (2.55) на основе первого закона термодинамики. Система уравнений (2.52)—(2.55) содержит следующие неизвестные функции: wₓ(x, у), м>»(х, у), р(х, у) и Т(х, у). В общем случае между полями скоростей и температур существует двусторонняя связь.

В частном случае, когда действием подъемной силы р#рдт можно пренебречь, поле скоростей при постоянных физических свойствах жидкости не зависит от поля температур. Аналог ично уравнению теплопроводности систему уравнений (2.52)—(2.55) следует дополнить комплексом i сомстри-ческих, физических, граничных и начать- вых условий. При решении стационарных задач начальные условия не задаются. Условия однозия’вюсти определяют форму и размеры обтекаемого средой твердого тела, физические свойства среды (1, р, с, р. Р), а также условия протекания процесса на границах.

Граничные условия обычно задаются в следующей форме: wₓ = Ну = 0, Т— при У = 0; wₓ = w, Т=ТЖ при у » сс (у -координата, нормальная к поверхности тела и отсчитываемая от его поверхности; w — скорость невозмущенного набегающего потока; Г» — температура жидкости вдали от тела; ТС₁ — температура поверхности тела). Продольная coci являющая скорости wₓ = 0, так как жидкость или газ, обтекающие гело, прилипают к его поверхности, что установлено опытным путем и справедливо для сплошной среды. Условия прилипания нарушаются только при обтекании тел потоком сильно разреженною газа; wy = 0 вследствие непроницаемости поверхности тела.

В соответствии с законами теплоотдачи Ньютона (2.6) и теплопроводности Фурье (2.1) уравнение теплообмена на границе между твердым телом и средой принимает вид 11равая часть этого уравнения выражает плотность теплового потока, переносимого путем теплопроводности через теоретически бесконечно тонкий слой жидкости, неподвижный относительно поверхности обтекаемого тела. Система уравнений (2.52)—(2.56) с заданными условиями однозначности позволяет определить неизвестный ко: м)>-фициент теплоотдачи а, а следователь но, плотность теплового потока дс₁, поступающего от тела к потоку (или в обратном направлении). При этом qc, = а— 7J.

Однако аналитическое решение системы в общем виде практически невыполнимо и может быть получено только при введении упрощающих предположений. В некоторых случаях, например, дтя ламинарных течений задача может быть решена численными методами с помощью ЭВМ. Трудности теоретического исследования явлений теплоотдачи приводят к широкому использованию полуэмпиричсских методов и экспериментальных данных. Мет оды подобия и размерности Необходимые и достаточные условия подобия физических явлений.

Понятие подобия можно использовать не только в геометрии, но и распространить на физические явления. Подобными могут быть явления, имеющие одну и ту же физическую природу. Для подобия физических явлений необходимо, чтобы поля всех физических величин, характеризующих исследуемые явления, отличались только масштабом. Рассмотрим в качесгве примера подобие процессов нестационарной теплопроводности. Из уравнения теплопроводности (2.25) с учетом геометрических, физических, граничных и начальных условий следует, что явление теплопроводности в одномерном приближении характеризуется восемью размерными величинами (Т- TJ, х, Г, /, о, X, a, (Ъ — 7J, (2.57) где Т= Т(х, t) — неизвестная функция; / — некоторый характерный размер тела.

Физическое подобие возможно только при геометрическом подобии систем: *7’ = Г/Г = Сь (2.58) Условия однозначности к системе уравнений, описывающих явление теплоотдачи, состоят из геометрических, физических, граничных и начальных условий. Физическое подобие — соответствие между физическими процессами. выражающееся в тождественности их безразмерных математических описаний. где один штрих — для модели натурного объекта (на которой предполагается экспериментально исследовать явление теплопроводности)» а .

Два штри-ха — для натурного объекта, который обычно еще только проектируется; С\ — константа подобия координат и геометрических размеров. Кроме того, для подобия рассматриваемых явлений необходимо, чтобы преобразование подобия (2.58) выполнялось для всех физических величин, характеризующих явления, т. е. aw№ Cₑ; = о’/У = С; гж/гж=77/г₁ = г/г = ст; tyr = Cₜ. (2.59) Константы подобия вычисляются для сходственных точек модели и натурного объекта, т. е. точек, координаты которых связаны между собой преобразованием (2.58) и в моменты времени, соотношение которых равно С,. При существовании подобия константы Cₕ Сд, G, Са и т. д не зависят ни от координат, ни от времени. Из изложенного следует, что для подобия физических явлений необходимо, чтобы они имели одну и ту же физическую природу, описывались одинаковыми дифференциальными уравнениями и имели подобные условия однозначности.

Однако для таких сложных явлений. как процесс теплообмена, эти условия оказываются все же недостаточными для существования подобия. Уравнения, описывающие процессы теплопроводности в модели (’) и натурном объекте О, имеют вид (2.60) (2.61) В соответствии с условиями (2.58), (2.59) уравнения (2.61) можно преобразовать: с, гг ггт г,7Гг’ = с-с? с. с. иг»-г^-С^Х’(да. (2.62) Одна и та же неизвестная функция 7 ’(х, г) может быть найдена из решения уравнений как (2.60), так и (2.62). Однако это возможно только в том случае, когда уравнения (2.62) и (2.60) тождественно совпадают. Отсюда очевидна взаимосвязь констант подобия, которая в рассматриваемом случае выражашея следующим образом: Ст/С, = CₐCₓ!Cj\ СаСт = (\C-JCi. Возвращаясь теперь к размерным переменным с помощью соотношений (2 58), (2.59), получим аТ/Г² = ГГ/Г², оТД’ = аТД».

Следовательно, безразмерные комплексы Bi — at/k и Ео = (Л/1², критерии подобия для подобных явлений должны сохранять одно и то же значение. Критерии подобия с физической точки зрения выражают соотношения между различными физическими эффектами, Константы подобия — отношения однородных физических величин в сходственных точках модели и натурного объекта. Критерии подобия — безразмерные числа, составленные из размерных физических величин, определяющих рассматриваемые физические явления. характеризующими данное явление.

Например, критерий Био можно рассматривав как отношение термического сопротивления стенки (/Д) к термическому сопротивлению теплоотдачи (1/ос), в то время как критерий Фурье рассматривается как отношение времени протекания процесса (Г) ко времени изменения температурного поля в теле В связи с этим условия (2.63) имеют следующий физический смысл: для подобия явлений необходимо, чтобы соотношения между эффектами, cyineci венными для развития процесса, были одинаковы. Чтобы использовать теорию подобия, необходимо иметь математическое описание явления.

Критерии подобия можно получить из дифференциальных уравнений описывающих явление. Практически важно, что критерии подобия, полученные из исходных дифференциальных уравнений, описывающих явление, и соотношений, представляющих результаты их решения, одни и те же. Теория подобия. Основные теоремы теории подобия можно сформулировать следующим образом. 1. У подобных явлений критерии подобия равны. Определяющими критериями подобия в рассмотренном примере являются критерии Bi и Fo, а также безразмерная координата х/1.

Определяемый безразмерный комплекс для процесса теплопроводности может быть представлен в виде отношения 0 = [Т(х, 0 — 7,1X7. — 7J, где 7(х, г) — определяемая функция. 2. Связь между определяемыми и определяющими безразмерными комплексами может быть представлена в виде некоторой функции от критериев подобия. Кри1 ериальное уравнение подобия выражается в виде 0 = G(Bi, Fo, х//). (2.64) По результатам обработки опытных данных, полученных на модели, можно определить конкретный вид функции (2.64) и таким образом обобщить полученные результаты, распространив их на вое подобные между собой явления.

Полученную зависимость затем можно использовать для расчета распределения температур в натурном объекте. Она б. удст справедлива в том диапазоне изменения определяющих критериев подобия, который был исследован в опытах на модели. 3. Необходимые и достаточные условия подобия физических явлений состоят в подобии условий однозначности и равенстве одноименных определяющих критериев. Значение теории подобия особенно велико для изучения таких явлений, как теплообмен, поскольку исследование этого процесса основано на экспериментальных данных.

Согласно теории подобия в опытах должны измеряться те величины, которые входят в состав критериев подобия. Критерии подобия могут быть выведены как из дифференциальных уравнений, описывающих данное явление, так и из размерных величин, характеризующих это явление, если точно известен их полный перечень. Следует отмет ить, что любые степеннее комбинации известных критериев Определяющие критерии подобия — числа подобия, составленные из величин, заданных при математическом описании процесса. Определяемые безразмерные комплексы — числа подобия, содержащие определяемую величину.

Критериальные уравнения подобия — функциональные зависимости между критериям^ подобия, характеризующими явление. также являются правильно составленными критериями подобия. Тем не менее число их для каждого конкретного случая вполне определенное и соответствует следующему общему принципу теории размерности: функция, связывающая т размерных величин, содержащих п основных единиц измерения, приводится к зависимости между т — п безразмерными комплексами.

В рассмотренном выше примере процесса теплопроводности в соответствии с перечнем величин (2.57) т = 8 при числе основных единиц измерения п = 4 (длина, время, масса и температура), поэтому зависимость (2.64) должна содержать четыре критерия подобия (т — п = 4). Критерии подобия процессов теплоотдачи. Уравнения (2.52)—(2.56) позволяют получить безразмерные комплексы, характеризующие процесс теплоотдачи. Остановимся теперь на упомянут ом выше более общем методе, который применим и в том случае, когда математического описания явления еще не существует.

Из опыта известно, что интенсивность теплоотдачи при обтекании твердого тела потоком однофазной химически однородной изотропной несжимаемой жидкости с постоянными физическими свойствами (при отсутствии переноса теплоты излучением) зависит от следующих восьми размерных величин, входящих в уравнения (2.52)—(2.56), описывающие процесс теплоотдачи при условии пренебрежения работой сил внутреннего трения, переходящей в теплоту: характерного размера I тела, м [£]; скорости w потока, омывающего тело, м/с [LT⁻¹]; плотности р жидкости (или газа), кг/м³ динамической вязкости ц, Па-с [L-’MT-¹]; теплопроводности X, Вт/(м • К) [ШТ» ³6-’]; удельной теплоемкости с, Дж/(кг-К) [/?Т-²6-’]; подъемной силы, отнесенной к единице массы g(iAT, м/с² [LT⁻²]; коэффициента теплоотдачи а, вт/(м²ю [Ш’-’е-¹]. За основные (первичные) величины здесь приняты: длина £, масса М, время Т и температура 0.

Безразмерные комплексы процесса теплоотдачи должны быть представлены произведением степеней основных размерных величин, существенных для процесса, /ew, pup).»’cx(gpAD> a (s, t, м, v, iv, х, у и z — неизвестные показатели степени). Если в приведенном выражении заменить каждую величину соответствующей ей размерностью, то для размерности самой переменной получим LS[£T-¹],[ML-^[ML’¹T-I]₽ х х [MLT’³e».][L²T-²0″.]x[LT-²]> х х [МГ³^®-¹}’ = £U»-3«->+h^2xO) х у j—(» + r+3w + 2x + X 0-(w+x+x) Условием безразмерное™ выражения в целом является равенство нулю суммы показателей степени при каждой размерности.

Для определения восьми показателей степени необходимо составить уравнения, число которых должно быть равно числу основных единиц измерения: для длины s + t — Зи — v + w 4- 2х + у = 0; для времени f + v + 3w + 2x + 2у + 3z = 0; (2.65) для массы u + v + iv + z = 0; для температуры w + х + z = 0. Число показателей степени, для которых значения могут быть выбраны произвольно, равно, (8-4). Пусть, например, это х, у, z и v. Тогда из уравнений (2.65) $»x + y + z-i>; t = х-— 2у — в; и = х — г; w = — (х + z), и общее выражение для безразмерных переменных примет вид x (gpAiy or’.

С учетом свободы выбора x, у, z и v можно получить четыре следующих критерия подобия: при z = 1, х — у = v = 0 число Пус-ссльта Nu = а/Д; (2.66) при v = — 1, х = у = г =0 критерий Рейнольдса Re = ир//р = h7/v; (2.67) при х = 1, v = 1, у = z — 0 критерий Прандтля Рг = цсД = v/a; (2.68) при у = 1, v — —2, х = z = 0 критерий Грасгофа Gr = (gpAT)/³p²p~² = g/³0ATv⁻², (2.69) где v — кинематическая вязкость (v = = р/р)- При выборе любых других конечных значений х, у, z и г определяются безразмерные комплексы, представляющие лишь различные степенные комбинации из тех, которые уже получены.

Число критериев подобия рассматриваемого процесса (т — л) ■- 4, что соответствует сформулированному выше общему принципу теории размерности. Наряду с полученными критериями подобия в теории подобия используются также следующие безразмерные комплексы. Число Стантона St = Nu/(Re Рг) = a/(cpw) (2.70) характеризует соотношение между изменением температуры жидкости по длине обтекаемого тела и температурным напором. Критерий Пекле Pc = Re Рг = к//д. (2.71) Так как Ре » рсн, Л7’/(ХЛ7′//), этот критерий характеризует отношение плотности теплового потока, переносимого движущейся жидкостью, к плотности «оплового потока, переносимого теплопроводностью.

Критерий Редея Ra = Gr Рг = #/³0A77(va). (2.72) Конкретная форма безразмерных комплексов в каждом случае выбирается с учетом физического смысла. Функциональная зависимость между безразмерными переменными может быть представлена в виде Nᵤ as Nu (Re, Pr, Gr). (2.73) Число Nu содержит неизвестную функцию — коэффициент теплоотдачи а и является определяемым безразмерным комплексом. Поскольку число Nu опре-деляется выражением аАТ/[(ХД)АТ]. его можно рассматривать как отношение плотности теплового потока, переносимого путем конвекции, к плотности теплового потока, проходящего через плоский неподвижный слой жидкости толщиной / в условиях теплопроводности [см. уравнения (2.6), (2.16), (2.56)].

От определяющих критериев подобия Re, Gr и Рг кроме числа Nu зависят безразмерная скорость, температура и давление [см. уравнения (2.52) —(2.56)]. Эти определяемые безразмерные комплексы появляются при анализе размерности в тех случаях, когда в число исходных размерных величин кроме а входят неизвестные функции (скорость, температура и перепад давлений). Поскольку каждый из критериев соответствует определенному дифференциальному уравнению, физический смысл критериев подобия связан с физической сущностью уравнений (2.52)—(2.56). Например, критерий Re характеризует отношение сил инерции, действующих в жидкости (pw²//), к силам внутреннего трения (pw//²). Это следует из уравнений (2.52), (2.53), так как степенные комплексы, указанные в скобках, характеризуют эти силы.

Критерий Gr можно рассматривать как безразмерный комплекс, пропорциональный подъемной силе р#0А7^ силе инерции и обратно пропорциональный квадрату сил внутреннего трения, вызванных вязко- Гр^рЛТ(ри^/П»| — L 0W—Г Критерий Рг — безразмерный физический параметр, зависящий от ц, X и с и характеризующий связь скорое того и температурного поля в жидкости [см. уравнение (2.55)]. Для газов 0,6 Рг 1; для капельных жидкостей (вода, различные органические и неорганические жидкости) I Рг 200; для очень вязких жидкостей значение Рг достигает нескольких тысяч.

Для жидкометал-лических теплоносителей 0,005 Рг 0,05. Уравнение подобия (2.73) используется в том случае, когда в процессе теплоотдачи вынужденное движение среды сопровождается свободным (смешанная конвекция). Если роль свободного движения в процессе переноса теплоты мала по сравнению с вынужденным, то выполняется условие Gr/Re² 1, при котором критерий Gr из уравнения (2.73) можно исключить. При свободной конвекции из уравнения (2.73) исключается критерий Re. В таких задачах скорость неизвестна, и безразмерный комплекс Re является определяемым.

Критерии подобия процессов теплоотдачи были выведены в предположении, ч ю физические свойства среды постоянны. В действительности величины X, ц, с и р зависят от температуры и давления, и их изменение влияет на интенсивность теплоотдачи. При переменных свойствах жидкости система уравнений, описывающих процессы теплоотдачи, (2.52)-(2.56) становится более сложной. Влияние на процесс теплоотдачи изменения физических свойств жидкости при изменении ее температуры может быть учтено введением в критериальное уравнение безразмерных отношений (рсг/ржХ Р’ст/Хж), (Рсг/Рж), (Сет/сД (2.74).

Это влияние становится особенно существенным при больших разностях | Тс — Тж |, а также в околокритической области состояния вещества. Учет влияния всех аргументов достаточно сложен, поэтому при расчете процесса теплоотдачи, например капельной жидкости, принимается во внимание только наиболее сильно изменяющаяся с температурой динамическая вязкость. При построении критериальных уравнений подобия величины щ X, с и р относят к некоторой определяющей температуре, которой может быть например. среднемассовая температура жидкости Тж при теплоотдаче в трубах; температура потока, обтекающего тело, температура поверхности тела (ТС₁) или температура, значение которой зависит от Тж, (Тш) И Тст.

Входящие в критерии подобия характерные значения длины /, скорости w и разности температур АТ выбираются с учетом физического смысла и конкретных условий теплоотдачи. Так, при расчете теплоотдачи в трубах и каналах за характерный размер принимается внутренний диаметр трубы или эквивалентный диаметр канала (если сечение канала некруглое) d₃ = 4 Л/77, где А — площадь поперечного сечения канала; П — периметр сечения. Характерной скоростью является ос-редненное по сечению канала значение w. При внешнем обтекании тел характерным размером обычно считается координата, направленная вдоль контура обтекаемого тела, а характерной скоростью — скорость невозмущенного набегающего потока.

Аналогичным образом выбирается характерная разность температур (АТ), входящая в критерии Gr (2.69) и Ra (2.72). Например, в зависимости от конкретных условий величина АТ может быть равна следующим разностям температур: тела и среды; стенок щели, в которой исследуется теплообмен; во входном и расчетном сечениях грубы (канала). w/wₑ Рис. 2.4. Изменение относите. и>иой скорое гк и’/и’о в зависимое ih от r; R на иача львом участке трубы при лаканарном режиме течения: / — А’— 0: 2 — Y = 8,3 10-⁴:3-У = 35,7-10«; 4-Х >0,62 ’Речение жидкости в трубах и каналах Ламинарный режим течения жидкости (или газа) — режим течения параллельных слоев («ламин»), которые не перемешиваются между собой. Взаимодействие слоев обусловлено вязкостью и различием скоростей.

При ламинарном течении критерий Re не достигает критического значения. При течении в трубах Re» = wp//p = 2300 — 10⁴, где iv — средняя по сечению скорость течения жидкости в трубе; d — внутренний диаметр трубы. Значение ReK зависит от условий входа в трубу, шероховатости поверхности стенок, интенсивности теплообмена, формы сечения трубы (канала), наличия внешних массовых сил, сжимаемости и некоторых других факторов. Локальные и средние характеристики течения и теплообмена при движении жидкости в трубах при Re 2300 показаны на рис. 2.4.

Из опыта известно, что при стационарном изотермном течении на достаточном удалении от входа в трубу скорость жидкости по радиусу грубы изменяется по закону параболы. При этом в каждой точке потока скорость параллельна оси х, направленной вдоль оси трубы, не зависит от координаты х и определяется формой сечения трубы. Такое течение называется гидродинамически стабилизированным. Изменение относительной скорости w/«v₀ в зависимости от r/R на начальном участке трубы при ламинарном режиме течения показано на рис. 2.4.

Профиль скорости 1 на входе в трубу может быть произвольным. На некотором начальном участке трубы, вследствие действия сил внутреннего трения, он изменяется и стремится принять форму 4, соответствующую стабилизированному течению. Известно, что на участке трубы с установившимся профилем скорости потери энерти на трение минимальные. Вследствие действия сил внутреннею трения и прилипания жидкости к стенке, на начальном участке трубы возникает пристенный пограничный слой заторможенной жидкости. Толщина этого слоя растет вниз по течению до тех пор, пока он не заполнит все сечение трубы.

При постоянных физических свойствах жидкости процесс теплообмена не оказывает влияния на течение жидкости. Если свойства жидкости изменяются, то при теплообмене имеет место взаимное влияние распределения температур и скоростей, вследствие чего параболический закон распределения скоростей нарушается. Естественная конвекция при неизо-термном т ечении также существенно сказывается на профиле скорости в зави- Л аминарный режим течения — режим движения жидкости, при котором возможны стационарные траектории ее частиц. Nu, Nu bd Рис. 2.5.

Изменение местного числа Nu н среднею Nu в зависимости от Соразмерного 1 х — комплекса——при ГС| = const Ре d симости от направления теплового потока (охлаждение или нагревание), ориентации трубы в пространстве и значения безразмерного комплекса Gr/Re². В связи с указанными особенностями лечения всю обогреваемую (или охлаждаемую) трубу можно разбить на два учасчка. Термический начальный участок характеризуется изменением профиля скорости, ростом толщины пограничного слоя и уменьшением по длине местного и среднего чисел Нусссльта.

Изменение местного числа Nu и среднего Nu в зависимости от безразмерно-¹ х го комплекса ре j при /С| = const показано на рис. 2.5. Изменение профиля температуры по длине трубы на этом участке происходит так, что (dT/drfa по течению падает быстрее, чем уменьшается температурный напор, в связи с чем [согласно уравнению (2.56)] коэффициент а уменьшается. Участок стабилизированного теплообмена имеет определенную закономерность распределения температуры по радиусу, не изменяющуюся по длине (хотя абсолютные значения температуры изменяются), и постоянное число Nu.

Относительная длина термического начального участка lHₜ/d = О, О55Ре, (2.75) где Im — отсчитываемая от входа в трубу длина участка; Ре=вт//а; «^=Х/(ср). Для среднего по длине числа Нус-сельта величина l^/d значительно больше и равна 1,365Ре (см. рис. 2.4). Таким образом, длина 1ЦХ зависит от диаметра d трубы, скорости w и физических свойств жидкости (X, с, р). При наличии естественной конвекции на величину /мг существенно влияет также ориентация трубы в пространстве. Местный (локальный) коэффициент теплоотдачи в круглой трубе может быть определен по полуэмпирической формуле Nu = 1,03 (Ре d/x)¹’³ (Рж/М⁰, ¹ (2.76) .

Эта формула справедлива для капельных жидкостей при д/(Ре d) 0,01 и 0,07 Рст/Цж 1500. Физические свойства жидкости, входящие в критерии Nu == ad/X. (2.66) и Ре = wd/a (2.71). отнесены к температуре 0,5 (ТС₁ + 7), а а = = — Т) (Т — средняя массовая температура жидкости в данном сечении). Термический начальный участок — участок трубы, на котором поле температуры зависит от условий на входе в трубу. У част ок стабилизированного теплообмена — участок трубы, на котором поле температуры практически не зависит от распределения температуры в начальном сечении обогреваемого участка.

Составив и проинтегрировав уравнение теплового баланса для круглой грубы, получим выражение, необходимое для определения Т, в виде (7 — ТСТ)ДТО — Тст) = 1 — 6,46 (х/Ре J)²/³, (2.77) где х — продольная координата, отсчитываемая от входа в трубу; То — температура жидкости на входе в трубу. После интегрирования выражения (2.76) по х можно получить критериальное уравнение для среднего (по длине трубы) коэффициента теплоотдачи Nu = l,55(Ped//)IZ³K/pCT)⁰¹\ (2.78) где Nu = otJ/л; а = qCJ/(T» — Т); qcₜ -средняя по поверхности трубы плотность теплового потока; / — длина расчетного участка.

Физические свойства жидкости и цж отнесены к~ определяющей температуре 7″-0,5(Д7Ъ где (ДТ)л = (ДТ — ДГ)/ /1п(ДТ’/ДТ’) — средний логарифмический температурный напор; ДТ’ и ДТ» — температурный напор | Тег — Т| во входном и конечном сечениях расчетного участка трубы. Формула (2.78) применима при x/(Ped) 0,05, т. е. для длин труб, обычно применяемых в теплообменных аппаратах. Формулы (2.76) и (2.78) используются при Ra = 1Тт — — То l/(v») 8 • 10⁵, т. е. когда влияние свободной конвекции на вынужденное течение несущественно.

Расчет среднего коэффициента теплоотдачи в кру1 лых вертикальных трубах при смешанной конвекции можно выполнить по формуле, которая получена для условий совпадения направлений вынужденной и свободной конвекции: Nucᵣ = 0.35 (Ре d//)⁰, ³ (Ra d//)⁰’¹⁸. (2.79) Величины, входящие в формулу (2.79), определяются соотношениями Nucₗ = = ztd/K,; ОС = (fc-r (Т» — То); Ре = wd/a; Ra = | T» — T, | (va); T, = 0,5 (Tₒ + + ТД Параметры, характеризующие физические свойства жидкости и входящие в Ре и Ra, отнесены к Тж, причем Т, — средняя массовая температура жидкости в конечном сечении расчетного участка трубы. Формула (2.79) справедлива при 20 l/d 130; Ped/I 1100; 8 • 10s Ra 4 • 10я и Re Re,. В рассматриваемых условиях Re» зависит от Ra = Gr Рг.

По опытным данным число Re, = 5,283 • 10″ ⁴ Ra 4- 2500 при 0 Ra 5,3 ■ 10⁶ и Re, = 1,848 • 10″ ⁴ Ra + 4320 при 5,3-10⁶ Ra 1,6 IO⁷. В случае противоположного направления вынужденной и свободной конвекции в вертикальных трубах происходит интенсивное перемешивание жидко сти, и уже при Re > 250 течение подчиняется закономерностям турбулентного движения. Следует отметить, что интенсивность смешанной конвекции в горизонтальных трубах выше, чем в вертикальных (при совпадении направлений вынужденной и свободной конвекции). Это объясняется наложением по перечной циркуляции на движение жидкости вдоль оси.

При ламинарном течении введенная в поток окрашенная жидкость движется в трубе в виде резко очерченной струйки. При переходе к турбулентному режиму струйка расплывается, равно мерно окрашивая всю жидкость. Турбулентный режим кроме основного осевою течения жидкости характеризуется поперечным движением, приводящим к обмену импульсами в поперечном направлении при сохранении каждой частицей своего импульса в продольном направлении. Благодаря интенсивному перемешиванию жидкости при турбулентном течении, профиль скорости становится более равномерным .

Турбулентный режим — режим движения жидкости с хаотически изменяющимися во времени траекториями частиц, при котором в потоке возникают нерегулярные пульсации скорости, давления и температуры, неравномерно распределенные в потоке. 1 + Рис. 2.6. Изменение относи тельной скорости и’/н|паА в зависимости от т, К при турбулентном 1еч€ини в гр) бе: / — гидравлически гладкая поверхность; 2 — Rfkₛ = 507; 3 — R/k> = 126: 4 — Rjkₓ = 30,6 {кх — высота неровностей) (рис. 2.6), чем при ламинарном (рис. 2.4). Скорость, давление и температура в каждой точке потока беспорядочно изменяются (пульсируют) во времени с высокой частотой, поэтому зги параметры обычно осредняются по времени. При значениях Re, близких к критическим, течение носит перемежающийся характер и переходит через неравномерные промежутки времени из одной формы в другую.

Интенсивность теплоотдачи при турбулентном течении (при прочих равных условиях) всегда выше, чем при ламинарном. Если при ламинарном течении формулы для расчета коэффициентов теплоотдачи в некоторых случаях могут быть получены на основе приближенного решения системы уравнений (2.52) (2.56), то при турбулентном необходимо дополнительно использовать экспериментальные данные. Так, для расчета теплоотдачи при турбулентном течении двухатомного газа в трубах может быть рекомендована следующая критериальная зависимость, которая справедлива при 7 • 10³ Re 2 • I0⁵; 1,2 x/d 144 и 1 Тст/Тж 7,5: Nu =0.024Rc⁰HPr°’⁴^Z ’[ W1 ’ (2.80).

Для капельных жидкостей при 2300 Re 15-10 Nu = 0,116 [1 + (d/0²’³] (Re²/³ — — 125) Рг¹/³ (Рж/Mci)⁰’¹⁴ (2.81) Это уравнение получено на основе обработки большого количества экспериментальных данных методами теории подобия. Все физические параметры в формулах (2.80) и (2.81) отнесены к средней массовой температуре среды. С помощью температурного фактора Тсг/Тж в зависимости (2.80) и отношения (Рж/Рст) в формуле (2.81) приближенно учтено влияние изменения физических свойств газа и жидкости с температурой на интенсивность теплоотдачи. Уравнения (2.80), (2.81) предназначены для расчета теплоотдачи при нагревании газов и жидкостей.

Они справедливы для среднего коэффициента теплоотдачи, и в них учитывается также влияние длины термического начального участка. Поперечное обтекание одиночной круглой трубы и пучка труб При обтекании тел с тупой кормовой частью тонкий пристеночный слой жидкости, заторможенной вследствие трения (пограничный слой), образуется только на передней половине поверхности тела. Для частиц жидкости, находящихся вне пограничного слоя, на пути от точки D к точке Е (рис. 2.7, а) потенциальная энергия давления преобразуется в кинетическую.

На пути от точки Е к точке F, наоборот, кинетическая энергия опять преобразуется в энергию давления, причем в точку F частица приходит со скоростью, равной скорости в точке D. В непосредственной близости к поверхности цилиндра на пути потока от б) Рис. 2.7. Вснникнонеяис HoiHpaoiui о к-чснин к обра зоншие нмхреи при поперечным обтекании крукшсп о цилиндра: а —схема отрыва пограничного слоя и кривая изменения статического давления р вдоль контура тела; 7 — мгновенная фотография течения точки D к точке Е часть кинетической энергии расходуется на внутреннее гре-ние. вызванное вязкостью.

В результате, кинетической энергии потока оказывается недостаточно, чтобы преодолеть повышение давления на пути от точки Е к точке F, частицы жидкости, не достигая точки F, под действием распределения давления во внешнем течении начинают двигаться против потока, и пограничный слой отрывается от тела. Обратное течение обусловливает образование правильной последовательности вихрей за телом, вращающихся попеременно то вправо, то влево (рис. 2.7, б). При Re»W/v>10³ [см. выражение (2.67)] частота п отрыва вихрей в секунду подчиняется закономерности nd/w = = 0,21 (w — скорость набегающего потока и d — диаметр цилиндра). Регулярные вихревые дорожки существуют при 60 Re 5000.

При этом течение за цилиндром остается ламинарным. При Re > 5000 течение тановится турбулентным. Положение точки отрыва зависит от режима течения в пограничном слое. При Re > ReK = wrf/v st 5 I0⁵ т очка отрыва несколько смещается вниз по течению, это приводит к заметному снижению сопротивления при обтекании цилиндра. По мере роста толщины пограничного слоя местный коэффициент теплоотдачи на передней половине поверхности цилиндра уменьшается, а на задней половине (в вихревой зоне) увеличивается. Характер распределения а по поверхности цилиндра в значительной мере зависит от числа Re.

На рис. 2.8 показано изменение местного числа Nu по поверхности цилиндра в полярной системе координат. На основании опытных данных средний коэффициент теплоотдачи на поверхности поперечно обтекаемого кругового цилиндра (трубы) может быть вычислен по формулам: при 5 Re* 10³ Nu* = 0,5Re, ⁵Pr^®’³⁸(Prw/Prcᵣ)⁰-²⁵; при 10³ Re = 2 −10⁵ Nu* = 0,25Re-⁶Pr‘³⁸ (Pr/Prₜₗ)⁰-²⁵; (2.82) при 2 • I0⁵ Re 2 • К)⁶ Nu* = 0,023Re^®⁸Pr£-³⁷(Pr/PrCT)°’²⁵. В качестве характерных величин выбраны диаметр цилиндра и скорость Рис. 2.8. И1м»немне местного числа Nu по пинсрхшк-ш цилиндра (в полярной снсюме координат): I — Rc = 0 3.98 ■ КН; 2 — Re ■= 10.1 10⁴; 3 -Re — 17 • КН; 4 — Re = 25.8 • 10⁴; 5 — Re = 42.6 I0⁴ набегающего потока, а определяющей температурой является 7.

Значение РгС₁ определяется при средней температуре поверхности цилиндра. Отношение критериев Прандтля учитывает изменение физических свойств теплоносителя в зависимости от температуры. На интенсивность теплоотдачи кроме критериев Re и Рг существенное влияние оказывает начальная турбулентность набегающего потока. Так, повышение среднего квадратичного значения осред-ненных во времени пульсационных составляющих скорост и при турбулентном течении на 2,5% приводит к увеличению числа Nu на 80%. Количественные данные об этом влиянии получены экспериментальным путем.

В теплообменных устройствах приходится рассчитывать теплоотдачу пучка груб, характер обтекания которых еще более сложен и зависит ог компоновки пучка. Существенное значение здесь имеет также относительный поперечный (Si/J) и продольный (S₂/f/) шаги труб. Различают коридорное и шахматное б) Рис. 2.9. Схемы расположения груб в пучках: а — коридорное; б — шахматное расположение труб в пучке (рис. 2.9). Условия обтекания труб первого ряда в обоих случаях близки к условиям обтекания одиночной трубы.

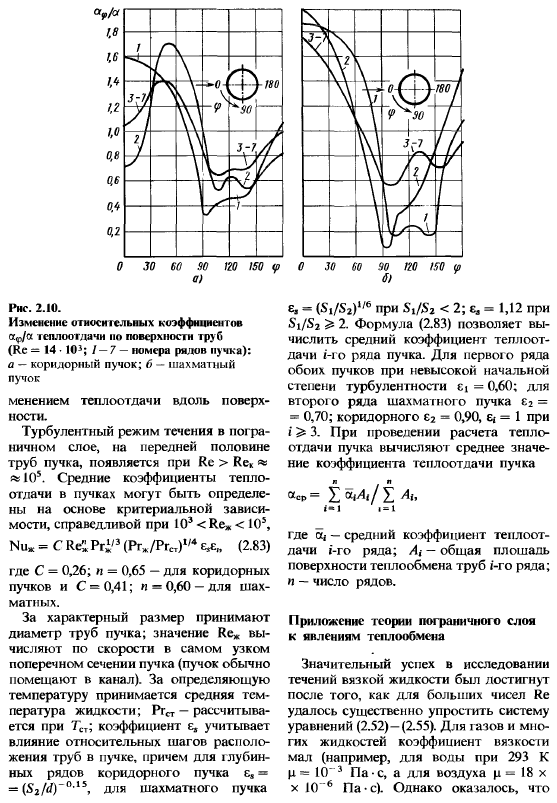
В коридорных пучках каждая последующая труба находится в вихревой зоне, образованной предыдущей трубой Вследствие различных условий обтекания труб коридорного и шахматного пучков характер распределения мест ных коэффициентов теплоотдачи по поверхности труб в этих двух случаях неодинаков. Изменение относительных значений коэффициентов теплеют дачи о^/а по поверхности труб при Re = 14 1()л можно оценить по данным рис. 2.10. На поверхности труб второго и последующих рядов коридорных пучков максимум коэффициента теплоотдачи находится не в передней критической точке, соответствующей р = 0, а смешен вниз по течению и соответствует месту срыва струй с труб предыдущего ряда.

В шахматных пучках труб всех рядов максимум коэффициента теплоотдачи так же, как и для одиночного цилиндра, находится в передней критической точке. Уровень средней теплоотдачи по поверх-ности труб выше у шахматного пучка. Это объясняется лучшим перемешиванием жидкости в этом пучке. При проектировании теплообменных устройств учитывается гидравлическое сопротивление пучка, ею засоряемость, а также величина термических напряжений материала, связанных с резким из- а) 1нс. 2.10. Изменение относи кльных коэффициентов а^а теплоотдачи по поверхности труб (Re = 14 10J; 1 — 7 — номера рядов пучка): а — коридорный пучок; 6 — шахматный пучок менением теплоотдачи вдоль поверхности.

Турбулентный режим течения в пограничном слое, на передней половине труб пучка, появляется при Re > ReK » » К)⁵. Средние коэффициенты теплоотдачи в пучках могут быть определены на основе критериальной зависимости, справедливой при 10³ Re* 10⁵, Nu» = С Re Pri’³ (Pr/PrCT)¹’⁴ (2.83) где С = 0,26; п = 0,65 — для коридорных пучков и С = 0,41; п = 0,60 — для шахматных. За характерный размер принимают диаметр труб пучка; значение Re* вычисляют по скорости в самом узком поперечном сечении пучка (пучок обычно помещают в канал).

За определяющую температуру принимается средняя температура жидкости; Ргст — рассчитывается при Тст; коэффициент £j учитывает влияние относительных шагов расположения труб в пучке, причем для i дубинных рядов коридорного пучка е, = = (S₂/j)~⁰¹⁵, для шахматного пучка е, = (S’i/S₂)¹/⁶ при S1/S2 2; €л = 1,12 при Si/S₂ > 2. Формула (2.83) позволяет вычислить средний коэффициент теплоотдачи i-ro ряда пучка. Для первого ряда обоих пучков при невысокой начальной степени турбулентности ci = 0,60; для второго ряда шахматного пучка £₂ = » 0,70; коридорного е₂ = 0,90, = 1 при i 3. При проведении расчета теплоотдачи пучка вычисляют среднее значение коэффициента теплоотдачи пучка аср= f ^Ai/Y Аь i»l i=l где — средний коэффициент теплоотдачи i-ro ряда; А, — общая площадь поверхности теплообмена труб i-ro ряда; п — число рядов.

Приложение теории пограничного слоя к явлениям теплообмена Значительный успех в исследовании течений вязкой жидкости был достигнут после того, как для больших чисел Re удалось существенно упростить систему уравнений (2.52)—(2.55). Для газов и многих жидкостей коэффициент вязкосзи мал (например, для воды при 293 К ц = 10″ ³ Па с, а для воздуха ц = 18 х х 10 ⁶ Па • с). Однако оказалось, что в непосредственной близости от поверхности обтекаемого тела вязкость жидкости (газа) имеет существенное значение, так как реальная (вязкая) жидкость не скользит по поверхности твердого тела, а прилипает к ней.

Переход от нулевой скорости на поверхности тела к скорости внешнего течения совершается в очень тонком динамическом пограничном слое. В связи с этим все поле течения можно условно разделить на тонкий слой жидкости (или газа) у поверхности тела (пограничный слой) и область внешнего течения. Согласно элементарному закону тре ния касательное напряжение т между двумя слоями движущейся жидкости пропорционального градиенту скорости 8у ’ т. е. скорости деформации т = ц (2.84) где w, — продольная составляющая ско рости, множителем пропорциональности является динамическая вязкость ц; у — нормаль к поверхности скольжения (поперечная координата).

Поскольку в области пограничного слоя значения. * велики, касательные напряжения трения и, следовательно, силы внутреннего трения в этой об ласти, несмотря на то, что у мало, могут достигать таких больших значений, что они становятся соизмеримыми с силами инерции, действующими в жидкости. В области внешнего течения * * О, поэтому вне пограничного слоя действие вязкости не проявляется, течение происходит без трения. В этой области преобладают силы инерции, и жидкость можно считать невязкой.

С учетом указанных выше особенностей при достаточно больших числах Re скоростное и температурное поле в пограничном слое может быть описано системой уравнений более простой, чем система (2.52)—(2.55). Результаты измерений показывают, что относительная толщина пограничного слоя 8// уменьшается с увеличением скорости потока, протяженности обтекаемой поверхности и уменьшением вязкости жидкости. Поэтому при больших Re = = WaJ/v (I — некоторый размер обтекаемого тела, характеризующий про тяжеиность обтекаемой поверхности). После приведения уравнений (2.52) — (2.55) к безразмерной форме с помощью собственных масштабов оказалось воз можным сделать следующие выводы. 1.

Разность давлений поперек пограничного слоя, которую можно было бы определить путем интегрирования уравнения. Людмила Фирмаль

Порядок членов уравнений (2.52), (2.53) и (2.55), содержащих производные г?²н» d²w дгТ и 7Р⁻’ мал ¹, ⁰ сРавнсни,° с порядком других членов соответствующих уравнений, в связи с чем при расчете течения в пограничном слое их можно исключить. 2. (2.53), имеет порядок (8//)², т. е. пренебрежимо мала. Следовательно, p(yj = const и равно статическому давлению во внешнем течении: частицы жидкости при движении вдоль оси, нормальной к поверхности тела, не обладают массой и не замедляются вследствие трения.

Таким образом, давление по длине пограничного слоя р (х) изменяется так же, как во внешнем течении. 3. Параметры течения вне пограничного слоя могу! быть определены при помощи теории невязкой жидкости или в результате эксперимента, т. е. их можно считать известными. При известном давлении р необходимость использования уравнения(2.53) полностью отпадает. 4. При течении в пограничном слое силы внутреннего трения имеют тот же порядок, что и силы инерции. Это условие выполняется, если безразмерная толщина 8// динамического пограничного слоя имеет порядок l/j/R^ = |/vAw»l), где и’л — скорость невозмушенного по тока. gxpAT + Рис. 2.11.

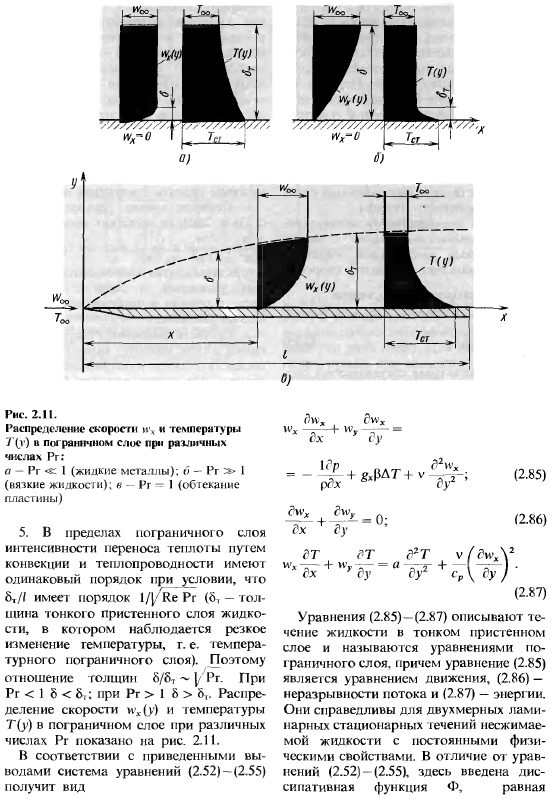
Распределение скоросгн и\ к темпера гуры 7’(г) в пограничном слое при различных числах Рг: а — Рг 1 (жидкие металлы); б — Рг » 1 (вязкие жидкости); в — Рг I (обтекание пластины) 5. В пределах пограничного слоя интенсивности переноса теплоты путем конвекции и теплопроводности имеют одинаковый порядок при условии, что 6,// имеет порядок 1/[ Re Рг (6, — толщина тонкого пристенного слоя жидкост, в котором наблюдается резкое изменение температуры, г. е. температурною пограничного слоя). Поэтому отношение толщин 8/8₇ ~ | Рг. При Рг 1 ё S.: при Рг > 1 8 > 8,.

Распределение скорости нх(у) и температуры Т(у) в пограничном слое при различных числах Рг показано на рис. 2.11. В соответствии с приведенными выводами система уравнений (2.52)-(2.55) получит вид ртЪс (2.85) (2.86) Уравнения (2.85) -(2.87) описывают течение жидкости в тонком пристенном слое и называются уравнениями пограничного слоя, причем уравнение (2.85) является уравнением движения, (2.86)-неразрывности потока и (2.87) — энергии. Они справедливы для двухмерных ламинарных стационарных течений несжимаемой жидкости с постоянными физическими свойствами.

В отличие от уравнений (2.52)- (2.55), здесь введена диссипативная функция Ф, равная ЛгЛ² Sy) и появляющаяся при выводе уравнения энергии (2.55), если при этом учитывается работа сил внутреннего трения, вызванного вязкостью жидкости или газа. Эта работа, в конечном счете, превращается в теплоту. Диссипация энер| ии потока — необратимое преобразование кинетической энергии жидкости в тепловую вследствие трения. Как показывает анализ, диссипативная функция должна учитываться в тех случаях, когда значение безразмерного комплекса (к — 1) соизмери- мо с единицей.

Это означает, что теплота, выделяющаяся при трении, играет существенную роль при условиях, когда скорость набегающего невозмущенного потока близка к скорости звука аж = tfkRT, а разность температур поверхности обтекаемого тела и потока | То — Тп | = (АТ)о имеет один порядок с температурой 7^. Уравнения пограничного слоя (2.85) — (2.87) содержат три неизвестные функции wₓ(x, у), wy(x, у) и 7(х, у). Они проще уравнений (2.52)—(2.55) и при ламинарном течении жидкости в пограничном слое могут быть рещены различными методами. Граничные условия к системе уравнений (2.85)—(2.87) зависят от постановки задачи.

Пусть, например, движение жидкости вдоль тонкой плоской пластины характеризуется большими числами Re, но течение в пограничном слое остается ламинарным, т. е. Reₓ ReK » (w^x/v),. (При обтекании пластины 3,2 • 10⁵ ReK Ю⁶.) Если, кроме того, пренебречь влиянием свободной конвекции (^хрА7 ==0), то уравнения (2.85) и (2.86) можно решить независимо от (2.87). Граничные условия к системе уравнений (2.85), (2.86) имеют вид: н’х = wy = 0 при у = 0; при у = со (см. рис. 2.9,»). Условия прилипания (wₓ = 0 при у = 0) выполняются при Mcr7|/Reₓ 0,01, т. е. когда среду можно считать сплошной; здесь Reₓ = w’oex/v. М» — Wix/ykRT^. При течении вдоль пластины dp/dx = 0.

Для решения уравнений (2.85) и (2.86) следует ввести вместо х и у новую безразмерную переменную г) = = И h»,/(vx), а вместо wₓ и ну новую неизвестную безразмерную функцию /(и) = Ф(х, уЭД/и^х, что позволяет перейти от уравнений в частных производных (2.85) и (2.86) к одному обыкновенному дифференциальному уравнению. Здесь ф (х, у) — функция тока, связанная с компонентами вектора скорости соот-£ф? ф ношениями н’х=—, ю, = — Величи- ну * ?х на ф характеризует объемный расход жидкости в точке с координатами х, у. ^²ф?²ф Так как, , — » , ^0, после введения dydx cxdy функции тока можно исключить уравнение неразрывности (поскольку оно при этом удовлетворяется). Если теперь заменить переменные, то получим 2/’» + УУ» = 0, (2.88) где f = У (т|) — безразмерная функция тока.

В новых переменных граничные условия принимают вид: У = У’ = 0 при т] = 0; f = 1 при Г) = ос. Это следует из формул перехода к новым переменным н’х = гф/гу = (?ф/гп)(?п/гу) = = «/’01); И’у=^?ф/?х=о,5 Уравнение (2.88) решается путем разложения /(т]) в ряд или численным методом, и решение представляется в виде таблицы, из которой, в частности, следует, что при г|=0 f» (п) = 0,3321, а при q = 5 /’(л) = н’х/м’ж = 0,9916. После подстановки У»(0) в выражение (2.84) находится касательное напряжение трения в сечении х на поверхности пластины Тст(х) = g(dwₓ/dy)cT = или tCT(x)/pw — O332fl/Re» где Reₓ = «vwx/v.

Сопротивление трения при обтекании пластины И; = b J t»(x)dx = 0,664bwTO /рр/ите, о где b — ширина, а / — длина пластины (см. рис. 2.11). По мере увеличения у скорость wₓ асимптотически стремится к н’од. Поэтому условно считается, что толщина динамического пограничного слоя соответствует такому значению координаты у, при котором и’х отличается от на 1%. Так как tj = у/(vx), при wₓ = 0,99и-го толщина пограничного слоя 5%5|/vx/w». При известных f, f и f можно перейти к решению уравнения энергии (2.87).

С учетом выражений (2.89) уравнение (2.87) можно представить в следующей форме: а²г/ат]² + о^рг [/(n)J(rfr/^) = «-Pnv^[r(n)j7^ (2.90) Общее решение уравнения (2.90) ищется в виде суммы общего решения соответствующего однородного уравнения [уравнения (2.90) с нулевой правой частью] и частного решения уравнения (2.90) — неоднородного уравнения. После перехода к безразмерной температуре однородное уравнение примет вид j²e₁/rfn²+o,5Pr[/(n)l(^eI/an)=o, (2.91) где 0₁(п) = [Т₁(п)-П,1/(7’ст-Гос) -его общее решение. Неоднородное уравнение J²0₂/Jq² + 0^Pr [/(пЛИЪ/^п) = = — 2Pr[/«(q)]², (2.92) где 0₂(п) = [(п)—частное решение. Общее решение уравнения (2.90) т(п) — Тк — С01 (n) + 0,5vv² е₂ (Т])/Ср. (2.93) .

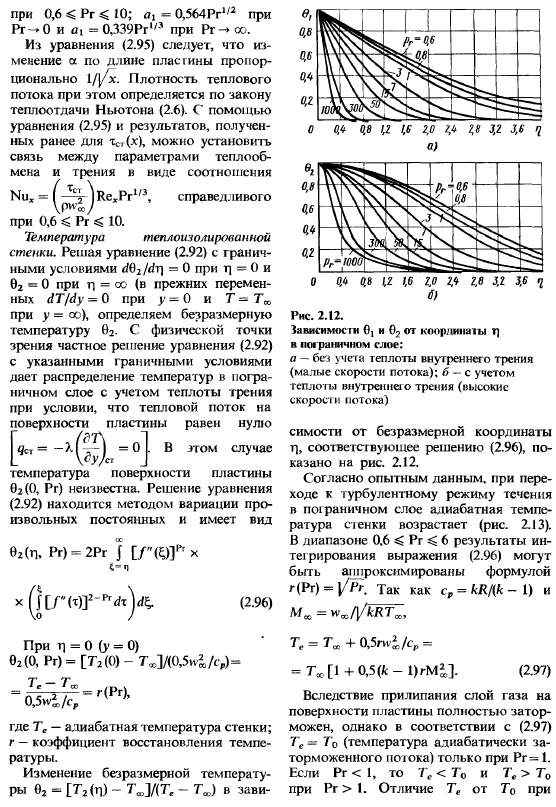
Теплоотдача пластины без учета теплоты трения. Безразмерная температура 01 может быть определена из уравнения (2.91) при следующих граничных условиях: 0х = 1 при q = 0; 0j = 0 при т) = оо (Г = Тст при у = 0; Т = Тм при у = сс). Так как уравнение (2.91) не содержит правой части, в которую входит диссипативная функция, распределение температур в пограничном слое находится без учета теплоты iрения: e.(n, Pr)= J ГПЭГл/ц/’йЯ’Х; О — (^-)ₑᵣ=(°’³³2)p7f = = «i(Pr). (2.94) Согласно результатам решения изменения безразмерной температуры 01 = [Т1 (п) — Т’юДДТ’ст — 7’») по безразмерной координате q существенно зависит от числа Рг (рис. 2.12).

Из уравнения (2.94) следует, что при Рг = 1 01 (П) = (7 (П) — Т»)/(ТСГ — Т») = 1- — Г(п) = 1 — или (Т(п) — — ТСТ)/(ТЛ — Тет) = wₓ/ww, т. е. при р/р = Х/(срр) профили скоростей и тем- ператур в пограничном слое тождественно совпадают, a S = 5Т. При возврате к прежним переменным — | С-) = aₜ(T» — 1//(vx). (ах/Х) = [«1 (Рг)] |/WopX/v и Nuₓ = [а, (Рг)] Reₓ*⁵, (2.95) где а = а(х) — местный коэффициент теплоотдачи в сечении х; aₜ = 0,332Рг|/³ при 0,6 Рг 10; 71 = 0,564Рг¹/² при Рг —♦ 0 и 71 = 0,339Рг,/³ при Рг-» ос. Из уравнения (2.95) следует, что изменение а по длине пластины пропорционально 1//х. Плотность теплового потока при этом определяется по закону теплоотдачи Ньютона (2.6).

С помощью уравнения (2.95) и результатов, полученных ранее для ТсДх), можно установить связь между параметрами теплообмена и трения в виде соотношения Nuₓ = (-^-)ReₓPr¹/³, справедливого УрИ’се / при 0,6 Рг 10. Температура теплоизолированной стенки. Решая уравнение (2.92) с граничными условиями /в₂//т| = 0 при Г) = 0 и 0₂ = 0 при п = ос (в прежних переменных dT/dy = 0 при у — 0 И Т sa Т», при у = ос), определяем безразмерную температуру 0₂. С физической точки зрения частное решение уравнения (2.92) с указанными граничными условиями дает распределение температур в пограничном слое с учетом теплоты трения при условии, что тепловой поток на поверхности пластины равен [fe⁼-’-^®«⁼⁰} в этом нулю случае температура поверхности пластины 0₂(0, Рг) неизвестна.

Решение уравнения (2.92) находится методом вариации про извольных постоянных и имеет вид е₂(П. Pr) = 2Pr f [Г ©Г х х^[Г-р, Л^ (2.96) При т] = 0 (у = 0) 0₂(0, Рг) = [Т₂(0) — Тх]/((),5и£/с.)== 7 е — Та, 0,5и^/с. г(Рг), где Те — адиабатная температура стенки; г — коэффициент восстановления температуры. Изменение безразмерной температуры 0₂ «= [Т₂(т]) — тп]/(Те — Tₐⱼ) в зави- Рис. 2.12. Зависимое ш 0] и 0? от коорли1ипы Г) в по»-раничном слое: 7 — без учета теплоты внутреннего трения (малые скорости потока); б — с учетом теплоты внутреннею трения (высокие скорости потока) симости от безразмерной координаты г), соответствующее решению (2.96), показано на рис. 2.12.

Согласно опытным данным, при переходе к турбулентному режиму течения в noi раничном слое адиабатная температура стенки возрастает (рис. 2.13). В диапазоне 0.6 Рг 6 результаты интегрирования выражения (2.96) могут быть аппроксимированы формулой г(Рг) = |/Рг Так как ср = kR/(k — 1) и = «vw/jArt7, Те = Та, + 0,5ги */?р = = Тсо[1+0,5(Ь-1)гМ]. (2.97) Вследствие прилипания слой газа на поверхности пластины полностью заторможен, однако в соответствии с (2.97) Те — То (температура адиабатически заторможенного потока) только при Pr= 1. Если Рг 1, то Тс То и Тв > Tq при Рг > 1. Отличие Те от То при Рис. 2.13.

Завнсммостъ коэффициента восстановления температуры г₽2(Ге- 7w)cjw* от числа КеЛ = m’^x/v: 1 — экспериментальная; 2 — теоретическая Pr / 1 объясняется перераспределением энергии в пограничном слое. Теплоотдача пластины с учетом теплоты трения. Так как т=т», 040=1 при г) = 0, а 0₂ (0) = г, то из выражения (2.93) следует, что константа С = = (Тст — Тг), и общее решение уравнения (2.90) имеет вид Т(п) — Тк = (Тст — TJ0, (П) + + (0,5и^/ср)0₂(П); (2.98) С учетом теплоты, выделяющейся вследствие внутреннего трения, в соответствии с выражениями (2.98) и (2.1) = щ(Тст — Тв)Х/н»Дух). (2.99) .

Это означает, что при больших скоростях потока дст(х)есТст — Г. Из уравнения (2.99) следует: если коэффициент теплоотдачи определяется выражением » = fleI(■)/(то критериальное уравнение для расчета теплоотдачи сохранит вил (2.95). При этом в соответствии с принятым определением а Асг(х) = а(Тст — тд (2.100) Входящие в формулу (2.100) адиабатная температура Т, стенки и коэф фициент теплоотдачи а находятся из выражений (2.97) и (2.95). Формула (2.100) используется при больших скоростях потока, когда выделение теплоты, обусловленное внутренним трением, значительно.

Из уравнения (2.97) следует, что при малых скоростях, когда Мх с 1, Те » Тх, при этом формула (2.100) переходит в закон теплоотдачи Ньютона 7с,(х) = а(7’С| — 7’^®). Из полученного решения следует, что пластина охлаждается при 7ₜI > Т» т. е. при Т’ст — тл > |/Pr(w^®/2cₚ) = Те-ТЛ. Если Т» Те и — Тк у Рг(и£/2сД то пластина будет нагреваться. Например, для воздуха |/Рг(и1/2ср) = 26 К при = 250 м/с. Теплообмен при больших скоростях потока При высоких скоростях потока анализ процесса теплообмена необходимо осуществлять с учетом не только теплоты трения, но и сжимаемости газа, а также влияния изменения физических свойств газа в зависимости от температуры.

Уравнения (2.85) —(2.87) в этом случае усложняются. В частности, в уравнении энергии (2.87) появляется дополнительный член [wₓ(«fp/4x)J, учитывающий выделение теплоты вследствие работы сил давления. Распределение скорости и давления в поле течения вне пограничного слоя зависит от формы обтекаемого тела. В отличие от рассмотренной пластины на телах с криволинейным контуром продольный градиент давления dp/dx / 0. При этих условиях среди определяющих безразмерных комплексов появляются: число Маха; температурный фактор; безразмерный продольный градиент давления (или скорости); показатель адиабаты к = ср/ссн отношения типа (2.74).

Для решения уравнений ламинарною пограничного слоя используются различные точные и приближенные методы. Например, для тел со степенным законом изменения скорости во внешнем потоке удается получить точное решение. В случае использования приближенного метода интегральных соотношений уравнения пограничного слоя удовлетворяются только в среднем по толщине слоя. В общем случае для учета всех перечисленных выше факторов применяются методы численного решения уравнений пограничного слоя с помощью ЭВМ.

В сложных условиях, вследствие неизбежной схематизации реальных процессов, теоретические решения требуют определенного экспериментального уточнения, однако вносимые при этом поправки невелики. Результаты существующих теорети-wcxmx роддом# ладэ* .w- гут быть представлены в виде обобщенных зависимостей — критериальных уравнений подобия, которые используются при расчете теплоотдачи. Для расчета локальных коэффициентов теплоотдачи при безотрывном обтекании плоских и осесимметричных тел различной формы потоком высокой скорости может быть рекомендована следующая формула, справедливая при ламинарном режиме .

Течения в пограничном слое (при обтекании штуплен-ных тел 4,5 • 10⁶ RcK 6,5 • 10е): Nib = O^Re^PrK³ ) х \ РстРсг / (-0 / 2т ’ 1 (2.1 где Nuct = ахэф/Хст; Вес^итрстХэфДкт; ptᵣ = pi/(RTCT); параметры, отмеченные индексом (0), отнесены к температуре Т⁰> = 0,5(Гст + 7) + О,22о; о = 0,5(к — l)Mj; т = (dwᵢ/dx)(x/wₗ), х — криволинейная координата, направленная вдоль контура обтекаемого тела и отсчитываемая от точки начала разви тия пограничного слоя; индексом 1 отмечены параметры внешнего течения в сечении х, в котором предстоит вычислить коэффициент теплоотдачи а. Эти параметры, включая dwi/dx, предварительно определяются путем аэро-газодинамического расчета с учетом влияния головной ударной волны или скачка уплотнения.

Эффективная длина некоторой плоской пластины, на которой при параметрах внешнего течения и,, pi образуется такой же температурный пограничный слой, как и в сечении х данного тела с криволинейным контуром, Хчф= ( JPcjVVjK^X^’CPctWtR²), где R = R (х) — расстояние от плоскости (или оси) симметрии данного тела до точки поверхности тела с координатой х. Здесь лля рэсусда используется раяея-сгво инторальных тепловых потоков на пластине и рассматриваемом теле с учетом предыстории развития тираничного слоя. Формула для определения x^j, получена методом локального подобия и справедлива при Тст = const. Для случая Тст = Тст(х) существует более сложная формула.

В формуле (2.101) отношения, содержащие произведение рр и критерий Рг, учитывают изменение физических свойств газа в зависимости от температуры, а множитель в квадратных скобках — влияние продольного градиента давления dpi/dx=—piWi(dwi/dx) и температурного фак гора (TCt/TOi); TOi = = ’Г, (1 + 0,5 (А- — 1)М²). Для расчета (х) и Те используются формулы (2.100) и (2.97). При Re = (w».x/v) > 10⁶ течение в пограничном слое на пластине становится турбулентным и закономерности переноса импульса и энергии резко изменяются. В этих условиях решение задач теплообмена возможно лишь при ряде упрощающих предположений с использованием не только теоретических, но и экспериментальных данных.

Отсутствие рациональных теорий турбулентности объясняется чрезвычайной сложностью этих течений (рис. 2.14). Высокочастотные пульсации скорости, давления и температуры в турбулент- Рис. 2.14. Турбулентное течение в тираничном слое (визуализация) минарной формы течения в пограничном слое в турбулентную, а также интенсивность теплоотдачи. При наличии пульсаций в потоке появ- ных потоках существенно влияют на развитие течения. При анализе течения используются осреднепные во времени величины и’х, й-}, р, Т и пульсационные составляющие их, Иу, /Л Т. 11ри этом мгновенные значения скорост и, давления и температуры могут быть определены в виде сумм: wₓ = wₓ + wₓ; и>=»гу+и£; р = р + р’; Т= Т + Г.

Степень турбулентности с является одной из важных характеристик турбулентных течений. Она определяется соотношением е = [| 0,5 (н/ + H’/jJ/w, где нх² и и’.² — осреднепные во времени квадраты пульсационных составляющих скорости: и’а — скорость нсвоз-мущенного потока. Для простоты рассуждений все соотношения здесь записаны в двухмерном приближении. В действительности картина течения трехмерна. От значения е в набегающем на тело потоке существенно зависит критическое число Re, соответствующее переходу ла ляется дополнительное напряжение тре ния т, = — (рн’у)’н£ = тельный перенос и донолии- энергии q, = = (рн^Г = -К где щ и Ку — коэффициенты турбулентной (кажущейся) вязкости и теплопроводности.

Выражения для определения т, и qy .могут быть получены из уравнений (2.52) — (2.55) с осредненными значениями скорост и, давления и температуры. В приближении пограничного слоя эти уравнения имеют следующий вид: Степень турбулентности — отношение средней квадратичной пульсаций составляющих вектора скорости в данной точке к осредненной скорости невозмущенного потока. = (X + X.)|p + (M +■ Общее напряжение трения в турбулентном потоке состоит из напряжения трения, вызванног о молекулярной (р) и турбулентной (р.) вязкостью, поэтому т = (р + рг). Аналогично q — (Л. + ?У. На некотором расстоянии от стенки в турбунтном ядре р»р, и X Хт.

Вблизи стенки, в ламинарном подслое роль р и X становится существенной. В отличие от уравнений (2.85)-(2.87) уравнения турбулентного пограничного слоя, записанные для осредненных величин, кроме «ТХ, ivy и Т содержат неизвестные значения рг и >и, зависящие от пульсационных составляющих. В основе приближенных полуэмпири-ческих теорий турбулентного тепло- и массообмена лежат эмпирические гипотезы, связывающие кажущиеся вязкость и теплопроводность с осредненными во времени скоростями и температурами. Каждая из таких теорий содержит опытные константы и может быть исполь зована для расчета определенного вида турбулентного течения.

В настоящее время с помощью вычислительной техники на основе результатов непосредственных измерений турбулентных пульсаций изучаются различные модели турбулентности, позволяющие получить более детальную информацию о локальной структуре турбулентных течений. В основу приближенных методов расчета теплообмена при турбулентном течении положены универсальные зависимости распределения скоростей и температур в пограничном слое, установленные путем обработки опытных данных методами теории подобия.

В выражениях, аппроксимирующих эти закономерности для скоростей, температур и линейных размеров, подобраны соответствующие масштабы, а константы не зависят от Re. Такой подход в сочетании с теоретическим обоснованием позволяет получить уравнения типа (2.101), необходимые для расчета теплоотдачи. Для расчета локальных коэффициентов теплоотдачи при турбулентном режиме течения в пограничном слое на телах различной (]юрмы может быть использовано критериальное уравнение NuCT = 0,0296Re°;⁸Pr?;⁴³ х х (7’ст/7е)°-⁴[1 + 0,5(Л — 1)гтМ?]⁰ П. (2.102) Это уравнение справедливо для случаев обтекания плоских и осесиммет ричных тел потоком, движущимся с высокой схоросгью, с продольным градиентом давления (в том числе при течении в соплах).

Критерии подобия построены точно так же, как и в формуле (2.101). В безразмерные комплексы Nile, и Recr входит величина х-ф — X =1 pCTw! R ⁵/⁴ (ix/(pcₗWi R ⁵/⁴). Коэффициент восстановления температуры (при турбулентном режиме течения) гт зависит практически только от критерия Рг: гт ~ j/Pr. Полуэмпирическая формула (2.102) согласуется с результатами измерений при 0,1 Т»{ТГ 1. Она справедлива в диапазоне 2,5 Мж, 4,5 на пластине и конусе и 6 М«> 10 при течении в соплах. Теплообмен при естественной конвекции Естественные свободно конвективные течения возникают под действием разности плотностей, как правило, связанной с неоднородностью температурного поля в жидкости, находящейся в поле внешних массовых сил.

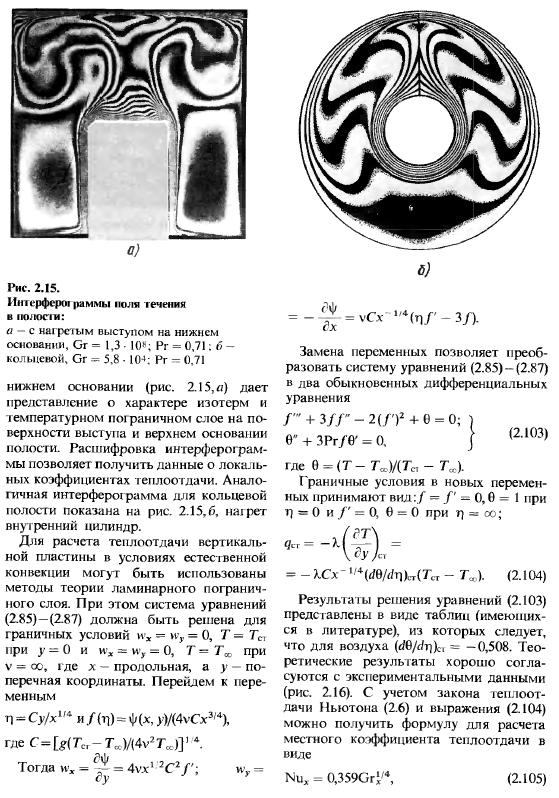
Для изучения таких течений, часто встречающихся в природе и технике, применяются как теоретические, гак и эксперимент; ->ьные методы. Интерферограмма ноля течения при естественной конвекции в прямоугольной полости с нагретым выступом на О) Рис. 2.15. Интерфсро! |шммы ноля течения в полости: а — с нагретым выступом на нижнем основании, Gr = 1,3-10*; Рг = 0,71: б — кольцевой, Gr = 5,8 ■ 10⁴: Рг — 0,71 нижнем основании (рис. 2.15, а) дает представление о характере изотерм и температурном пограничном слое на поверхности выступа и верхнем основании полости.

Расшифровка интерферограммы позволяет получить данные о локальных коэффициентах теплоотдачи. Аналогичная интерферограмма для кольцевой полости показана на рис. 2.15,6, нагрет внутренний цилиндр. Для расчета теплоотдачи вертикальной пластины в условиях естественной конвекции могут быть использованы методы теории ламинарного пограничного слоя. При этом система уравнений (2.85)—(2.87) должна быть ретена для граничных условий и-х — «vy = 0, Т = Тс, при у —0 и их = иу = 0, Т=ТХ при v = оо, где х — продольная, а у — поперечная координаты. Перейдем к переменным n = Q/x, u и/(П)=ф(х, y)/(4vCx³’⁴), где C=|>(TCᵣ-Tₜₜ)/(4v²rc)]’ *. Тогда н’х = 5 = 4vxl-²C²/’; wy = б) ‘’⁴(п/’-з/).

Замена переменных позволяет преобразовать систему уравнений (2.85)-(2.87) в два обыкновенных дифференциальных уравнения /’» +3//’— 2 (/’)+0 = 0; 6″ + ЗРг/6′ = 0. (2.103) где 0 = (Т-Та)/(Тс- TJ. Граничные условия в новых переменных принимают вид:/ = /’ — 0,0 = 1 при т) = 0 и /’ = 0, 0 = 0 при 7) = оо; = — ХСх-¹/⁴(^пЫТсг — Т. Л (2.104) Результаты решения уравнений (2.103) представлены в виде таблиц (имеющихся в литературе), из которых следует, что для воздуха (Ю//т))ст = −0,508.

Теоретические результаты хороню согласуются с экспериментальными данными (рис. 2.16). С учетом закона теплоотдачи Ньютона (2.6) и выражения (2.104) можно получить формулу для расчета местного коэффициента теплоотдачи в виде Nu, = 0,359Gr’⁴, (2.105) где Nuₓ = ахД; Grₓ = ^хлр(Тсг- Toc)/v²; Рг = 0,73. Из формулы (2.105) следует, что аоо1/х¹, ⁴ и уменьшается в направлении движения среды. Приближенный метод решения этой же задачи позволяет вывести зависимость Nu, = 0,508 [Pr/(Pr + 0,952)]’/⁴Raiz\ (2.106) которая в пределах 10″² Рг 10³ согласуется с точным решением с погрешностью, не превышающей 10%.

Здесь Ках определяется соотношением (2.72). Формулы (2.105), (2.106) применимы при Raₓ 0,7- К)⁹, г. е. при ламинарном режиме течения в пограничном слое. Аналогичное аналитическое решение для горизонтального цилиндра: Nuₓ = 0,604/ (p)Gri/⁴ (x/d)¹’⁴, (2.107) где Nuₓ = axfk; /(ф) — функция, зависящая от центрального угла ф; х — координата, отсчитываемая от передней критической точки вдоль контура цилиндра; Grₓ = gPx³(TCT — Tₐ)/v²;d — диаметр цилиндра. Значения /(ф), полученные из решения, приведены ниже. 0 30 60 90 0,760 0,752 0,718 0,664 120 150 165 180 0.581 0,458 0.36 0 Формула (2.107) справедлива при Raₓ0,710⁹ и Рг = 0,73.

Влияние на теплообмен числа Рг можно определить, пользуясь соотношением (Nuₓ/Gr‘Z⁴)/(Nuₓ/Gry⁴)Pf .0.73 ~ = [2,21/(1,143 + Рг)]’’⁴Рг|/². (2.108) Для расчета теплоотдачи при турбулентной естественной конвекции на вертикальной пластине могут быть использованы полуэмпирические формулы Эккерта и Джексона, полученные на основании экспериментальных данных о распределении скоростей и температур Рис. 2.16. Зависимость безразмерной температуры 0 = (Г- ГооХСТст — Та>) ш координаты ц при Рг = 0,73: • — х = II см; + -х = 7 см; х — х = 4 см; □ — х = 2 см; А — х = 1 см; О — х = 0,3 см в пограничном слое. При выводе формул физические свойства среды (X, с, р, ц и р) принимались постоянными.

Для местных и средних коэффициентов теплоотдачи эти формулы имеют вид Nuₓ = 0,0295Ra²/⁵Pr¹/¹⁵(l +’ + 0,494Pr²/³)²/⁵; __ (2.109) Nuj = 0,0246Ra²’⁵Pr¹/¹⁵(l + + 0,494Pr²/³)²/⁵, где Nuₓ = otx/X; Raₓ = gx³P AT/(va); Nui = a//X; Ra₍ = g/³P AT/(va); / — длина пластины. Формулы хорошо согласуются с результатами эксперимента при 10⁹ Ra 10², 0,7 Рг 10 и применимы для криогенных жидкостей. В процессах теплообмена, протекающих в условиях естественной конвекции в замкнутых полостях, толщина пограничного слоя становится соизмеримой с размерами пространства, в котором протекает процесс, поэтому упрощающие предположения, принятые при выводе уравнений пограничного слоя, становятся неприемлемыми.

При анализе процессов переноса теплоты через прослойки и щели различной формы приходится рассматривать полную систему уравнений (2.52)—(2.55), которая для этих условий может быть решена разностными методами с помощью цифровых ЭВМ. Для удобства численного решения из уравнений движения (2.52)—(2.53) исключается давление и вводится функция би¹, е’и’х ₂. а) = ———— =—v ф, называемая вих- сх су ревой напряженностью. После несложных преобразований и введения функции тока ф система (2.52)-(2.55) получает вид Уравнение (2.110), называемое уравнением переноса вихрей, показывает, что изменение вихревой напряженности во времени и пространстве связано с диссипацией вихревой напряженности вследствие 1 рения и характером изменения температуры в поле течения.

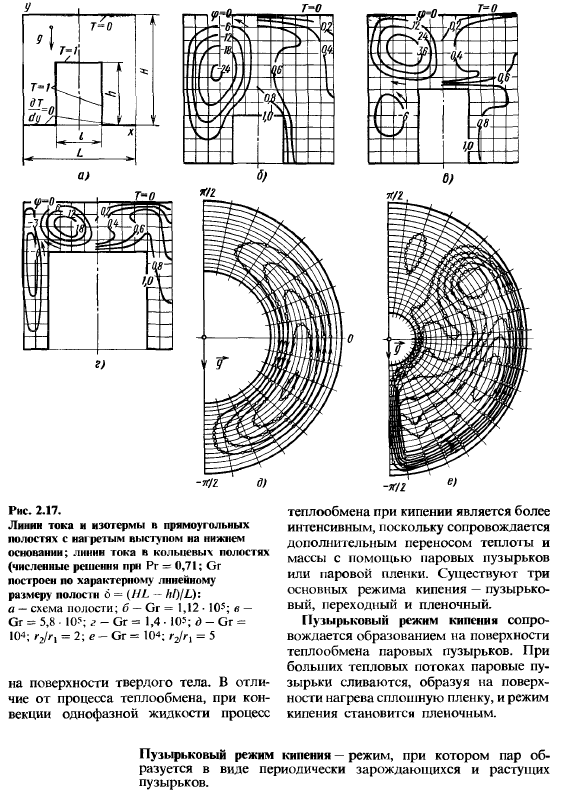
Решая эти уравнения с соответствующими начальными и граничными условиями, можно определить ф, о и Г, а затем wₓ и н-у. Линии тока (ф = const) и изотермы (Т = const), полученные в результате решения уравнений (2.110)—(2.112) для прямоугольной полости с нагретым выступом, показаны на рис. 2.17. Интенсивность теплообмена в рассматриваемых условиях зависит не только от критериев Gr и Рг, но и в значительной мере от относительных размеров полости. Этими факторами, в частности, определяется форма течения.

При первой, одновихревой форме течения (рис. 2.17, б) основное количество теплоты передастся о I вертикальной поверхности выступа, в то время как над горизонтальной поверхностью существует застойная зона. При второй форме с основным вихрем над выступом (рис. 2.17,») интенсивный конвективный теплообмен наблюдается над выступом, и теплоотдача определяется горизонтальной поверхностью. В случае третьей двухвихревой формы течения (рис. 2.17, г) теплоотдача верхней и боковой поверхностей выступа примерно одинакова.

Путем численного решения уравнений (2.110)-(2.112) для кольцевых полостей получена формула Nu = 0,134(ln r₂/rₜ)(rJ + + 0,362) Ra’U94exP(-opi/?j (2.113) хорошо согласующаяся с данными непосредственных измерений (см. рис. 2.15,6). Она применима при 2-10⁴Ra 0,5 • 10°; Рг > 0,7 и 2 r₂/ri 6; Ra = g6³₽ | 7\ — Т₂ | /(vfl); rₜ =r₁/8; б = = r₂ — rjjexpl-O. Ol/r.) = е-0М; Г]₎ r₂ и Tᵢₜ T₂ — радиусы и температуры внутренней и внешней поверхностей, образующих кольцевое пространство. Физические свойства среды отнесены к температуре 0,5(Т} + Т₂). Тепловой поток, проходящий через кольцевой слой, определяется по формуле Q = 2n(Tᵢ — T₂)NuX//(lnr₂/ri), где / — длина коаксиальных цилиндров, образующих полость.

Линии тока в кольцевых полостях показаны на рис. 2.17,б. е (Т₂> Tj). Существуют также формулы для расчета теплообмена при естественной конвекции в плоских и сферических полостях. Теплообмен при изменении агрегатного состоянии вещества Теплообмен при кипении. В процессе кипения происходит интенсивное парообразование во всем объеме кипящей жидкости с образованием паровых пузырьков. Этот процесс протекает при температуре насыщения Тц или несколько превышающей это значение и сопровождаемся поглощением теплоты фазового перехода. Различают кипение жидкости в большом объеме и кипение Of -!l д) Рис. 2.17.

Линии тока и изотермы н прямоугольных полостях с ка1 ретым выступом на нижнем основании; линии тока в кольцевых полостях (численные решения при Рг -=0,71; Gr построен по характерному линейному размеру полости 6 — (HL — hf)ILY. а — схема полости; б — Gr = 1,12 • 10s; в — Gr = 5,8 • IO?; г — Gr = 1,4 • 10?; д — Gr = К)⁴; rj/r, = 2; е — Gr = 10⁴; г₂/г₁ = 5 на поверхности твердого тела. В отличие от процесса теплообмена, при конвекции однофазной жидкости процесс теплообмена при кипении является более интенсивным, поскольку сопровождается дополнительным переносом теплоты и массы с помощью паровых пузырьков или паровой пленки. Существуют три основных режима кипения — пузырьковый, переходный и пленочный.

Пузырьковый режим кипения сопровождается образованием на поверхности теплообмена паровых пузырьков. При больших тепловых потоках паровые пузырьки сливаются, образуя на поверх-н(х_’ги нагрева сплошную пленку, и режим кипения становится пленочным. Пузырьковый режим кипения — режим, при котором пар образуется в виде периодически зарождающихся и растущих пузырьков. Пленочный режим кипения характеризуется меньшей интенсивностью теплоотдачи, чем пузырьковый.

Кипение возможно при условии некоторого nepei рева жидкости относительно температуры насыщения, при наличии центров парообразования. Минимальный радиус парового пузырька в момент зарождения соответствует размеру неровностей на поверх* ностнтеплообмена. Чем больше перегрев жидкости и чем выше давление р, гем меньше Кк. Если жидкость смачивает стенку, кипение протекает при незначительном перегреве. Это означает, что на образование пузырей помимо перегрева и давления влияет также характер физико-химического взаимодействия жидкости с твердой стенкой. Число действующих центров парообразования увеличивается с уменьшением Poor числа центров парюбразования приводит к увеличению интенсивности теплоотдачи за счет перемешивания жидкости при движении пузырьков.

На поверхности нагрева = 2с / н/[грп(Тст Т’н)]» где с — коэффициент поверхностного натяжения. Показано, что работа, которую необходимо затратить на образование пузырьков, уменьшается по мере увеличения перегрева жидкости. Поэтому вероятность вскипания увеличивается с ростом температурного напора АТ=ТСТ-ТН. Скорость роста паровых пузырьков является одной из основных характеристик процесса кипения и зависит от безразмерного комплекса СжАТр^Дгро), где г — скрытая теплота парообразования; сж — массовая удельная теплоемкость жидкости; рж и р» — плотность соотвегственно жидкости и пара.

Скорость роста пузырьков повышается но мерс увеличения этого комплекса. Это особенно заметно при низких давлениях. Паровой пузырек отрывается от поверхности нагрева и всплывает при определенном диаметре, который зависит от способности жидкости смачивать поверхность. Жидкость, нс смачивающая поверхность, оттесняется от нее, и интенсивность теплоотдачи уменьшается. Теплоносители, обычно применяемые в теплоэнергетических установках, а также криогенные жидкости смачивают металлические поверхности. К несмачивающим жидкостям относится, например, ртуть. Процесс теплоотдачи от перегретой жидкости к поверхности оторвавшегося пузырька отличается высокой интенсивностью.

Турбулизация парожидкостной смеси движущимися пузырями существенно сказывается на интенсивности теплоотдачи только при небольших АТ. Интенсивность теплоотдачи при пузырьковом кипении в основном определяется толщиной ТОНКОЙ ЖИДКОСТНОЙ прослойки, остающейся непосредственно на поверхности теплообмена вследствие смачивания. Линия, характеризующая зависимость теплового потока от температурного напора, называется кривой кипения. На рис. 2.18 зависимость плотности ц теплового потока от -температурного напора АТ представлена в логарифмической системе координат. Область / на этом графике соответствует конвективному теплообмену. В области 2, благодаря малой плотности центров парообразования, процесс кипения неустойчив.

Область 3 соответствует развитому пузырьковому режиму кипения. В этой области плотность ц тепловог о потока достигает максимума. Дальнейшее повышение перегрева жидкости приводит к появлению переходной области 4, а затем Пленочный режим кипения — режим, при котором на поверхности нагрева образуется сплошная пленка пара, периодически прорывающегося в объем жидкости. Емс. 2.18. Зависимость плотности теплового потока q от температурного напора ДГ в леи арнфмическон системе координат Тст = const такого скачка нс наблюдается.

На интенсивность теплообмена при кипении существенное влияние оказывают давление, теплофизические свойства жидкости, параметры шероховатости поверхности нагрева и теплофизические свойства стенки. К последним относится комплекс, называемый коэффициентом аккумуляции теплоты, |/1ср. Зависимость комплекса А = от безразмерного дав ления р/р» при кипении различных жидкостей показана на рис. 2.19. Величина (ot/yc’⁷)p- вычислена при условном давле- области 5 устойчивого пленочного кипения.

В области 6 становится существенным перенос теплоты излучением. При низких давлениях и тщательной дегазации жидкости область / конвективного теплообмена может быть расширена, и зависимость /(ДТ) будет соответствовать линии ЛБ (рис. 2.18). В случае несмачивающих жидкостей пленочный режим кипения может появиться при небольших АТ (линия ВГ). Характер кривой кипения может также резко измениться при изменении граничных условий. Так, при обогреве поверхности теплообмена электрическим током (цст — const) наблюдается скачкообразный переход пузырькового режима кипения в пленочный.

При условии нии Р* = О. ОЗрк. При Р, близких К Рк, влияние давления резко возрастает. Ко личественные закономерности зависят также от гидродинамической структуры двухфазного потока, которая при кипении отличается большим mhoi ообразием. В условиях недогрсва жидкости возможно поверхностное кипение. Строгого математического описания процесса теплообмена при кипении пока не существует. В большинстве случаев связь коэффициента теплоотдачи с числом Рве. 2.19. Зависимость комплекса от безразмерного давления р/рк при кипении различных жидкостей центров парообразования, частотой отрыва пузырей, физическими свойствами жидкости и другими факторами устанавливается экспериментально.

Расчет теплоотдачи при пузырьковом кипении жидкости в большом объеме в условиях свободного движения можно выполнить, воспользовавшись следующим приближенным уравнением подобия: Nu » 0,082К?’³³К£-⁷Рг»°-⁴⁵, (2.114) где Nu = К- = (JVxATpJ/^firp,.); Kq — ?§²/(р,, гОж0; Рг = Уж! ал\ 6 = = I а — рп) — капиллярная постоянная; АТ = Тс, — Т» — температурный напор; / = (cₓCTp»TH)/(rp»)² = = /?кСж ATpi-/(2rpn) — некоторый характерный размер, пропорциональный радиусу R; о — коэффициент поверхностного натяжения на границе жидкость — пар; Кг и К, учитывают число центров парообразования и частоту отрыва пузырей.

Если пренебречь влиянием ускорения свободного падения, то можно получить более простое уравнение для расчета теплоотдачи Nu = CRcⁿPrm, где Nu = а//Хж; Re = h7/vw; w = y/(rpₙ) -приведенная скорость парообразования. Значения С, m и п найдены путем обработки большого числа экспериментальных данных, полученных при кипении различных жидкостей. Для неметаллических теплоносителей С = 0,0625, п = 0,5, m = 0,33 при Re 0,01; С = 0,125, и = 0,65, т — 0,33 при Re > 0,01; для жидких металлов С = 0.125, и = m = 0,65, Re > 0,01. Пределы применимости этого уравнения: 10″ ⁵ Re 10⁴; 0,86 Рг ^7,6; ю7 м/с.

При плотности теплового потока, большей первой крити ческой /к, чистая форма пузырькового кипения невозможна. Первая критическая плотность теплового потока для неметаллических теплоносителей с малой вязкостью Чч = кг |/р, /^л(рж — рп)(0,13 к 0,16). В литературных источниках имеются данные, необходимые для расчета теплообмена при кипении и в других условиях: при пленочном и переходном режимах, в условиях вынужденного течения, в ограниченном объеме (в том числе в различно ориентированных трубах и каналах).

Теплообмен при конденсации пара. Конденсация протекает с выделением теплоты и всегда сопровождается теплообменом Явление теплообмена при конденсации встречается в конденсаторах паротурбинных, холодильных и опреснительных установок, теплообменных аппаратах и других устройствах. Наиболее характерной для этих установок являст-ся поверхностная конденсация пара, реже встречается явление конденсации во всем объеме. Конденсация насыщенного или перегретого пара на поверхности твердого тела возможна, если температура поверхности Тсг Тн. Конденсация жидкости на твердой поверхности начинается в углублениях или трещинах.

Пленочная конденсация возникает на смачиваемой поверхности. Теплота, выделяющаяся на поверхности раздела фаз, отводится в стенку через пленку конденсата. В процессе конденсации температура Т» поверхности жилкой пленки остается несколько ниже температуры Т» насыщения. Для обычных и криогенных жидкостей Тп незначительно отличается от Ти. Термическое сопротив Первая критическая плотность теплового потока — максимально возможная (при данных условиях) плотность теплового потока при пузырьковом кипении. Пленочная конденсация — образование сплошной пленки конденсата на смачиваемой поверхности. ление при передаче теплоты от пара к стенке равно сумме термического сопротивления пленки конденсата и термического сопротивления, связанного со скачком температуры на границе раздела паровой и жидкой фаз.

При заданной разности температур пара и стенки интенсивность процесса теплообмена при пленочной конденсации определяется условиями отвода конденсата с поверхности и режимами течения пленки и пара. Термическое сопротивление пленки зависит от ее толщины, теплопроводности жидкости, степени турбулизации потока и наличия поверхностных волн. Капельная конденсация возникает на несмачиваемой поверхности и имеет коэффициент теплоотдачи на порядок выше, чем пленочная. Для получения капельной конденсации на поверхность теплообмена наносятся специальные покрытия.

Использование капельной конденсации позволяет значительно сократить 1абариты и массу конденсаторов. Примеси неконденсирующихся газов в паре существенно снижают интенсивность теплоотдачи при конденсации. В большинстве практически важных случаев приходится иметь дело с пленочной конденсацией. Средний коэффициент теплоотдачи при пленочной конденсации неподвижного насыщенного пара на плоской поверхности длиной L может быть вычислен по следующей приближенной формуле: = (2|/2/3)(GaKPrsin 0)¹’⁴, (2.115) где Nu = а£Дж; Ga = ^Ь³Рж(рж-р»Ур²ж; К = г/сж(Т» — Тст); Рг = уж/аж; 0 — угол наклона поверхности к горизонту; г — эффективное значение теплоты парообразования; г = г + 0,68сж(Т» — Тст) при сж(Т» — Тс.)/г 2.

Путем введения г* учитывается не- догрев пленки и отклонение профиля температуры в пленке от линейного. При выводе формулы (2.115) предполагалось, что режим течения пленки ламинарный, пар не содержит примесей, а влиянием термического сопротивления на границе пленки с паром, конвективным переносом теплоты через пленку, действием сил инерции и трением на границе раздела фаз можно пренебречь. Вывод основан на решении уравнений d²Tldy² = 0, рж(/²и’х/ау²) = -ри&с описывающих теплообмен в пленке. Образование на поверхности пленки волн уменьшает ее толщину и повышает интенсивность теплоотдачи.

При торможении же стекающей пленки паром уровень интенсивности теплоотдачи снижается. Опытным путем установлено, что при К > 5 и I Рг 100 влияние конвективного переноса теплоты и действие сил инерции пренебрежимо малы. Формула (2.115) становится пригодной для расчета теплообмена при конденсации пара на горизонтальном цилиндре, если положить 0 = я/2 и L = 2,780 (О — диаметр цилиндра), а также для расчета теплообмена при конденсации внутри коротких горизонтальных труб. В последнем случае 0 — л/2, L = fc,4d, где (I — внутренний диаметр трубы.

Для расчета теплообмена при конденсации пара на пучке горизонтальных труб, расположенных друг под другом, рекомендуется формула ~Nu = 0,728(1 +0,2(n- l)/Kl/⁴, (2.116) где п — число рядов труб. Формула (2.116) применима при (и — )К 2. Критерии подобия здесь построены точно так же, как и в формуле (2.115). За характерный размер принят наружный диаметр трубы. Капельная конденсация — образование капель конденсата на несмачиваемой поверхности.

Смотрите также:

Предмет теплотехника

Теплопроводность	Лучистый теплообмен
Численные методы решения задач теплопроводности	Топливо и его горение