Степени свободы плоской кинематической цепи

Степени свободы плоской кинематической цепи

• СТЕПЕНИ СВОБОДЫ ПЛОСКОЙ КИНЕМАТИЧЕСКОЙ ЦЕПИ Положение звена АВ (фиг. 14) в пределах плоскости определяется тремя параметрами: двумя координатами какой-либо точки этого звена и углом наклона звена к какой-либо из координатных осей. Свободное звено на плоскости, изменяя три параметра, исполь­зует три степени свободы, причем для достижения конечного резуль­тата является совершенно безраз­личным, используются ли эти три степени свободы сразу при слож­ном движении или поочереди в любом порядке.

Используя поочереди три сте­пени свободы при плоскопарал­лельном движении, звено может переместиться из положения АВ в другое заданное положение ab следующим образом: -1) продвинуться параллельно самому себе в направлении, парал­лельном оси X, до совпадения точки А с перпендикуляром, опущенным из точки а на ось х; в результате такого продвижения звено займет положение Л ^ ;2) из положения также параллельно самому себе продви­нуться в направлении, параллельном оси у, до совпадения точек Л2 и а; в результате такого продвижения звено займет

положение аВ2: 3) повернуться вокруг точки а до совпадения точек В 2 и Ь. Два не Людмила Фирмаль

связанные между собой звена в плоскопараллельном дви­жении располагают шестью степенями свободы, которые могут быть использованы для перемещения этих звеньев из любых заданных поло­жений в любые другие заданные положения. Два связанные в кине­матическую пару звена в абсолютном плоскопараллельном движении, т. е. без изменения своего относительного расположения, могут исполь­зовать только те три степени свободы, какими располагает одно звено. Но, будучи связанными в кинематическую

пару, звенья не утрачи­вают свободы относительного перемещения: звенья вращательной пары могут использовать еще одну степень свободы на поворот одного звена вокруг центра’ пары, а звенья поступательной пары— на скольжение одного звена по другому. В отличие от звеньев низших пар звенья высшей пары при относительном перемещении их могут использовать две степени свободы — одну на скольжение и другую — на качение одного звена по другому. Следовательно, н и з ш а я п а р а отнимает от двух звеньев две степени свободы или, как иначе принято говорить, н а л а г а е т д в е с в я з и ; в ы с ш а я п а р а н а л а г а е т о д н у с в я з ь .

• Входя в состав машины, кинематическая цепь одним из своих звеньев должна быть жестко связана с корпусом машины. При одном неподвижном звене, называемом стойкой, структурная формула пло­ской кинематической цепи получает следующий вид Зп — 2 p k = W, (1) где п — число подвижных звеньев или число всех звеньев, за исклю­чением одного, обращенного в стойку; р — число низших пар; k — число высших пар; № — число степеней свободы или число свободных параметров. Число степеней свободы кинематической цепи относительно непо­движного звена в отличие от числа степеней свободы цепи без непо­движного звена называется степенью

подвижности кинематической цепи. В дальнейшем кинематические цепи без неподвижных звеньев нами не будут рассматриваться. При выводе формулы (1) предполагалось, что каждым звеном вносятся в кинематическую цепь три степени свободы, а каждой низшей парой отнимаются две. Но можно представить себе такую цепь, все звенья которой лишены возможности поворачиваться, т. е. изменять свои угловые параметры. Такой цепью является цепь, содержащая только поступательные пары. Входя в такую цепь, звено вносит в нее не три, а две степени свободы, а низшая кинематическая пара (в данном случае всегда поступательная) налагает не две, а одну связь.14 Структурный анализ плоских механизмов

Поэтому при определении числа степеней свободы кинематиче­ской цепи, содержащей только Людмила Фирмаль

поступательные пары, надо исходить из формулы W = 2п — р, (2) где W — число степеней свободы; п — число подвижных звеньев; р — число поступательных пар. Кинематические цепи, содержащие только поступательные пары, имеют практическое применение лишь в редких случаях. Числом степеней под­вижности, равным числу свобод н ых пар аметр ов, х ар актер изуется подвиж­ность кинематической цепи. При числе степе­ней подвижности, равном нулю, все звенья могут £ занимать только опреде­ленные положения, из ко­торых не могут быть выве­дены из-за отсутствия свободных параметров, т. е. из-за невозможности привести в дви­жение какое-либо из звеньев. При W степенях подвижности опре­деленное взаимное расположение всех звеньев достигается после таких движений одного или нескольких ее звеньев, при которых были

использованы все W свободных параметров. При непрерывном движении одной части звеньев, движущихся по заданным законам и использующих все свободные параметры, остальные звенья будут двигаться вполне определенно. Звенья, законы движения которых при исследовании цепи предпо­лагаются заданными, называются в е д у щ и м и , остальные звенья называются в е д о м ы м и . Не следует смешивать ведущих звеньев с теми звеньями, которые приводятся в движение внешними силами. Такие звенья в отличие от ведущих будем называть движущими. Ведущее звено может быть движущим, но может им и не быть. Для лучшего уяснения изложенного разберем несколько приме­ров. На фиг. 15 приведена схема трехзвенной цепи с

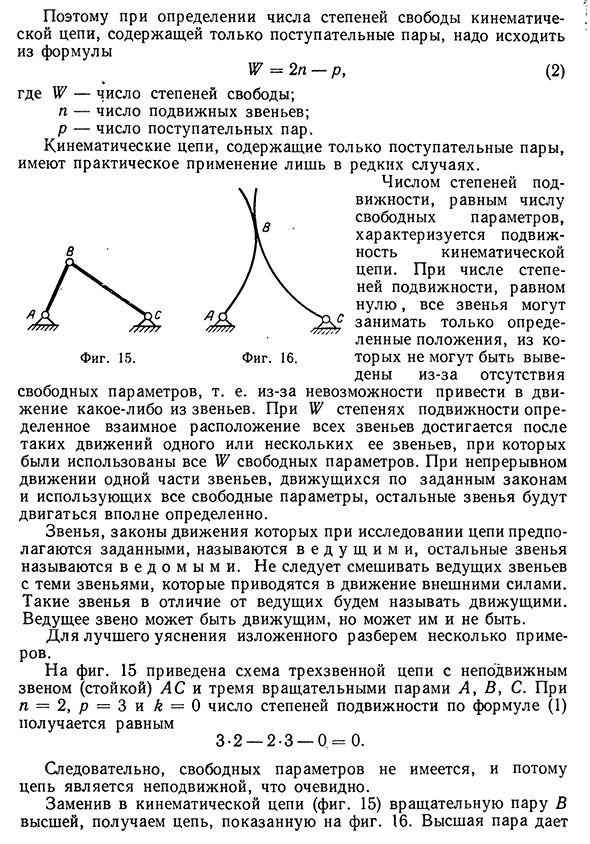
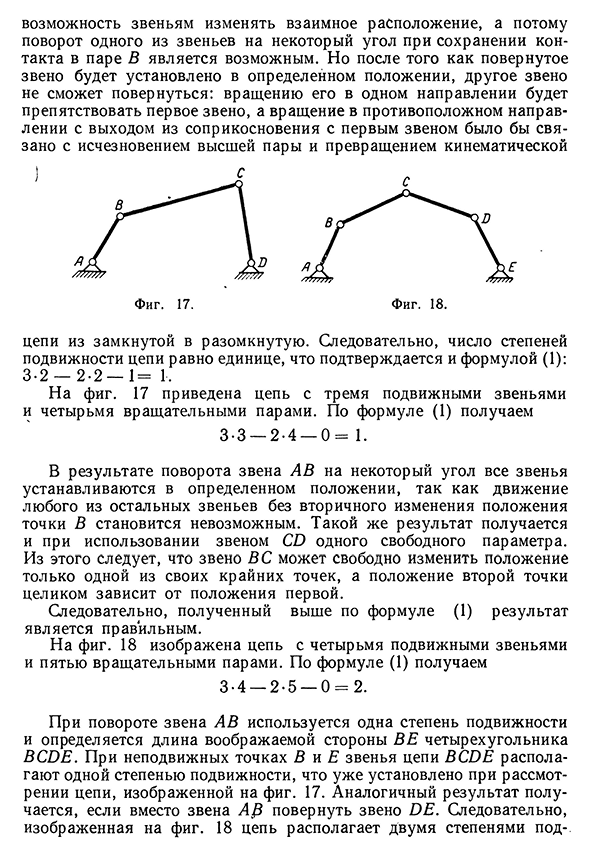
неподвижным звеном (стойкой) АС и тремя вращательными парами Л, В , С. При п = 2, р = З и ^ = 0 число степеней подвижности по формуле (1) получается равным 3.2 — 2-3 — 0 = 0. Следовательно, свободных параметров не имеется, и потому цепь является неподвижной, что очевидно. Заменив в кинематической цепи (фиг. 15) вращательную пару В высшей, получаем цепь, показанную на фиг. 16. Высшая пара даетСтепени свободы, плоской кинематической цепи lb возможность звеньям изменять взаимное расположение, а потому поворот одного из звеньев на некоторый угол при сохранении кон­такта в паре В является возможным. Но после того как повернутое звено будет установлено в определенном положении, другое звено не сможет повернуться: вращению его в одном направлении будет препятствовать первое звено, а вращение в противоположном

направ­лении с выходом из соприкосновения с первым звеном было бы свя­зано с исчезновением высшей пары и превращением кинематической цепи из замкнутой в разомкнутую. Следовательно, число степеней подвижности цепи равно единице, что подтверждается и формулой (1): 3-2 — 2-2 — 1= 1. На фиг. 17 приведена цепь с тремя подвижными звеньями и четырьмя вращательными парами. По формуле (1) получаем 3-3 — 2-4 — 0 = 1. В результате поворота звена АВ на некоторый угол все звенья устанавливаются в определенном положении, так как движение любого из остальных звеньев без вторичного изменения положения точки В становится

невозможным. Такой же результат получается и при использовании звеном CD одного свободного параметра. Из этого следует, что звено ВС может свободно изменить положение только одной из своих крайних точек, а положение второй точки целиком зависит от положения первой. Следовательно, полученный выше по формуле (1) результат является правильным. На фиг. 18 изображена цепь с четырьмя подвижными звеньями и пятью вращательными парами. По формуле (1) получаем 3.4 — 2-5 — 0 2 . При повороте звена АВ используется одна степень подвижности и определяется длина воображаемой стороны BE четырехугольника BCDE. При

неподвижных точках В и Е звенья цепи BCDE распола­гают одной степенью подвижности, что уже установлено при рассмот­рении цепи, изображенной на фиг. 17. Аналогичный результат полу­чается, если вместо звена АВ повернуть звено DE. Следовательно, изображенная на фиг. 18 цепь располагает двумя степенями под-16 Структурный анализ плоских механизмов вижности, что подтверждает правильность полученного по формуле (1) результата. В этой цепи каждое из звеньев А В и D E может использовать только один свободный параметр, каждое же из звеньев В С и CD, переходя в другое положение, использует два свободных параметра. Напри­мер, звено ВС, изменяя положение точки В, использует один свободный

параметр, потому что точка В, двигаясь по окружности с радиусом А В , может свободно изменять только одну координату; после же уста­новки точки В в новом положении точка С, двигаясь по окружности с радиусом ВС, может свободно изменять также только одну коор­динату. Поэтому все звенья изображенной на фиг. 18 цепи будут дви­гаться определенным образом или при двух ведущих звеньях А В и D E или при одном ведущем звене В С и CD. Таким образом, определив число степеней подвижности плоской кинематической цепи, мы можем решать вопрос о числе ведущих звеньев по-разному в зависимости от того, сколькими степенями подвижности располагают звенья, выбираемые в качестве ведущих. На практике в качестве ведущих всегда выбирают звенья с одной степенью подвижности. Поэтому число степеней подвижности плоской

кинематической цепи можно считать равным возможному числу ее ведущих звеньев. При этом одно из звеньев кинематической цепи обращается в стойку, а все остальные движутся по вполне определен­ным законам. Формула (1) даёт возможность, даже при сложной цепи, быстро решать вопрос о числе ведущих звеньев, необходимом для опреде­ленности движения всех ведомых звеньев.

Смотрите также:

Предмет Теория Машин и Механизмов ТММ

Кинематическая цепь	Механизм и машина
Кинематические схемы	Классификация механизмов