Оглавление:




Аналитический расчет простых рам
- Аналитический расчет простой рамы простая рама представляет собой геометрически инвариантную стержневую систему, состоящую из двух или трех стержней, соединенных с узлом жесткой связью. Для риса. 30.1 приведены несколько геометрических схем простого каркаса. Аналитический расчет рамы-изгибающий момент, поперечная и продольная силовые диаграммы structure…Is
определить три внутренних силовых фактора от внешних нагрузок. Участки M, Q и N строятся по геометрическим фигурам рамы, вдоль оси стоек и поперечины. На участке М, как правило, никаких знаков не ставится, а продольная ось изгибающего момента обязательно оттягивается от растянутого волокна. Вертикальная ось участка Q и N задается знаком по следующим правилам:если ее направление совпадает с вращением остальной части кадра по часовой стрелке, то горизонтальная ось равна горизонтальной оси.
Подробности объясняются в Примере. Например. О кадре, показанном на рисунке. Людмила Фирмаль
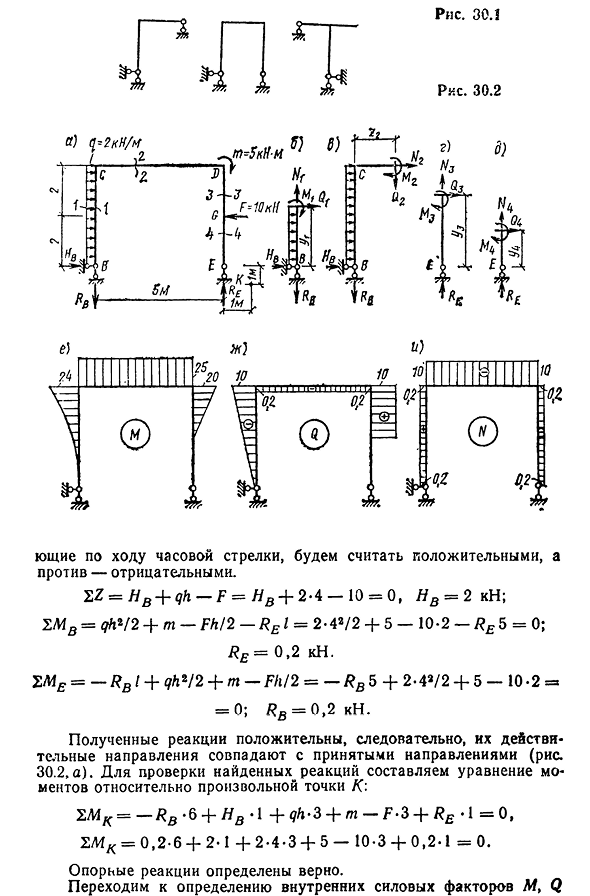
30.2, a, участок M, Q и N. Решение. Во-первых, давайте сделаем кинематический анализ. Этот кадр поддерживал три непараллельных и непересекающихся, прикрепленных к жесткому диску. Эта рамка неизменна. Определите эталонные реакции HB>Rb и Re. Момент, акт-333-1. Те, кто творит зло, Рис 30,2 Значения направления по часовой стрелке учитывают положительные и отрицательные значения. %З=НВ+qх-Ф=НВ+2-4-10=0, НВ=2кн;2L1B=qh42+м-Хабнарфьордюр!2-l=2-42/2 + 5 — 10-2 — re 5=0; re = 0,2 кн. ZME= — R B l — +qh*!2+tn-Fh / 2= — RB5+ 2-42/2 + 5 — 10.2 = = 0; /?b=0,2 в Н. Полученная реакция положительна, поэтому фактическое
направление совпадает с принятым (рис. 30.2, а). Чтобы проверить найденную реакцию, составьте уравнение момента о любой точке/ZMK= — RB-b+HB-l+^. 3+m-F. 3+^B. l= 0 , = 0 ,2 -6 + 2-1 + 2 — 4 — 3 + 5 — 10-3 + 0,2.1 = 0 . Реакции поддержки определены правильно. Перейдем к определению коэффициента внутренней силы L4, Q 334i Чтобы определить их, разрежьте раму в каждой силовой секции с поперечным сечением, перпендикулярным оси стержня, на две части. Отбросьте все детали и замените их на M, Q и N. В остальном мы
- составим три уравнения статического равновесия из всех сил, приложенных к этой части. В этом кадре находятся четыре силовые секции BC, CD, DG и GE,среди которых рисуют четыре секции: 1-1, 2-2, 3-3 и 4-4. Раздел 1-1. Оставляем части каркаса, расположенные ниже секции 1-1, а верхнюю часть отбрасываем(рис. 30.2, 6). В графической рамке произвольно запишите уравнения равновесия для изгибающего момента M[раздел 1-1] в положительном и по часовой стрелке направлениях. Поэтому момент от внешней силы, направленной по часовой стрелке, также считается положительным.
Это правило применяется ко всем остальным частям рамы. Значение и фактическое направление Afj определяются из выражения SA4°CT= / I, — HB yt-q tf / 2=0, Откуда он взялся М! =h vu1+w i / 2 — Поскольку изгибающий момент Mi положительный, левое волокно растягивается до Солнечной стойки. По длине стойки солнце изменяется по закону вторичной параболы, имея значение r/x=0= = y1=h=4 M {=MS V=2-4 2 * 42/2=24 кН*м. Величина и знак поперечной силы ци определяется по формуле проекций на ось, перпендикулярную оси Солнечной стойки. SZOCT= / 7B+^1+Q1=0, Откуда он взялся Qi= — n-YAU1 Боковая сила солнечной стойки
Qi отрицательна и изменяется по линейному закону: z/i=0Q1 = Qbc = — Людмила Фирмаль
2kN;d/1=/g=4Qi=QCB= — 2-4= — 10kN. Величина и знак нормальной силы Afj определяется из уравнения проекции на ось, параллельную оси Солнечной стойки,£US0ST= -/?B+Wi=0, где Ni=/?b=0,2 кн. Вертикальная сила U! В стойке VS положителен, эластичен и имеет постоянное значение. 2-2. Оставляем часть рамы, расположенную слева от секции 2-2, а правую часть отбрасываем(рис. 30.2, б). Величина и направление изгибающего момента м2 определяется из уравнения суммы моментов от всех сил, действующих на остальные детали относительно центра тяжести секции 2-2., 335 из ниоткуда M2=RB z2+H B h+qh42. Изгибающий момент м2 положительна и, следовательно, растягивается в Риге * Ле-это верхние волокна. Момент M2 изменяется по линейному закону и имеет значение: z2=0M2=M C d — =2-4 + 2*42/2 =24kN-m; z2=Z = 5m M£ = M dc= 0,2’5-}-2-4
+ + 2-42/2=25 кН-м Боковая сила Q2 определяется из уравнения проекции на ось, перпендикулярную оси перекладины CO: 2 \ OST= — RB—Q2=0, откуда (?2= — Rb=-0,2 кн. Поперечной силы Q2 на компакт-диске перекладина является отрицательным и имеет постоянное значение. Продольная сила N2 определяется из уравнения проекции на ось, параллельную оси поперечины CD. SZ oct= / / b+^ / z-fA^2=0, где M2== — HB-qh=—2—2-4= — 10кн. Продольная сила N2 поперечины CD отрицательна (т. е. сжатие) и имеет постоянную величину. Раздел 3-3. Мы отбрасываем верхнюю часть, оставляя нижнюю часть стойки EGD, потому что на нее воздействует меньшее количество внешних сил(см. Рисунок. 30.2, г). Величина и направление изгибающего
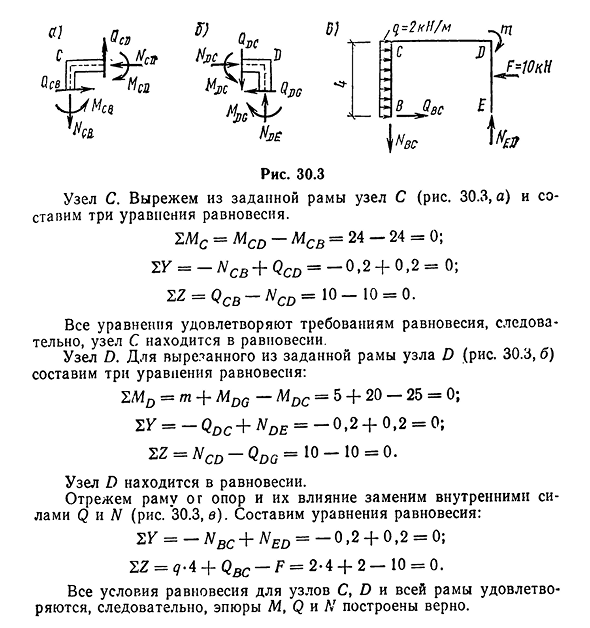
момента L43 определяется по формуле суммы моментов от всех сил, действующих на остальные, относительно центра тяжести секции 3-3. SM§CT= — F(y3-2)+MoH=0,где M3= — F (y3-2), 22=0; SZ=N CD-Qqq=10 10=0. Узел D находится в равновесии. Вырежьте раму из опоры и замените ее воздействие внутренними силами Q и N(рис. 30.3, в). Составим уравнение равновесия: SY= — N bc+Ne d= — 0 , 2 + 0,2 = 0; SZ=<7-4+Qbc-F=2-4 + 2 — 10 =0. Графики M, Q и N построены правильно, так как выполняются все условия равновесия для узлов C, D и всего кадра.
Смотрите также:
Решение задач по технической механике
| Кривая давления. Рациональная ось арки | Расчет на прочность и жесткость при кручении |
| Статически определимые плоские рамы. Общие сведения. | Изменение моментов инерции при параллельном переносе осей |

