Кривая давления. Рациональная ось арки

Кривая давления. Рациональная ось арки

• Кривая давления. На рациональную ось свода свода, как и в случае балки, действует внешняя нагрузка на одну из главных плоскостей инерции поперечного сечения. От внешней нагрузки в поперечном сечении трех шарнирных дуг возникают изгибающий момент, сжимающая сила, приложенная к центру, и боковая сила. В таком случае это соответствует внешнему сжатию центра в главной плоскости инерции. Изгибающий момент и центр силы сжатия

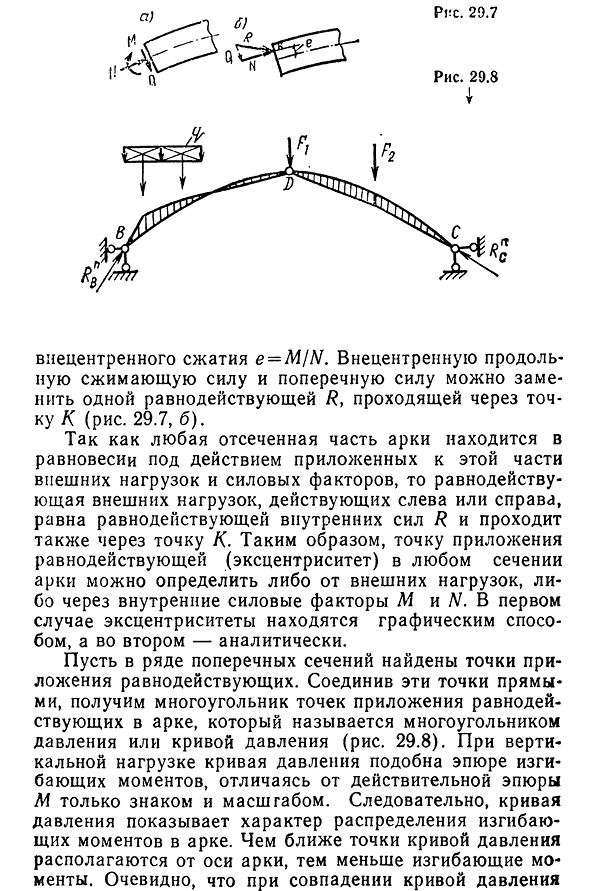
совместного действия в любом сечении свода, одна продольная сила сжатия отклоняется от центра, то есть расстояние е до 29,7, а) от центра тяжести поперечного сечения. Величина этого расстояния (эксцентриситета) определяется по известной формуле 329rx 29.7 Центр сжатия e=M / AZ. Смещенные от центра продольные сжимающие силы и поперечные силы могут быть заменены одним результатом/? Пройдите через точку K(рис. 29.7, б).

Так как отрезная часть свода находится в равновесии с действием внешней силы и Людмила Фирмаль

силового фактора, действующего на эту часть, то внешняя нагрузка, действующая слева и справа, равна результату действия внутренней силы R и проходит через точку L. Полученную точку приложения можно найти в нескольких разделах. Соединяя эти точки прямой линией, вы получаете многоугольник точек приложения результирующей функции в дуге (это называется многоугольником давления или кривой давления). 29.8). При вертикальной нагрузке

кривая давления напоминает график изгибающего момента и отличается только знаком и масштабом от фактического графика м. Таким образом, кривая давления указывает на распределение изгибающего момента в своде. Чем ближе точка кривой давления к оси дуги, тем меньше изгибающий момент. Кривая давления соответствует Ось дуги, которая совпадает со всеми кривыми давления сечения, называется рациональной осью. В поперечном

• сечении арки с достаточно вытянутой осью возникает только сжимающее нормальное напряжение. Уравнение рациональной оси трехшарнирной дуги получено из условия эквивалентности изгибающего момента нулю: =M2— / y / =0, где ug=M^N. При заданном типе внешней нагрузки и положении шарнира ось Н постоянна, а Осевая формула определяется законом изменения балочной диаграммы изгибающего момента и пытается определить Ариальную ось симметричной трехшарнирной арки, которая нагружена

вертикальной равномерной распределенной нагрузкой прочности Q по длине пролета. Средний шарнир расположен на расстоянии f от линии, соединяющей опору. Эталонная реакция: VB=Vc=qU2\n=qV4bf. V при изгибающем моменте балки=g в любом сечении на расстоянии z от левой опоры?z2 / 2=qlz / 2-qz^W, Затем y (g)=(qlz/2-qz/2)=4/(lz-z)/l*. Таким образом, при действии на трехкрылую дугу вертикальной равномерной распределенной нагрузки рациональная ось представляет собой вторичную параболу. Разумным контуром равномерно распределенного гидростатического давления (давления, перпендикулярного оси свода) является окружность

оси при действии на три шарнирные дуги. Под действием постоянных и временных Людмила Фирмаль

зависимости от сочетания этих нагрузок. В этом случае необходимо принять уравнение оси дуги таким образом, чтобы ось занимала среднее положение в диапазоне возможных отклонений кривой давления. Однако такое решение не всегда возможно, так как оно может привести к сложному уравнению оси арки, что затрудняет ее изготовление. На практике уравнение оси дуги обычно принимают за простую кривую. 331близкой на кривой среднего давления. С арками из материалов с низким конструктивным сопротивлением растяжению (бетон, кирпич и др.), появление растягивающих напряжений не допускается. В случае смещения центра сжатия

нормальное давление определяется по формуле: О2= — н/д±М/Ж х=-П/а±нэ/WX С где A-площадь поперечного сечения, WX с моментом сопротивления; е-эксцентриковые. Для прямоугольных секций высотой h и шириной b A=bh\Wx=bh2 / 6=Ali / 6, 1 часть каркаса в сборе должна быть шарнирной или эластичной, Затем oz= — N/a±6Ne / Ah= — N/A (±Ge / h). Для обеспечения того, чтобы поперечное сечение свода не испытывало растягивающего напряжения, требуется 1-6E/L=0 или e^/i/b.

Смотрите также:

Решение задач по технической механике

Аналитический расчет трехшарнирной арки	Статически определимые плоские рамы. Общие сведения.
Трехшарнирная арка с затяжкой	Аналитический расчет простых рам