Аналитический расчет трехшарнирной арки

Аналитический расчет трехшарнирной арки

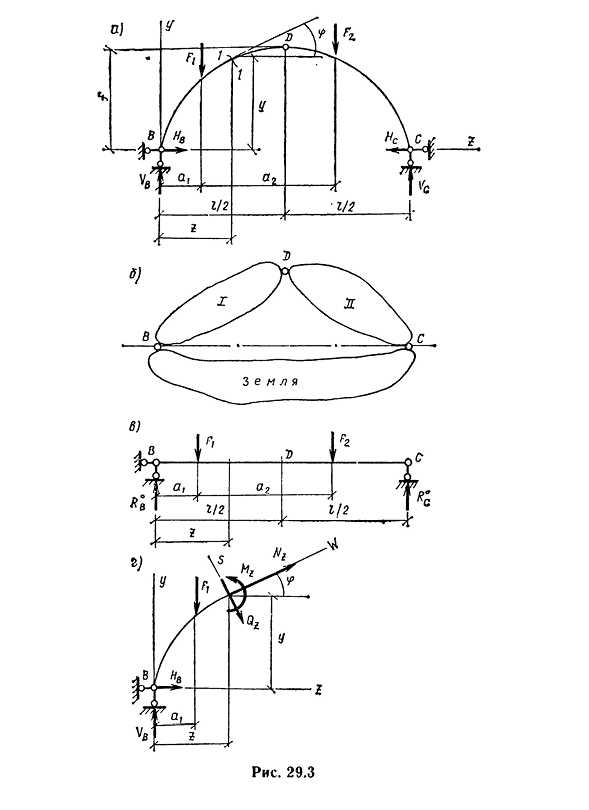
• Рассмотрим три шарнирные арки с опорой на одном уровне в пролете I и стрелу f, установленные с любой вертикальной нагрузкой(рис. 29.3, а). Уравнение оси дуги, называемой левой опорой начала координат, известно и Y= Где z-текущая координата любой точки на оси дуги. Средний шарнир D находится в середине пролета арки. Во-первых, мы проведем кинематический анализ. Трехшарнирная арка состоит из двух дисков BD и DC, Соединенных простым цилиндрическим шарниром в точке D и установленных на земле четырьмя опорными стержнями. Таким образом, степени свободы

117=3-2-2-1-4 = 0- 312!Рис. 29.3 кроме того, три шарнирные арки имеют необходимое количество соединений. При анализе геометрической структуры к двум дискам арки добавляют основание (грунт), представляющее собой неподвижный диск. Затем два диска свода вместе с третьим диском основания образуют геометрически неизменную и неподвижную систему, три диска шарнира B 29.3 B). Таким образом, три шарнирные арки являются неизменной, статически определимой системой. Поддержите решение реакции. Четыре реакции поддержки происходят в связи поддержки

трех дуг. Показаны вертикальная и горизонтальная составляющие Людмила Фирмаль

соответственно VB, VC, HB и HC(рис. 29.3, а). Для определения четырех стандартных реакций используются три уравнения статического равновесия для плоской системы сил. Помимо уравнений статики, существует полная система статических уравнений для определения четырех опорных реакций, которые создают уравнения, равные нулю изгибающего момента относительно промежуточного шарнира D от всех сил, расположенных слева или справа от этого шарнира.、 YMB=0; 2MS=0 (or=0); SZ=0; . EM » EV= = 0. В данный момент направленный по часовой стрелке, мы считаем положительным. Из первого уравнения находим эталонную реакцию Vc: =Форекс аль+Ф2(А2+а j-ВК=0,где 4-Ф2(А2 4-Аджи/з- Из второго уравнения

находим эталонную реакцию V B: SAfc=f D / — » J-F2 (/- a, — =0, Где VB=[F1(I-a j+F2 (I-a^\H. Полученные уравнения Vb и Vc показывают, что в дуге гречшарнира с вертикальной нагрузкой вертикальная реакция равна соответствующей ver- 319tical реакция такого же профессионального одиночного луча пяди? Лето от той же нагрузки(рис. 29.3, в): ^b=^b и — #C’где Rqb и является вертикальной опорной реакцией в одном спанболе * ke с совместной опорой. Из третьего уравнения мы узнаем =HB-NS = 0 , Здесь H b=N C=N, то есть горизонтальные опорные реакции в трехшарнирной дуге от вертикальной нагрузки равны между собой и направлены в противоположную сторону. Обычно они обозначаются одной буквой N. Значение горизонтальной опорной реакции определяется из

• четвертого уравнения: = — F+VB1 / 2-Fl (1/2-a j=0, Откуда он взялся Молекула полученной формулы представляет собой изгибающий момент в поперечном сечении D однопролетной балки, имеющей шарнирную опору того же пролета, что и арка, и нагруженной той же вертикальной нагрузкой.: Б. У з-ф^у З-^М Л. Тогда уравнение горизонтальной опорной реакции можно записать следующим образом: Ч= (29.1) Из полученного уравнения видно, что горизонтальная опорная реакция (рашпиль) прямо пропорциональна изгибающему моменту балки для поперечного сечения в соответствии с шарниром Z и обратно пропорциональна размерам стрелы дуги в промежуточном шарнире F. Определение коэффициента внутренней силы в сечении свода. Для определения коэффициента внутренней силы в арке используют метод сечений. Разрежьте арку на две части в 1 — / вертикальном сечении

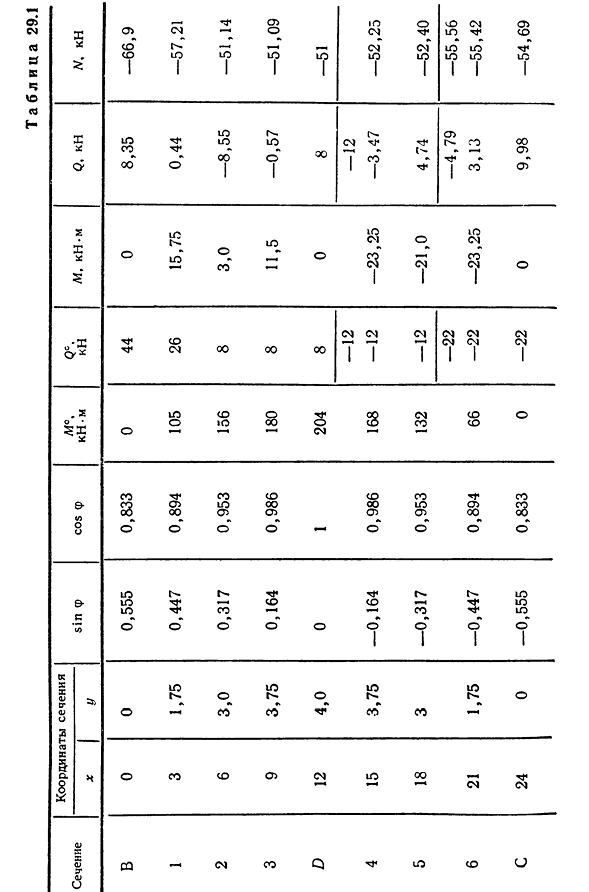
относительно ее оси, расположенной на любом расстоянии от левой опоры B (отбросьте правую часть, а тень слева уприте в 29.3 g). Горизонтальная ось 320обозначима через продольную-y ZT от центра сечения/-1, угол наклона касательной в контакте с осью свода этого сечения — — h sin 09 51 66.9 52.25 55.56 Да2 5Вт> Н(х) Рис 29.4 21 * 324 Т а б л и Ц А29. Один Раздел Координаты участка s в F COS f * 1Y В Ноль. 0 0.555 0.833 Один. 3 1.75 0.447 0.894 Два. 6,0 0,317 0,953 Три. 9 3,75 0,164 0,986 Д 12 4, 0, 0, 1. Четыре. 15 3,75 — 0,164 0,986 Пять. 18 3-0-317 0-953 Шесть. 21 1.75-0.447 0.894 На » S24 » 0-0. 555 0.833 м°, кН м Контроль качества. кН м, кН «м», кН м кн Ноль. Сорок четыре. 0 8,35-66,9 105 26 15.75 0.44-57.21 156 8 3,0-8,55-51,14 180 8 11.5-0.57-51.09 204 8 0 8-51 -12 -12 168 — 12 -23,25 -3,47 -52,25 132 —

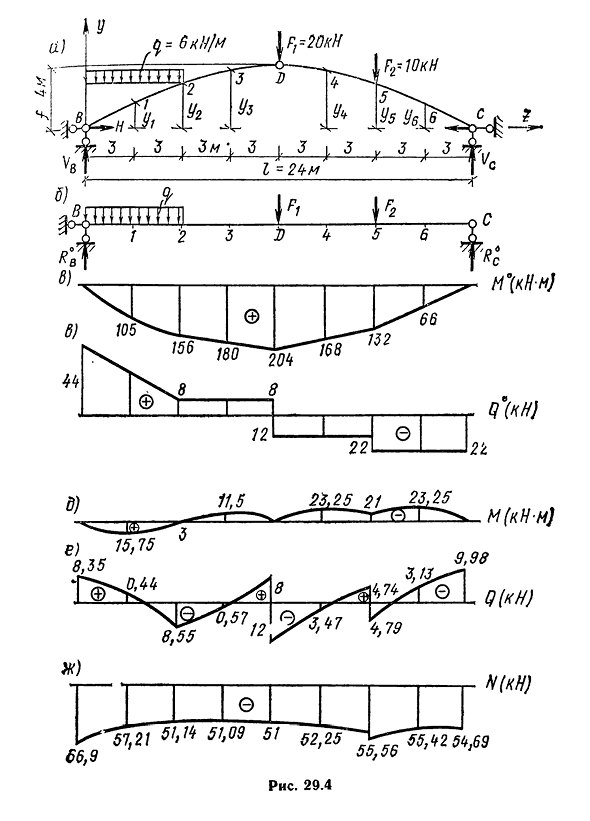
12 -21,0 4,74 -52,40 -22-4.79-55.56 66-22-23. 25 3.13-55.42 0-22 0 9.98-5 4,6 9 нагрузка нагрузки (рис. 29.4, а). Ось Людмила Фирмаль

дуги очерчена вторичной параболой y=4f (1G-2*) / 1\называется началом скола! На левой боковой опоре. Решение. Сначала находим значение вертикальной составляющей опорной реакции VB и Vc-24MV=(7-6-3+ / y12+ / y18-Vc-24=0; Vc= (6-6-3 + 20-12 + 10-18)/24 = 22 kN;BMS= — g-6-21 — / y12-F2-6+VB-24=0; VB= (6-6-21 + 20.12 + 10• 6)/24 = 44 кн. Проверим найденную вертикальную реакцию: SF=Vs-g-6-F1-F2+Us= 0, 44 — 6-6 — 20 — 10 + 22 = 0. Вертикальной опорной реакции был найден, чтобы быть правдой. Определим горизонтальную опорную реакцию JV и NS — при вертикальной нагрузке горизонтальная опорная реакция HB H N s равна друг другу и находится в противоположном направлении:h V=NS = H=H = M°D/f = y-q-6-9j/f=(44-12-6-6-6-9)/4= =51кн. Чтобы построить участок M, Q и N, мы разделяем арку на восемь равных частей длиной 3 м. 1,2, в фиксированном

разделе…Найти координату y по заданному уравнению оси дуги с; r/=4/(Zz-z2) / Z2 и тригонометрические значения по формуле: Y’=tg f=4///2 (I-2z); cos f=l/K b F t g4; sin f=cos f tg f. Так как коэффициенты внутренней силы L4, Q и N в своде представлены изгибающим моментом балки и поперечной силой балки Q^, то сначала определим их значения. Для этого замените арку на однопролетную балку того же пролета и нагрузите ее той же нагрузкой, что и арку(рис. 29.4, 6). Сюжет M®и появляется в Riis. 29.4, в, г. 1,2, в фиксированном разделе…. В изгибающем моменте арки боковые и вертикальные силы рассчитываются по следующей формуле(29.2), (29.3), (29.4). Результаты расчета этих величин представлены в таблице. 29.1 фигуры M, Q и N в арке показаны на рисунке. 29.4, д-У.

Смотрите также:

Решение задач по технической механике

Аналитический расчет многопролетных статически определимых балок	Трехшарнирная арка с затяжкой
Трехшарнирные арки. Общие сведения	Кривая давления. Рациональная ось арки