Пределы применимости формулы Эйлера

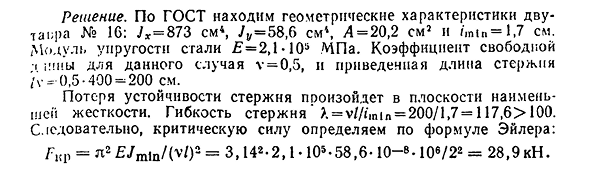
Пределы применимости формулы Эйлера

• Уравнение Эйлера выведено из дифференциального уравнения для криволинейной оси стержня. Поэтому его можно использовать до тех пор, пока напряжение в стержне не превысит предел пропорциональности материала. Соответствующая критическому

значению сжимающей силы 272, потеря устойчивости несжимаемого нормального напряжения в поперечном сечении называется критическим напряжением и равна: n CR=^CR/L=n2£V m in/(vl)2A, (21.5)где A-площадь поперечного сечения стержня. Геометрическая характеристика сечения ‘ K/minM== * min-

это величина минимального радиуса инерции сечения стержня. Выражение (24.5) Людмила Фирмаль

можно записать в виде: CR = L2£ / (V // Показать — — — -=%. Значение X называется гибким- ГЧП Как закрепить конец стержня, зависит от длины и жесткости поперечного сечения. Наконец, мы получаем следующее уравнение для критического напряжения: R to=l2£ / %2. (24.6) Поэтому можно использовать формулу Эйлера при определенных условиях.: Переменного тока Р=Л2£ / П2<п.С, (24.7)где

и.С-предел пропорциональности материала. Откуда он взялся K>n V (24.8), значение l V£/UCP.C=Apred называется предельной гибкостью и зависит только от физико-механических и прочностных свойств материала, а не от его размеров. Написав формулу гибкости(24.8), мы получаем условия применимости формулы Эйлера следующим образом Б>^предварительно(24.9) Таким образом, уравнение Эйлера

• применимо только в том случае, если гибкость расчетного стержня больше или равна конечной гибкости материала, из которого изготовлен стержень, например, стальной ОП мягкой структуры.Для C=200MPa и£ ‘ =2-105MPa^pre=3, 14V2-105/200=100. Поэтому для стержней из низкоуглеродистой стали формула Эйлера применима, если требуется гибкость- 18-480. 273,10. Аналогично получены

требования применимости формулы Эйлера для прутков, изготовленных из других материалов:для чугуна L pre=80, для молибденовой стали Hpred= = 70 и др. Для таких стержней критическое напряжение определяется эмпирической формулой Ясинского, полученной на основе большого числа экспериментов: 24.10) Здесь A и b-коэффициенты, зависящие от материала. Например, для низкоуглеродистых сталей со степенью изгиба, которая варьируется от 40 до 100, коэффициенты

а и в принимаются равными<2-310мпа и в * 1,14 МПа. При гибкости от 0 до 40 Людмила Фирмаль

критическое напряжение считается постоянным и равным пределу текучести материала. График зависимости критических напряжений от гибкости стержня из низкоуглеродистой стали показан на рисунке. 24.7, состоит из трех разделов. 1. Гибкость от 0 до 40 (низкий Полюс гибкости), имеет постоянное значение напряжения OCD. Стержень предназначен не для устойчивости, а для прочности o=N / A. рассчитано для 2. При гибкости от 40 до 100 (средние бары гибкости) зависимость от гибкости OCR линейна, они рассчитываются для устойчивости по формуле Ясинского OCR = o-B’C, 3. Для гибкого стержня больше 100 зависимость ОКР от гибкости гиперболическая, а

устойчивость вычисляется по уравнению Эйлера ОКР=L2E / x2. Например. Для двутавровой балки № 16 стальные стержни с жесткой опорой на конце длиной/=400 см нагружают центром сжимающей силы, рассчитывают величину критической силы L—. 274 разрешение по ГОСТу, выяснить геометрические характеристики двутавра № 16: Jx=873cm4, 7^=58. 6cm4, L=20. 2cm2 и / mtn=l, 7 см / модуль упругости стали = 2,1105 МПа. Коэффициент свободного d 1!!В этом случае v=0,5, а длина данного стержня/V-0,5-400=200 см. Потеря устойчивости стержня происходит в наименее жестких плоскостях. Гибкость стержня*X=v / / im in=200 / l>7=117,6>100. Таким образом, критическая сила определяется уравнением Эйлера: GK p=l2^Zmln / Cv/)2 = 3,142- 2 ,1 • 105-58,6-10—b-10B / 22=28,9 кн.

Смотрите также:

Решение задач по технической механике

Формула Эйлера	Практическая формула для расчета на устойчивость
Влияние способа закрепления концов стержня на критическую силу	Понятие о действии динамических нагрузок