Оглавление:





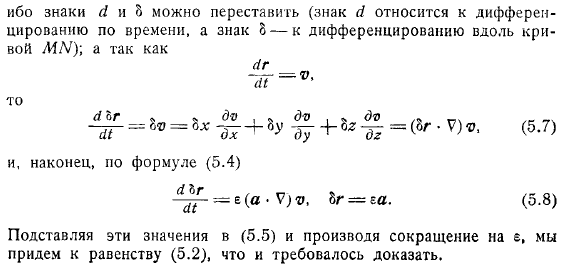



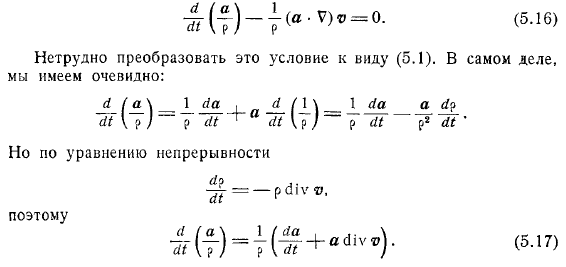



Сохраняемость векторных линий
Принимая во внимание важность теоремы Гельмгольца, которая только что была установлена, мы снова докажем их с помощью другого метода, начиная с дифференциальных уравнений вихря скорости. Но сначала нужно рассмотреть общий вопрос гидромеханики об условиях сохранения векторных линий. Предположим, существует некая движущаяся среда, и ее поле скоростей задается вектором, который, в общем случае, зависит от.
Кроме того, рассмотрим другие векторы, такие как вектор ускорения и вихрь скорости. Нарисуйте векторные линии вектора, то есть линии каждой точки, вектор направления которой a касается этой линии. Уравнение этих линий в векторной форме или декартовых координатах: вообще говоря, совершенно ясно, что в разных точках времени мы обычно получаем набор разных векторных линий теорем Гельмгольца. Если рассмотреть векторные линии, соответствующие моменту, то можно увидеть, что, в общем случае, она состоит из частиц среды, которые в данный момент принадлежат разным векторным линиям.
Но в некоторых случаях возможно, что частицы среды составляют момент. На данный момент векторные линии также образуют векторные линии. Если эта последняя ситуация применима к векторным линиям в любой данный момент и заданному вектору, то это говорит о том, что векторные линии a имеют характер сохранения. Если векторные линии вектора имеют характеристики сохранения, то каждая векторная трубка остается векторной трубкой на протяжении всей продолжительности непрерывного движения среды.
Это связано с тем, что он ограничен набором векторных линий. Однако и в этом случае можно выделить подвида. Первый подслучай — это когда сила вектора трубы-площадь поперечного сечения трубы изменяется с течением времени. Подслучай — это когда сила векторной трубки остается постоянной на всем протяжении. В этом последнем случае мы говорим, что сила векторной трубки имеет свойство. В приведенном выше векторном примере сила векторных линий и векторных трубок обладает свойством постоянства.
То есть, согласно теореме Гельмгольца, которая была доказана выше, такой вектор является вихрем скорости при любом движении идеальной баротропной жидкости, находящейся под действием потенциальных сил. Далее, в рассматриваемой области будем считать, что векторы непрерывны с их частными производными, а величина вектора a не равна нулю. Тогда только векторная линия проходит через каждую точку в интересующей области. А.А.Фридман.
Докажите следующую ведущую теорему, принадлежащую теореме. Необходимое и достаточное условие как для векторной линии вектора, так и для прочности сохраненной векторной трубки заключается в реализации уравнения — во всей рассматриваемой области всех учтенных моментов мы делим доказательство этой теоремы на части. Во-первых, покажем, что условие, необходимое для сохранения векторной линии вектора, состоит в том, что равенство.
Фактически, пусть мы будем векторной линией времени частицы жидкости, образовавшей линию в момент времени в этом случае точка переместится в точку, а точка, бесконечно близкая к, будет. Предположение, линия является векторной линией в данный момент, поэтому вектор касается линии точек. Введение обозначения дает понять, что векторные линии присутствуют, а затем это бесконечно малое число скаляров.
Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке. Людмила Фирмаль
Условие наличия векторной линии описывается точно следующим образом: или. Первый член слева равен нулю в силу, и последний член может быть отброшен как более высокая минимальная величина, чем другой. Если вы разделите оставшиеся условия, вы получите условие. Так как символ можно переставить уравнения Фридмана Гельмгольца (символ относится к производной по времени, а символ o относится к производной по кривой), то в конце, подставляя эти значения для них и уменьшая их, они при необходимости будут равны.
Здесь векторная линия вектора a не только сохраняется, но и указывает на то, что векторная сила трубки равна требованию. Доказательство продолжается точно так же. Необходимо только учитывать дополнительные условия для сохранения прочности векторной трубки. Подумайте о бесконечно тонкой векторной трубке. Его прочность равна, где площадь поперечного сечения трубки в точке. После периода векторная трубка занимает новое положение, и существует выражение для ее прочности.
Где площадь поперечного сечения трубки в точке. Для каждого условия новое положение должно использовать условие, что векторная трубка заполнена теми же частицами, что и исходное положение. Масса бесконечно малого цилиндра с длиной поперечного сечения трубы и длиной дна, вырезанного из вихревой трубы, равна. Где плотность среды в некоторой точке. Указанный минутный объем переходит в цилиндрический объем трубки, его поперечное сечение равно, ребро, масса, плотность в момент точки. Масса этих томов должна быть одинаковой, так оно и будет.
Если сравнить эту эквивалентность, то для краткости можно ввести новый вектор и переписать его в том виде, в котором указана сумма значений предыдущих соотношений. Однако мы знаем, что направления векторов одинаковы, поэтому имеет место не только уравнение скаляра, но и вектор. Равенство, это последнее отношение упрощается: применяя формулу, оно выглядит так: наконец, используя и уменьшая, мы получаем: таким образом, мы нашли искомое условие в следующем виде: это условие можно легко преобразовать в. Факт, это понятно.
Но, согласно уравнению неразрывности, таким образом, подставляя это значение в уравнение и уменьшая его, мы достигаем необходимого. Это полностью эквивалентно равенству. Наконец, это указывает на то, что предыдущее условие является достаточным для сохранения a в качестве векторной линии. И сила векторной трубки. Создайте векторную линию вектора в начальный момент времени. Теперь для любого момента построим поле вектора следующим образом: возьмем любую точку и в момент проведем векторную линию.
Когда частицы жидкости, составляющие эту векторную линию, образовали жидкую линию в момент времени, и точка переместилась в точку, вектор был направлен в точку по касательной линии в момент времени, и вектор также хранил бесконечно малый вектор, сила которого охватывала линии. Построенный вектор имеет характеристики непрерывности векторных линий и взаимодействия векторных трубок, поэтому он должен удовлетворять соотношению при.
Далее, по гипотезе, вектор также удовлетворяет уравнению. Но дифференциальное уравнение, линейное по отношению к, имеет свое собственное решение, которое в первый момент принимает определенное начальное значение. Поэтому вектор должен соответствовать вектору. Следовательно, вектор и векторные трубки должны обладать свойствами сохранения прочности векторной трубки.
Поэтому упомянутые нами теоремы теперь полностью доказаны. Из-за важности вектора слева от уравнения Фридман ввел специальные названия и обозначения. То есть этот вектор называется полным Гельмгольцем вектора и обозначается как руль вектора. Поэтому необходимым и достаточным условием сохранения векторной линии вектора а и прочности векторной трубки является исчезновение руля этого вектора.
Например, вектор скорости ветра в данный момент времени различен в разных точках и может быть описан векторным полем. Людмила Фирмаль

