Оглавление:








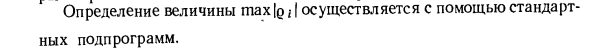

Количественные критерии оценки устойчивости по нормам и по следу матрицы В
- Количественные критерии оценки стабильности по стандартам и трассам матрицы B Исходя из вышеизложенного, можно определить, находится ли собственное значение Kf исходной матрицы коэффициента A на левой стороне мнимой оси комплексной плоскости X, просто подняв преобразованную матрицу коэффициента B до степени. Коэффициент в некоторой степени собственное значение р? Уменьшает абсолютное значение. Для всех p он находится внутри единичного круга и по модулю меньше единицы. Возникает вопрос: можно ли установить факты стабильности без поднятия матрицы B к степени? Последняя ситуация очень важна, поскольку она позволяет избежать громоздкой операции умножения матриц, тем самым сокращая требуемое машинное время.
Если это невозможно, важно знать, сколько раз матрица B поднимается. Рассмотрим возможность оценки распределения собственных значений для единичного круга с центром в начале координат согласно норме матрицы B. Напомним, что норма квадратной матрицы B вещественная ||. (| Условия: а) Только для || с ||> 0 и || с || = 0, B = 0. б) || cb || = | и | • || с || (c — число), особенно || с || = [| -с ||; в) || B + D || <|| || + || D ||; г) || БД || || В || • || D || Где B и D — матрицы, для которых имеет смысл соответствующая операция. В частности, для квадратных матриц || B * || << || B || , где k — натуральное число.
Рассмотрим следующую легко вычисляемую норму: N II B || t = max <6-24) 1 / -I N II BII ,, = Макс. V \ b \, (6,25) ( / II B ||, v = n max \ bi} . (6,27) Я Людмила Фирмаль
Чтобы система (6.2) была асимптотически устойчивой, а B * 0 — k-> oo, достаточно, чтобы одна из норм матрицы B была меньше 1. II B C <1. (6,28) В самом деле, согласно определению нормы (см. Условие d) II B * || C || В * «1 и • и в || <••• <• II CC *. Следовательно, || B || <1, тогда || B || * 0, поэтому B ° — »- 0 — это k ° по мере необходимости. Таким образом, для того, чтобы исследуемая система (6.2) была устойчивой, достаточно, чтобы любая норма была меньше 1, то есть выполнено условие: min (|| B || ,, II B || n, l | B || m, || B || 1V) <1. (6.29) Если условие (6.29) не выполняется, это не означает, что точка в пространстве параметров системы является нестабильной. Вопрос устойчивости должен быть дополнительно исследован с учетом порядка матрицы VA.
Убедитесь, что все собственные значения матрицы B находятся внутри единичной окружности с центром в начале координат (| qj | <1, i = 1, 2, n) и что все нормы матрицы B больше 1. Рассмотрим последовательность градусов B2, B4, B8, …, B2 «1; k = 2». Поскольку все собственные значения Jq * | <1, элементы матрицы B * стремятся начать с k и перейти к нулю при k oo. Тогда в несколько шагов || VL || <1. Это условие необходимо и достаточно для определения стабильности системы. Следовательно, стандартная оценка устойчивости выполняется в следующем порядке: 1. Матрица B создается из исходной матрицы системных коэффициентов A (6.4). 2. Рассчитывается одна из норм матрицы B или выполняется условие (6.29). Когда || B || <1, целевая точка пространства параметров принадлежит стабильной области. 3.
- Если соотношение (6.29) не выполняется, матрица B должна быть увеличена, и норма последовательных заказов должна быть принята во внимание. II B2 II, II B4 II, II B * II ….. II c * (I. Для любого фиксированного k, если любая из норм равна единице || B * || <1, то условие устойчивости B * -> 0 (k ° °) выполняется, и это является комбинацией этих параметров. Система считается стабильной. Пример 6.3. Рассмотрим преобразованную матрицу с коэффициентом B в примере (6.1) G — 0,21792 — 0,82742 — 0,586381 B = -0,11957 0,49C57-0,39177. L -0,28302 -0,03561 0,49820j
Определяет норму матрицы B N || CC, = максимум V | B1} | = максимум (0,21792+ 0,82742+ 0,58638; 0,11957 + 0,49057+ + 0,39177; 0,28302 + 0,03561 + 0,49820J = максимум (1,63172; 1,00191; 0,81683] = = 1,63172. N II B |||, Макс. Y I bif I = Макс. 10,21792 + 0,11957 + 0,28302; 0,82742 +0,49057 + «Я» + 0,03561; 0,58638 + 0,39177 + 0,49820J = макс (0,62051; 1,3536; 1,47635) = 1,47635. II II ,, =) / 0,21792- + 0,82742- + 0,58638- + 0,11957- + 0,49057? + -> + 0,391772 + 0,28302- + 0,03561- + 0,49820- ‘= V0,047489 + 0,6846238 + 0,34384 + 0,0142970 +0,2406589 + +0,1 534837 + 0, 0801003 + 0,001268 + 0,24882032 = K 1,8139639 = 1,334683.
При рассмотрении любого критерия выполняется достаточное условие, т. Е. Мил) (IIВ ||, ОС || ,,; || В | [ш) = (1.63172; 1.47635; 1.34683)> 1. Людмила Фирмаль
Степенная матрица B 0,31238-0,204712 0,15981] B * = | 0,07828 0,35354-0,31726. 07506 0,19896 0,42811J Матричная норма || B21 | j меньше 1, что указывает на то, что k oo удовлетворяет условию B * 0. |) B2 || j = max [0,676902; 0,74908; 0,69773) = 0,74908 <1. Рассмотрим возможность оценки собственных значений матрицы B позже. Известно, что непрерывный след степени матрицы B * является суммой всех собственных значений Qg * t, взятых в той же степени, что и матрица BA. SpB * = p * + p * + … = 2 пГ Если система стабильна и VL 0, след SpB * также стремится к нулю при k °.
Если рассматриваемая комбинация пространственных точечных параметров достаточно далека от границы устойчивости, матрица B не может быть возведена в степень, а является достаточным критерием неустойчивости. | SpB |> / i. (6,30) Если (6.30) выполнено, условие | q, |> 1 в jp ^ l. Фактически, предположим, что все | q / | <1. N G o ;; = o, (L-o, < 2 (6,31) / = я Неравенства в зависимости от условий N > стр. (6,32) 2 * Spb | = час Из справедливости неравенства 12. Из Р «1 <2 Вт» и (6.31) <«- | I-l Удар 2 * / = я (6,33) <Р. Противоречие между неравенствами (6.32) и (6.33) означает выполнение условия (6.30).
Следовательно, достаточно создать матрицу B, и если след абсолютного значения превышает порядок матрицы n, точка исследования пространства параметров не принадлежит области устойчивости. При поиске границ домена вы можете перейти к следующей пространственной точке, не поднимая матрицу B до степени. Если соотношение (6.39) не соблюдается, нельзя сделать вывод относительно отнесения исследуемой точки к нестабильной области. В этом случае можно рассмотреть поведение ряда трасс в матрице B \. | SpB2 |; | SpB4 |; …; | SpBA]. (6,34)
Начиная с некоторого k, отслеживаемая точка пространства параметров считается устойчивой, поскольку след трех последовательных порядков матрицы B * = B2, n уменьшается. Если матрица B повышается и результирующие порядки умножаются друг на друга (k = 2 «1), если все | q / | <1, аннулирование отдельных элементов матрицы приведет к разгрузке сетки машины. Таким образом, расследование может выполнить проверку на нулевой машине. Может быть предложен более точный метод оценки распределения собственных значений матрицы B относительно единичного круга. Удобным способом с вычислительной точки зрения является определение максимального по модулю собственного значения преобразованной матрицы с коэффициентом B.
Абсолютное максимальное собственное значение Максимальное число | q / | матрица B является решающим для оценки i Стабильность. Исходная система имеет все собственные значения Qt | qj | <1 матрицы B. Если максимальное собственное значение по модулю матрицы B превышает границу единичного круга, то есть, если максимум IqjI> 1, то между собственными значениями Из исходного матричного числа Kt с коэффициентом A справа от мнимой оси есть единица. Если значение max | qj | = 1, это соответствует устойчивой границе 1
Метод оценки устойчивости путем вычисления максимального по модулю собственного значения преобразованной матрицы с коэффициентом B является итеративным и, как и все итерационные методы, часто сходится медленно и увеличивает количество операций. Процесс решения проблемы длительный. Преимущества включают невозможность накапливать ошибки округления, которые ограничены только последней операцией. Определить значение | max | q | Реализовано с помощью стандартных процедур.
Смотрите также:
Примеры решения задач по теории автоматического управления

