Оглавление:










Влияние отсутствия в уравнении переменной, которая должна быть включена
- Эффект отсутствия переменных в уравнении, Должен быть включен Проблема смещения Предположим, что переменная y зависит от двух переменных x и x2 соответственно. По соотношению: ^ = a + p lxI + p 2×2 + w, (6.1) Тем не менее, я не знаю важность х2. Я считаю, что модель должна быть видимой как q> = a + p, x, +, n (6.2)
- Вы оцениваете регрессию j> = <7 + V i (6,3) рассчитать б X не по правильному выражению, а по выражению Cov (x ,, ^) / Var (x,) Формула дается формулой (5.12). По определению b {нет смещения Оценка 0, если E (LX) равно P. На самом деле, соотношение (6.1) верно Сначала интуитивное объяснение этого, а затем Министерство финансов.
В разделе 5.2, если x2 опущен в отношении регрессии, Переменная х {играет двойную роль: отражает прямое воздействие, Заменить переменную x2 в описании ее воздействия. Людмила Фирмаль
Это на первый взгляд косвенно Влияние х на у зависит от двух факторов: Имитирует способность x, поведение x2 и влияние x2 на y. Кажущаяся способность переменной x, которая объясняет поведение x2, определяется. Коэффициент наклона h псевдорегрессии. x2 = g + hxv (6,5) Значение A, конечно, рассчитывается по следующей нормальной формуле Парная регрессия, в данном случае Cov (x ,, x2) / Var (x,).
Влияние количества 2 у определяется коэффициентом р2. Поэтому эффект промежуточной имитации Значение p2 может быть записано как P2Cov (x ,, x2) / Var (x,). Прямое воздействие Размер более> описан с помощью пр. Зависимость регрессии}> переменная Xj (не включая Переменная х2) Коэффициент при х определяется по формуле: P, + P2Cov (x ,, x2) / Var (x,) + ошибка выборки. (6.6)
Ожидаемое значение, если х не является стохастическим Коэффициент представляет собой сумму первых двух членов этой формулы. Presents Второе слагаемое — математическое ожидание коэффициентов Процент отличается от истинного значения р, то есть оценочного значения Смещение применяется. Эффект х \ v \ Внешний вид \ значение xv \ Активный \ как альтернатива х2 • # Рисунок 6.1
Формальное доказательство соотношения (6.4) несложно. выполнение Серия теоретических преобразований оценки bx \ = Корова (x1? .Y) = CovCxjJa + Pi ^ + P2 * 2 + C]) = 1 Var (x!) Var (* i) [Cov (xi, a) + Cov (xj, Pi ^!) + Cov (xj, p2x2) + Cov (xj, u) = Var (x,) 1 Var (x,) [0 + p, Var (x!) + P2COU (X ,, x2) + Cov (x ,, u)] = ~ P l + P2 VarCx,) + Var (* i) ‘(6 л) Когда величины х и х2 нестохастические, при расчете Ожидаемое значение по теме для величины bx, которая является первыми двумя членами уравнения (6.7)
Он остается постоянным, а третий равен нулю. Отсюда Мулу (6.4). Это делает б { Ну, равно (i2Cov (x ,, Jc,) / Var (x,), направление смещения зависит от знака Количество р2 и COV (X, JC2). Например, если P2 положительный, Если ковариация идеальна, то смещение положительное, а bx — среднее Дайте переоцененный балл Случай. Однако есть один исключительный случай, когда оценка b {остается Это было предвзято.
Это происходит, когда выборочные ковариации xx и x2 точно совпадают ности ноль. Когда Cov (*, x2) = 0, смещение исчезает. эффективным Тем не менее, коэффициенты, полученные с использованием парной регрессии Точно так же, как правильно указанный рейтинг Регрессия. Конечно, значение смещения здесь будет равно нулю И p2 = 0, но в этом случае нет неправильной спецификации.
Неспособность применять статистические тесты Еще одно серьезное последствие не включения переменной Факт должен существовать в регрессии и формула для Стандартный коэффициент ошибок и тестовая статистика, как правило, 100 Не применимо Это, конечно, Как правило, получают результаты оценки регрессии Гипотезы. Монте-Карло базовая иллюстрация Объясните анализ с помощью экспериментов.
Это одна из разновидностей метода Монте-Карло, которую иногда считают Случай 5.4. Доход страны Тренировка (5), индекс интеллекта (IQ) и степень успеха. Для того, чтобы осы 10000 новых доходов добавляются каждый год на 1500 250 для минимум 10 лет обучения и IQ более 85. Кроме того, есть факторы удачи: у = 10000 + 1500 (5-10) + 250 (70 -85) + и. (6.8) Для упрощения это уравнение выглядит так: y = -26250+ 15005+ 250IQ + U (6,9)
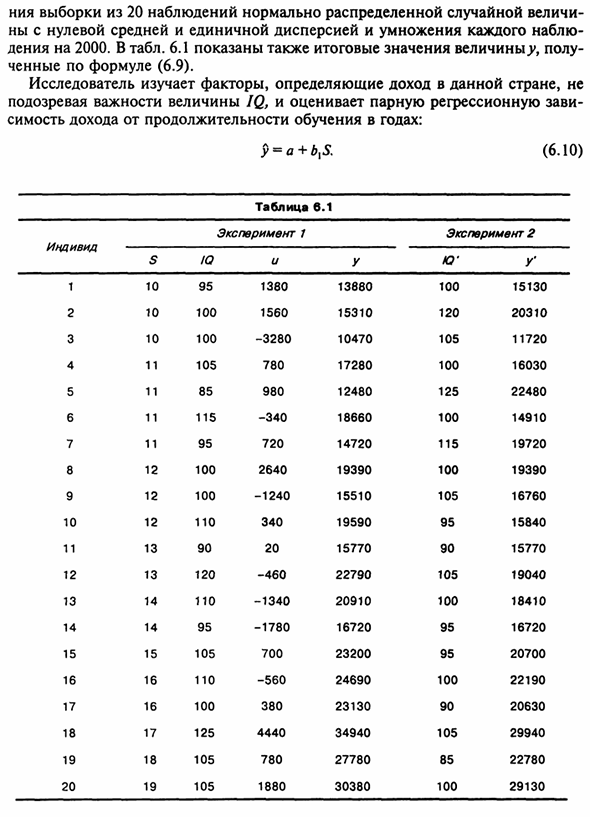
Первые три столбца таблицы. 6.1 Представление данных для мнимых выборов 20 человек заботятся. Значения S и IQ выбираются произвольно, но в результате Положительная корреляция. Положительная корреляция этих значений Одна из причин наблюдается во многих странах Распределение (однако Только) студенты с отличными способностями чаще бывают Провести конкурсные тесты для определения допуска к профессионалам Правильное образование.
Значения и были определены путем выборки из 20 наблюдений нормально распределенной случайной величины. Умножьте каждое на среднее, а единичная дисперсия равна нулю. Дения в 2000 году. В таблице. 6.1 также показывает общую стоимость ^ и полу Рассчитано по формуле (6.9).
Исследователи не являются фактором, определяющим доход конкретной страны, Подозреваю важность значения IQ и оценим коэффициент регрессии пары Годы дохода в течение периода обучения: Исследователи получают результаты: £ = -641 8 + 19855; II2 = 0,78. (6,11) (Co.) (3349) (248) К сожалению для исследователей, значения Sn IQ коррелируют. Для этого Пример формулы Cov (S, / 0 / Var (5) составляет 1,29. E (bx) = p! + p 2 ^ ^ ^> = 1500 + 250×1,29 = 1823 (6,12) Исследователи не включили IQ в уравнение, Коэффициент 5 имеет положительное смещение 323.
Конечно же Итоговая оценка может быть 1823, но она просто соответствует Когда показатель удачи равен нулю. Мы видим это Исследователь получил немного более высокий балл, который фактически равен 1985. Разница объясняется влиянием оставшегося члена в этой выборке. Если исследователь включает переменную IQ в уравнение регрессии, Результат оценки того же образца следующий. р = -29 586+ 16405+ 268/0; R2 = 0,93. (6,13) (4155) (151) (43)
Оценки коэффициентов, полученные исследователями, объективны И по крайней мере в этом случае практически близка к их истине Значение. Очевидно, что уравнение регрессии получено исследователем Уравнения составлены с правильными спецификациями, зависимостями Взятый из фактического значения случайного члена в выборке, это не будет правдой Здорово придать вес одному эксперименту.
Предсказуемые результаты. Проверено в соответствии с этим экспериментом Отказался еще 9 раз, используя одинаковые значения S и IQ в каждом Соблюдайте те же значения для был, р и р2, но разные наборы Случайная реализация остаточного члена. Соответствующие результаты регрессионной оценки приведены в обобщенном виде 6.2 на столе. Из этой таблицы видно, что полученные результаты подтверждены. Жду предыдущих выводов.
Исследователь получает оценки коэффициента S, перемещенных 1823 (те из них Его значение составляет 1854). Если спецификация верна, оценки разбросаны Вокруг истинного значения 1500. То же самое утверждение может быть сделано Лан для постоянного члена уравнения. А что будет, если исследователи не включат вместо IQ? Что такое переменная S в уравнении регрессии?
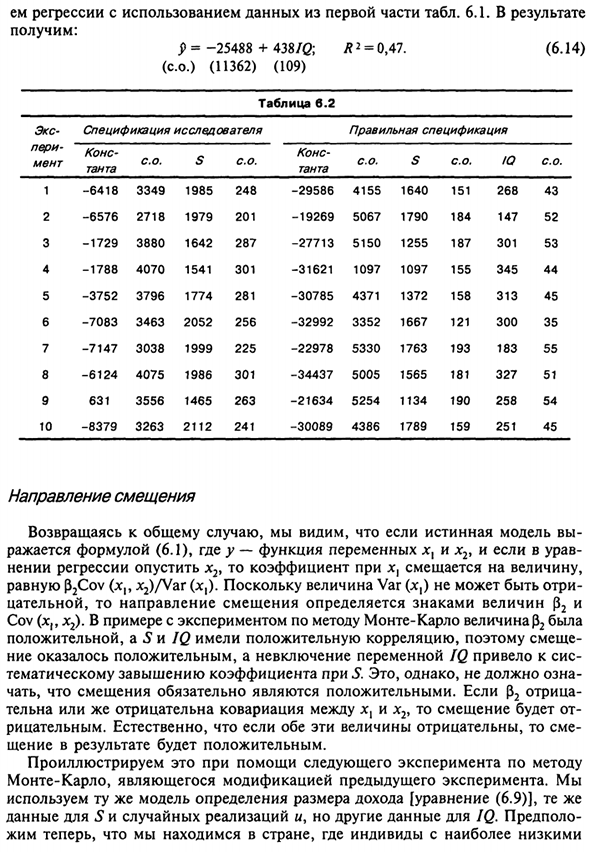
В этом случае значение IQ частично Выступал в качестве переменной, некоторые в качестве альтернативы Носитель отсутствующей переменной S. Повторите приведенный выше анализ Потому что коэффициент P, Cov (5, / Q) / Var (IQ). р = 1500 и Cov (S, / 0 / Var (IQ) = 0,104, т. Коэффициент сдвинут вверх на величину, равную 156 и его матовая Ожидаемое значение 406. Этот вывод 170 Регресс, используя данные из первой части таблицы. 6.1.
В результате Мы получаем: 9 = -25488 + 438 / Q; D2 = 0,47. (6,14) (S.) (11362) (109) Направление смещения Возвращаясь к общему случаю, истинная модель Это выражается уравнением (6.1). Где у — функция переменных х и х2, Если регрессия x2 опущена, коэффициенты x сдвигаются следующим образом: Он равен p2Cov (x ,, x2) / Var (x,). Поскольку величина Var (x,) не может быть отрицательной Для твердых тел направление смещения равно величине p2 и Ков (xf, x2).
- В примере Монте-Карло значение P2 Потому что это было положительным и была положительная корреляция между 5 и IQ. Это оказалось положительным, и невключение переменной IQ привело к системе Завышение предмета по коэффициенту в с. Тем не менее, это Обратите внимание, что уклон всегда положительный. Если (52 негатива Если ковариация x и x2 отрицательна или отрицательна, смещение.
Осторожно. Конечно, если оба эти значения являются отрицательными, Результат положительный. Это модификация предыдущего эксперимента. мы Используйте ту же модель, чтобы определить сумму дохода [Уравнение (6.9)], то же S данные и случайная реализация k, но IQ другие данные. вероятно.
Следующий эксперимент с этим методом проиллюстрирует это Монте-Карло Людмила Фирмаль
Теперь подтолкнуть нас, чтобы быть в стране с самым низким человеком 171 Способность, определяемая значением IQ, проходит самый длинный Обучение для достижения того же уровня образования, что и все. но Данные Значение IQ, показанное как IQ, приведено во второй части Tab. 6.1. Эта таблица показывает, что значения S и IQ имеют отрицательную корреляцию Ван.
6.3 показывает результаты оценки регрессии. Регрессия (указана правильно) и двухпарная регрессия (неверно) Было указано). Коэффициенты регрессии пары S и IQ’B значимы Значительно ниже соответствующих нескольких рег ressii. Сдвиг коэффициента регрессии, когда переменная IQ опущена Если S равно P2Cov (S, / 0) / Var (S) = 250 * (-1,80) = -450 Когда переменная S включена, коэффициент сдвига в IQ равен ‘ P, Cov (£, / QVVar (IQ ‘) = 1500x (-0,145) = -217.
Очевидно, результат Регрессионные оценки подтверждают выводы. Согласно интуитивному объяснению, согласно этой модели Люди с длительными периодами исследования относительно Высокий доход, но в то же время они обычно имеют более низкий IQ Уменьшите их доход. В результате регрессионная зависимость пары Конечно из-за периода обучения Это верно.
Точно так же индивидуумы с высоким IQ являются относительными Относительно высокий доход, но в то же время в принципе они относительно Преимущества уменьшены, потому что период обучения очень короткий. Отсюда на пару Нет регрессионной зависимости дохода от значений IQ. Эффект IQ недооценен Nitcha. Иногда этот уклон достаточно силен, чтобы заставить Символ изменения коэффициента регрессии.
В рассматриваемом режиме Был ли истинный коэффициент в IQ 25 вместо 250. Как и раньше, получаем сдвиг коэффициента в данных S и IQ \ IQ ‘, Равен -217, если переменная разрешена. Поэтому математические ожидания Коэффициент IQ \ 25 = 217 = -192, положительный 100 Это не отрицательно. В таблице. 6.4 Представление результатов оценки правила Но неправильно указана регрессия.
В третьей регрессии коэффициенты 172 Коэффициент IQ действительно отрицательный (–171). (Это немного большой Вместо математических ожиданий расхождения здесь Модель случайных членов. ) Операция фактора невключения R2 Пояснительная переменная В разделе 5.6 множественный регрессионный анализ Вы можете определить вклад каждой объясняющей переменной в коэффициенты В L2 я объясню, почему это так.
Во-первых, Метод Монте-Карло «Доход — Обучение — Интеллект», Период обучения Существует положительная корреляция между значением и IQ. Когда мы увидели это Значение регрессионной зависимости значения Y только для значения S, значение Значение коэффициента R2 составило 0,78. При оценке регрессии Зависимость K только от значения IQ, значение коэффициента R2 0,47.
Означает ли это, что значение S составляет 78% дисперсии дохода? IQ составляет 47%? Конечно нет Объясняет 125% дисперсии, но это невозможно. На самом деле их суставы Стабильная объяснительная способность, часто выражаемая фактором L2 Естественная регрессия [Формула (6.13)] составляет 0,93. Объяснение это доход и Когда дело доходит до обучения, значение S играет свою роль, Используйте вместо отсутствующей переменной IQ (рисунок 6.1).
Следовательно, коэффициент Процент этой регрессии /? 2 отражает общую объяснительную способность Обе эти роли маскируют 5, а не способность прямого объяснения Переменная S. Поэтому значение 0,78 является переоценкой последнего. Точно так же переменная IQ для парной регрессии между доходом и метриками IQ интеллект частично заменяет отсутствующие переменные S и URO Степень регрессионного коэффициента R2 отражает общее объяснение.
173 Значение IQ в обеих этих ролях Свойство самого значения IQ. В этом эксперименте Монте-Карло уровень коэффициента равен R2. Наблюдается простым увеличением регрессии за счет альтернативных эффектов Ния. В эксперименте Монте-Карло, результат Tab. 6.3, происходит обратное. В этом эксперименте отрицательный Корреляция S и IQ ». В результате Парные регрессионные переменные были консервативно смещены.
Их очевидная ответственность также была нарушена. переменная S объяснил только 55% дисперсии выручки и объяснил только IQ ‘-1%. так Вместе они составляли только 56% дисперсии. В то же время коэффициент Введите R2 с правильно заданными множественными регрессионными показами Их совместная ответственность на самом деле составляет 89%.
В парной регрессии между доходом и / 0 этот эффект особенно Это так остро, что это больно. Деструктивный эффект из-за отсутствия переменной S в функции Почти уравновешивает прямое влияние переменной IQ и, следовательно, коэффициент Регрессия CNT Очевидно, лишь малая часть истинного значения Способность к четкому объяснению, которая была незначительной 1%, явно Он отказался.
Таблица 6.4 показывает разные результаты. Нормальный. Опять же, существует отрицательная корреляция между S и IQ \ Однако истинный коэффициент переменной IQ равен 25 Вместо предыдущих 250. На самом деле, значение S было «ответственность». Большая часть дисперсии дохода, а также уровень коэффициента регрессии пары L2 Значение между S и S почти так же высоко, как коэффициент Регрессия.
Регресс выручки и IQ Эффект демпфирования из-за отсутствия переменной S доминирует над прямым эффектом IQ ‘. В результате последний отклоняется Коэффициент с достаточно высоким значением коэффициента R2 Значение этого R2 в основном является переменной IQ1 Действует в качестве замены отсутствующей переменной S. упражнения 6.1.
Предполагая множественную регрессию [Уравнение (5.3)] между расами Еда (y), располагаемый личный доход (x) и относительное движение Определяет направление смещения, если цена (p) указана правильно Коэффициент другой переменной (если не включен): 1) Переменная p И 2) переменная х. Используйте относительную цену еды Поскольку эффект в течение периода выборки несколько увеличился, p и х имеет положительную корреляцию.
В таблице приведены результаты оценки. Множественная регрессия и парная регрессия: прокомментируйте разницу в коэффициентах трех указанных уравнений. 6.3. В упражнении 2.4 вы создали парную регрессию расходов и расходов Тип пособия (y) и располагаемый личный доход (x), а также во время учений Вариант 5.3-
Множественная регрессия между количеством j>, хир-стоимость Кроме того, по сравнению с общей инфляцией. Постройте парилку сейчас Только регрессия между значением y и показателем p. Отправить результаты Из этих трех регрессий Упражнение 6.1 и Изменение коэффициента при x и /> и изменение уровня коэффициента Энтера L2.
В частности, указать направление ожидаемого смещения С той же регрессией, с правильными множественными спецификациями, Примите во внимание тенденции области (если есть) Носимая цена и использование в течение того же периода, что и упражнение 5.1 Формула (6.4) 6.4. Повторите упражнение 6.3, используя логарифмическую функцию.
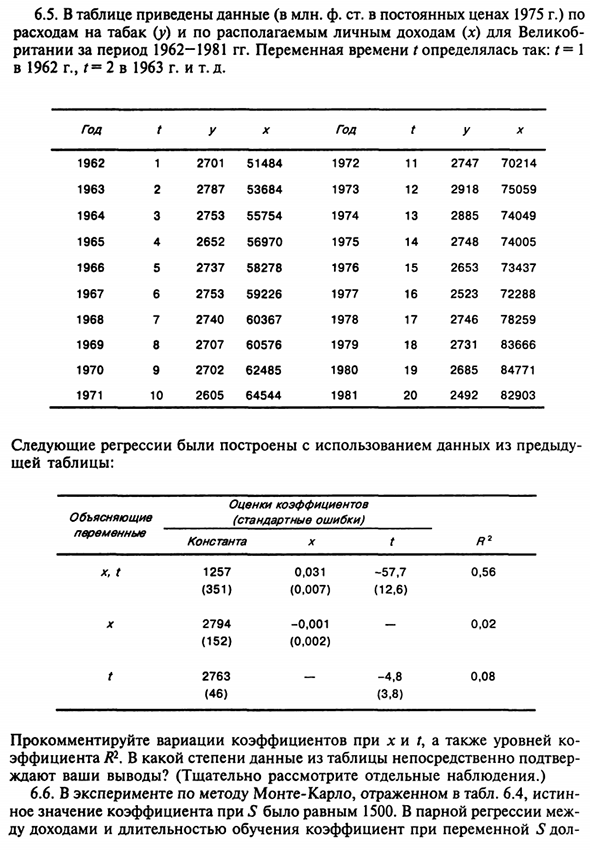
Са, не линейный. 175 6,5. В таблице приведены данные для миллионов фунтов стерлингов по прейскуранту 1975 года. Расходы на табак Velikob (у) и располагаемый личный доход (х) Переменная времени Ритании t с 1962 по 1981 год определялась следующим образом: f = 1 В 1962 и 1963 гг. F = 2 и т. Д. коэффициент вариации при х и /, Фактор R2.
В какой степени данные в таблице проверяются напрямую? Ты ждешь заключения? (Пожалуйста, внимательно проверьте каждое наблюдение.) 6.6. В эксперименте по методу Монте-Карло это отражено в таблице. 6.4 Верно Коэффициент для S был 1500. Доход и период обучения, переменный коэффициент S доллара 176 Беспристрастные жены.
Что вы думаете о фактическом предполагаемом весе? Маска, которая превышает истинное значение (1618)? 6.7. В эксперименте Монте-Карло, описанном в разделе 5.4, Дохо Год (Y) — период обучения (S), опыт работы (X) и Ластом (A). Значения ChiA имеют положительную корреляцию, S — Отрицательная корреляция с каждым из них.
Внизу слева В таблице показан уровень коэффициента L2 при оценке зависимости Мост: 1) только значение S 2) Из значений S и X. 3) Из значений S и Кай А В правой части таблицы показан уровень коэффициента R2 при оценке Зависимость регрессии: 1) только A \ 2) A и X; 3) от A, Chi S. S 0,301 A 0,189 S, X 0,688, X 0,21 3 S, X, A 0,695 A, X, S 0,695
Кажущаяся объяснительная сила переменной A Да, это было включено в качестве дополнительной переменной в уравнение Лед оказался меньше, чем когда он был впервые добавлен, Соответствующая объяснительная способность переменной S Включено в последнее уравнение. 6.8.
Предположим, что количество у определяется количеством В уравнении (6.1) Cov (x {, x2) равно нулю. Используйте это, чтобы упростить Формула для расчета коэффициентов множественной регрессии (5.12) В {И покажите, что это приводит к уравнению парной регрессии. как Почему вы выбрали спецификацию уравнения регрессии?
Смотрите также:
| Качество оценивания: коэффициент R2 | Влияние включения в модель переменной, которая не должна быть включена |
| Моделирование | Замещающие переменные |
Если вам потребуется заказать решение эконометрики вы всегда можете написать мне в whatsapp.

