Оглавление:



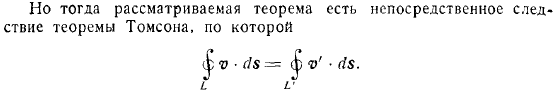

Теоремы Гельмгольца
Теперь докажите основные теоремы Гельмгольца. Теорема сохранения гидромеханики. Если мы сделаем те же предположения, что и теорема Лагранжа , то частицы жидкости, образующие вихревые линии, в какой-то момент образуют вихревые линии в течение всего. To докажем это, сначала рассмотрим вихревую поверхность, то есть ту, где вихрь скорости в каждой точке соприкасается с этой поверхностью. Такую поверхность можно получить, выделив несколько линий (они должны отличаться от вихрей) и пройдя через каждую точку этой линии вихря.
В один момент докажем, что частицы жидкости, составляющие вихревую поверхность, образуют вихревую поверхность в течение всего движения. Правда, на поверхности принимает бесконечный контур формула, скорость циркуляции по этому контуру равна. В следующий момент времени жидкостный контур принимает положение, и конечно, конечно. Находится на поверхности, образованной жидкими частицами, которые ранее составляли поверхность.
Теорема Томсона, скорость циркуляции по кривой во «времени» равна скорости циркуляции по кривой во времени, то есть равна нулю. Но из Формулы в этой контурной линии. Взять сколь угодно малую и можно расположить в любом месте на поверхности, но не обязательно в любой точке на поверхности. И это также означает, что поверхность является вихревой поверхностью. Теперь возьмите вихревую линию в данный момент. Пересекающиеся вихревые поверхности могут быть нарисованы через него.
Любое векторное поле, однозначное, непрерывное и ограниченное во всем пространстве, может быть разложено на сумму потенциального и соленоидального векторных полей. Людмила Фирмаль
В другие моменты частицы, составляющие поверхность сохраняемости векторных линий , образуют соответственно поверхности, в то время как частицы, составляющие пересечения поверхности, образуют пересечения поверхности, в каждой точке кривой. Вихри скорости должны находиться в плоскости как поверхности, так и поверхности. То есть эти касательные плоскости должны быть ориентированы вдоль точки пересечения, крест представляет собой касательную к линии.
Таким образом, линия является вихревой линией, теорема которой доказана. Таким образом, в рассматриваемом случае каждая вихревая линия сохраняет свою индивидуальность в том смысле, что каждая вихревая линия движется в пространстве вместе с составляющими ее частицами жидкости. Это свойство называется характеристикой сохранения вихревых линий, и название доказанной теоремы становится вполне понятным.
Следствие: при одном и том же предположении все вихревые трубки ограничены вихревой проволокой, которая всегда остается вихревой проволокой, поэтому они остаются в вихревых трубках во время движения. Точнее, этот результат следует понимать таким образом, что в какой-то момент частицы жидкости, образующие вихревую трубку, образуют вихревую трубку в следующий (или предыдущий) момент.
Теорема сохранения вихревой трубы. Если мы сделаем те же предположения, что и теорема Лагранжа, то сила вихревой трубы останется постоянной на всем протяжении. Дело в том, что прочность вихревой трубы в момент времени определяется циркуляцией скорости по контуру, охватывающему рассматриваемую вихревую трубу раз. Однако рассматриваемая теорема является прямым результатом теоремы Томсона.
Скалярная функция называется скалярным потенциалом, векторная функция называется векторным потенциалом. Людмила Фирмаль

