Оглавление:




Нелинейная регрессия
- Нелинейная регрессия После того, как переменная у связана с переменной х, Ударное отношение: y = a + No. + u, (4.28) Предположим, вы хотите получить оценку a, p и y со значениями y и x. Уравнение (4.28) Таким образом, в этом случае вы можете преобразовать его в линейное уравнение Нельзя применять нормальные процедуры оценки регрессии.
- Тем не менее, вы все равно можете получить оценки параметров Примените принцип минимизации суммы квадратов отклонений. Дальнейшее изучение Рим, проще говоря, это не потому, что вы должны использовать это сами Это понятно (исследователи обычно консультируются с экспертами Эконометрика), но это позволяет лучше понять идею Базовый регрессионный анализ.
Процедура лучше всего описана как последовательность шагов. Людмила Фирмаль
1. Возможные начальные значения параметров принимаются. 2. Прогнозируемое значение y рассчитывается исходя из фактического значения x s Используйте эти значения параметров. 3. Поскольку остатки рассчитываются для всех наблюдений в выборке, S — сумма квадратов невязок. 4. Незначительные изменения вносятся в одну или несколько оценок параметров.
5. Рассчитываются новые прогнозируемые значения для y, остатка и S. 6. Если S меньше, чем раньше, новая оценка параметра Вы должны использовать их в качестве новых отправных точек. 7. Шаги 4, 5 и 6 повторяются до тех пор, пока это не станет невозможным. Если вы измените оценки параметров, как это, Уменьшить S 8. Сделан вывод, что величина * Y минимизирована и получена окончательная оценка.
Параметр является оценкой наименьших квадратов. случай Давайте вернемся к примеру с бананом, описанному в разделе 4.1. Где у и х Связаны следующие зависимости: у = а + т + у. (4,29) Для простоты предположим, что os = 12 известно. Исследователи Однако необходимо определить только один неизвестный параметр. временно.
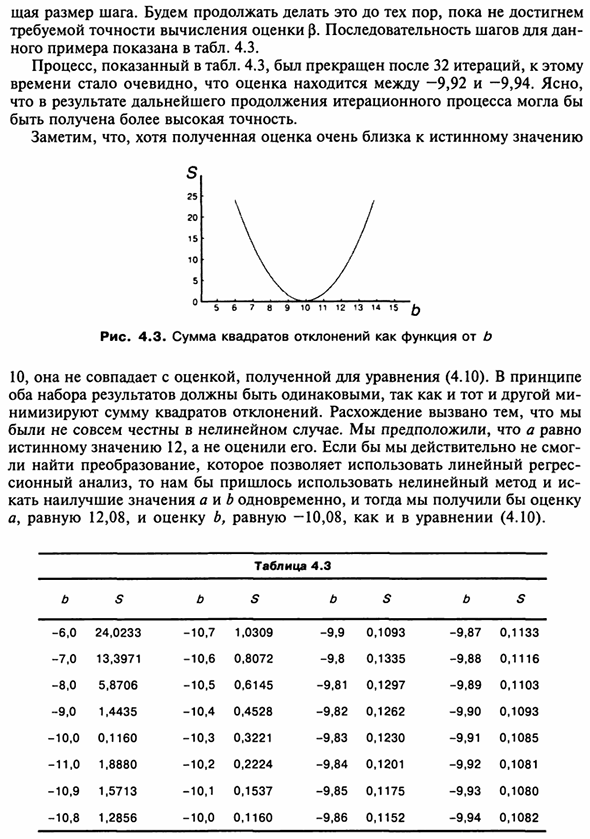
Я заметил, что есть форма зависимости (4.29), но я не могу догадаться об этом Вам необходимо применить преобразования, описанные в разделе 4.1. вместо Применить нелинейную регрессию. На рисунке 4.3 показано значение 5, которое можно получить в любое время Возможен выбор b для значений y и x, приведенных в таблице. 4.1. временно Давайте начнем с установки b в –6.0.
Уравнение принимает вид: * = 1 2- | (4,30) Рассчитать прогнозируемое значение у и остатка, основываясь на последнем Вычисляет значение 5 = 24,02. Затем подставьте b = -1. Значение S 13.40, то есть снизился. Таким образом, мы движемся в правильном направлении. Замена b = -8; 5 = 5,87. Давайте продолжим дальше. Если b = —9, значение равно 1,44; если b = –10, значение S составляет 0,12.
Когда b = -11, это 1,89. Очевидно, что при выборе b = –11 значение S определялось снова, поэтому оно перезаписывалось. Начал расти. Например, 0,1, получить значение — 10,9; -10,8 и т. Д. Начинайте двигаться дальше, пока не перестанет В меньших шагах (например, равных 0,01). Каждый раз включается Соблюдайте «бюст», измените направление в противоположную сторону и уменьшите Общий размер шага.
- Продолжайте делать это, пока не достигнете Точность p требуется для расчета оценки. Указанная последовательность шагов Пример этого показан в таблице. 4,3. Процесс показан в таблице. 4.3, закончено после 32 итераций Стало ясно, что расчетное значение составляло от -9,92 до -9,94. Очевидно В результате продолжения итерационного процесса дальше, Более высокая точность должна быть получена.
Обратите внимание, что полученная оценка очень близка к истинному значению S 25 20 15 10 5 6 7 8 9 10 11 12 13 14 15 fo Рисунок 4.3. сумма квадратов отклонений как функция от b 10. Не соответствует оценочное значение, полученное в уравнении (4.10). Как правило Оба набора результатов должны быть одинаковыми. Они минимизируют сумму квадратов отклонений.
Разногласия, мы Нелинейный случай не был полностью честным. Людмила Фирмаль
Истинное значение 12, не оценено. Если вы действительно не можете Найти преобразования, которые позволяют использовать линейную регрессию Анализ, то вы должны использовать нелинейные методы Напишите лучшее значение b одновременно и получите оценку Оценка равна 12,08, а b равно -10,08, как в уравнении (4.10).
Таблица 4.3 б -6,0 -7,0 -8,0 -9,0 -10,0 -11,0 -10,9 -10,8 5 24,0233 13,3971 5,8706 1,4435 0,1160 1,8880 1,5713 1,2856 б -10,7 -10,6 -10,5 -10,4 -10,3 -10,2 -10,1 -10,0 S 1,0309 0,8072 0,6145 0,4528 0,3221 0,2224 0,1537 0,1160 б -9,9 -9,8 -9,81 -9,82 -9,83 -9,84 -9,85 -9,86 S 0,1093 0,1335 0,1297 0,1262 0,1230 0,1201 0,1175 0,1152 б -9,87 -9,88 -9,89 -9,90 -9,91 -9,92 -9,93 -9,94 S 0,1133 0,1116 0,1103 0,1093 0,1085 0,1081 0,1080 0,1082 128 Основным недостатком нелинейной регрессии является оценка.
Намного медленнее чем линейный Россия, особенно Если чай нужно оценить некоторые параметры. Разработанная итерация Математически важные шаги Гораздо сложнее, чем описано в этом Однако до недавнего времени, даже при использовании этих шагов, Высокая стоимость компьютерных расчетов послужила тормозом приложения Нелинейная регрессия.
В последние несколько лет ситуация была: Для беспрецедентного увеличения мощности и скорости компьютера. В результате интерес к нелинейным методам начал расти, Удобное программное обеспечение, разработанное для обычных пользователей Чтение.
Смотрите также:
| Логарифмические преобразования | Выбор функции: тесты Бокса—Кокса |
| Случайный член | Иллюстрация: модель с двумя независимыми переменными |

