Расчет балок при изгибе на прочность

Расчет балок при изгибе на прочность

• В зависимости от поставленной цели расчета на долговечность, расчет балки в момент изгиба на долговечность может быть представлен тремя видами решаемых задач. 1. Проверьте напряжение балок при известных размерах поперечного сечения и заданных прочностных характеристиках материала. 2. Выбор поперечного сечения, то есть определение требуемых размеров поперечного сечения при заданной форме и прочностных

характеристиках материала (расчетные расчеты). 3. Конечная нагрузка определяется выбранными размерами поперечного сечения и прочностными характеристиками материала. Балка рассчитана с максимальными нормальными, тангенциальными и эквивалентными напряжениями. В данном разделе приведен расчет балок определенного сечения из пластического материала. Расчет прочности по максимальному нормальному напряжению.

Поскольку балки из пластического материала, как правило, выполнены из Людмила Фирмаль

симметричных сечений, то растягивающие и сжимающие напряжения крайних волокон одинаковы. Опасная часть балки становится участком, где возникает максимальный изгибающий момент Afxm ax, а опасная точка этого участка находится на расстоянии/ / max от нейтральной оси, где условие прочности в опасном участке записывается без учета знака изгибающего момента следующим образом: zmax=l^xmaxl Utak / ^x Ku»(21.14) 240gde#so-максимальное расстояние от нейтральной ОСИ до крайнего волокна поперечного сечения.Jx-осевой момент инерции поперечного сечения относительно нейтральной оси. Для симметричного поперечного сечения t/max=L / 2 условия прочности следующие: zmax=l^xm axl / ^x

Ry, (21.15) где Wx=Jx/h / 2 называется осевым резистивным моментом поперечного сечения. Спецификация момента сопротивления-м3 или см3. Таким образом, момент сопротивления является геометрической характеристикой прочности поперечного сечения балки при изгибе. Чем больше момент сопротивления, тем меньше стресс, который возникает в этой точке опасности. Момент сопротивления высоте h и ширине b прямоугольного сечения Wx = Jx/!/ Max=(bh9 / 12)/(n / 2)=BSC. Момент сопротивления W x радиусу G круглого сечения =Jx / r■ — w* / 4r=LGs. Сопротивление W * раз для наружного радиуса G кольцевого сечения Вт к икс =Jkx/r=n(r4-4r rty. Для профиля качения двутавровой балки канальный момент сопротивления показан в справочниках.

• Для выбора поперечного сечения балки (расчетный расчет) значение требуемого момента сопротивления определяется по следующей формуле: G xt R>(21.16)Cu Выберите размер этого сечения до полученного значения W x в заданном виде поперечного сечения. Определение предельной нагрузки осуществляется по формуле прочности (21.15). По известным значениям W x и r y вычисляется максимальный изгибающий момент абсолютной величины, который может выдержать данная балка: / Mx m axl=Wx Ry. (21.17) Затем, в соответствии с полученным значением|M x max|, определяется предельное значение внешней нагрузки, действующей на балку. 16-

480 241 расчет прочности при максимальном касательном напряжении. После расчета балки на нормальное напряжение выполняется проверка на прочность максимального тангенциального напряжения. Балка с определенной шириной поперечного сечения по высоте (прямоугольник, квадрат и др.).), Обычно не рассчитывают на тангенциальное напряжение, определяя его прочность нормальным напряжением. Исключение составляет балка с большой поперечной силой, или балка с резким изменением ширины сечения (двутавровая балка, швеллер и др.).да что с тобой такое? Опасным является поперечное сечение балки, а максимальная поперечная сила действует на Qmax. *

Otah=Otah^OTS/^x^St^s»(21.18) s otc-статический момент блокировки части поперечного сечения относительно нейтральной оси;Jx—момент инерции всего Людмила Фирмаль

поперечного сечения относительно нейтральной оси; DST определяется напряжением сдвига; — момент инерции всего поперечного сечения относительно нейтральной оси. Расчет силы эквивалентного напряжения. Расчет эквивалентного напряжения в основном основан на двутавровых балках, каналах,etc.At поскольку любая внешняя нагрузка, максимальный изгибающий момент и максимальная поперечная сила, возникающие сечения, обычно не совпадают, опасным сечением, большим изгибающим моментом и точкой бокового опасного сечения будет точка, в которой эквивалентное напряжение достигает наибольшего значения. Максимальное эквивалентное напряжение поперечного сечения балки создается в точках сопряжения горизонтальной и

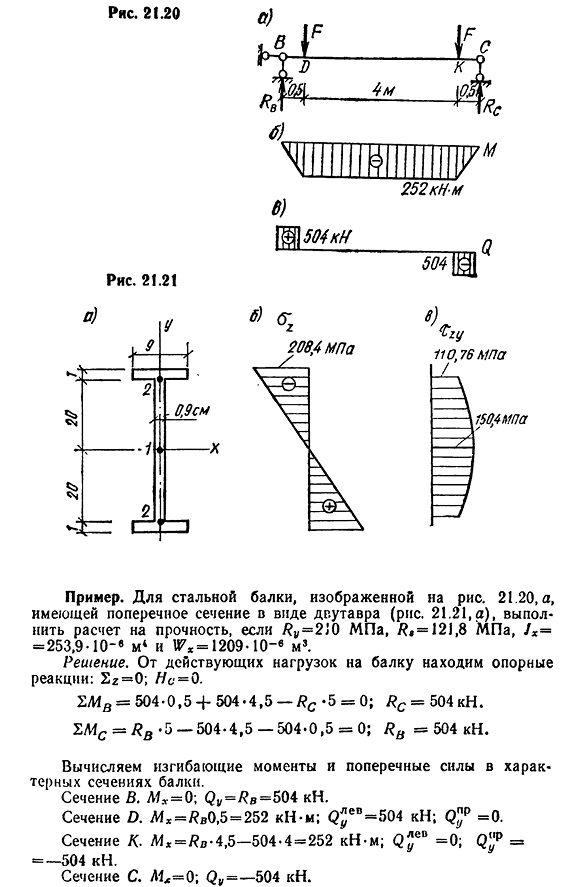
вертикальной стенок. Эквивалентное напряжение при расчете стальных балок рассчитывается по энергетической теории прочности. Условие прочности описывается следующим образом %kvtah=<1 ‘ 1E*Y(21.19), где Qz-Mxyljx—нормальное напряжение в критической точке;Vpy=qys0tcijxb-касательное напряжение в критической точке;RtJ-расчетное сопротивление стали. Рассмотрим процесс расчета более подробно на примере. 242 гонки 21.20 Например. Может быть. 21.20, а, имеет поперечное сечение в виде двутавровой балки(рис. 21.21,а), ры=2jQ МПа делать расчет на прочность, Ра=121.8 МПа, JX используется — =253.9-ИО-6M4 и АТИ=1209-ИО-6м3. Решение. Из приложенной нагрузки на балку находим опорную реакцию: S z=0;/ / C=0. =504-0, 5+504-4, 5-Rc-5=0; Rc=504kN. ZMc=RB-b— 504-4,5 — 504-0,5 = 0; RB=504kN. Рассчитайте изгибающий момент и боковую силу характерной части балки. Поперечное

сечение V. MX=0\Qy=Rg=504kN. В разделе D. MX=I 0, 5=252kN-m; Q * eB=504kN; Q » p=0. Раздел К. М,=р, б- 4,5-504-4=252kN-м;м джеб=0;м’*== — 504kN. Секция C. L1x=0; Qy= — 504kN. 1г* 243 согласно этим значениям, графики M и Q(фиг. 21.20, b и C). Расчет самого высокого нормального напряжения. В этой балке опасным участком, на который будет действовать максимальный изгибающий момент мшаха, будут все поперечные сечения сечения ДК. L1t Oh=252kN-м. Рассчитайте наибольшее нормальное напряжение в верхнем и Нижнем волокнах (рис. 21.21, 6). o2gaah = MT h / G h=252-103 / 1209-10 — «=208,4 МПа. Требования к прочности удовлетворяются, так как zmaxR s или

150,4>121,8. Расчет максимального эквивалентного напряжения. В этой балке опасные участки, в которых одновременно действуют максимальный изгибающий момент и максимальная поперечная сила, разделены на участки D и K. Afx=252kN-m и Qy=504kN. Опасной точкой этих секций является точка 2, т. е. место сопряжения вертикальной стенки с полками. Вычислим нормальное напряжение в этих точках:^, 2=L4x!/ 2 / ^x=252-103-2 0.1 0 -2 /2 5 3 ,9 -1 0 -» = 19,85 МПа. Предварительно рассчитанное тангенциальное напряжение в точке 2: Два. = Вычислить эквивалентное напряжение 110,76 МПа: около максимального env= 198,5® + 3-110,76″ = 283,2 МПа. Тэ Макс>1,15/?y или 283.2>241.5. 244балка не соответствует прочностным условиям максимальных тангенциальных и эквивалентных напряжений. Необходимо увеличить размер поперечного сечения.

Смотрите также:

Решение задач по технической механике

Главные нормальные напряжения и максимальные касательные напряжения при изгибе балки	Нормальные напряжения при косом изгибе
Понятие о теориях прочности	Касательные напряжения при изгибе балки