Оглавление:






Нормальные напряжения при изгибе балки
- Нормальное напряжение при изгибе балки — это изгибающий момент и боковая сила при изгибе балки в ее поперечном сечении. Рассмотрим случай простого изгиба (чистого изгиба), когда в поперечном сечении возникает только изгибающий момент. 21.10 а). Предположим, что поперечное сечение балки имеет ось симметричного ОУ, то есть главную центральную ось инерции, лежащую в плоскости изгиба, и другую главную ось, перпендикулярную ей. В зоне чистого изгиба балок выделяют два участка, отстоящих на расстоянии от опорных B до Z и Z+dz, и бесконечно измеряют длину малых элементов dz (рис. 21.10 б).
Действие левой части отброшенной левой части балки на этот элемент представлено в виде изгибающего момента MX. Действие правой отбрасываемой части балки на правую часть элемента dz представлено в виде основной силы czdA, которая приложена к каждой базовой платформе dA поперечного сечения и направлена параллельно оси Oz. Из шести уравнений равновесия элемент ygtri превращается в тождество, а именно: SX=0, 2U=0, 2M2= = 0, поскольку фундаментальная сила параллельна оси унции. Запишите три других уравнения равновесия элемента dz\ См х=с ЯЗДА=МХ;му=ХМУ=J х<JzdA=0(му)=0,а Поскольку плоскость
XOZ не имеет изгиба балки, W2=S Z = = \c tdA=0(поскольку внешний момент не дает проекции A, Людмила Фирмаль
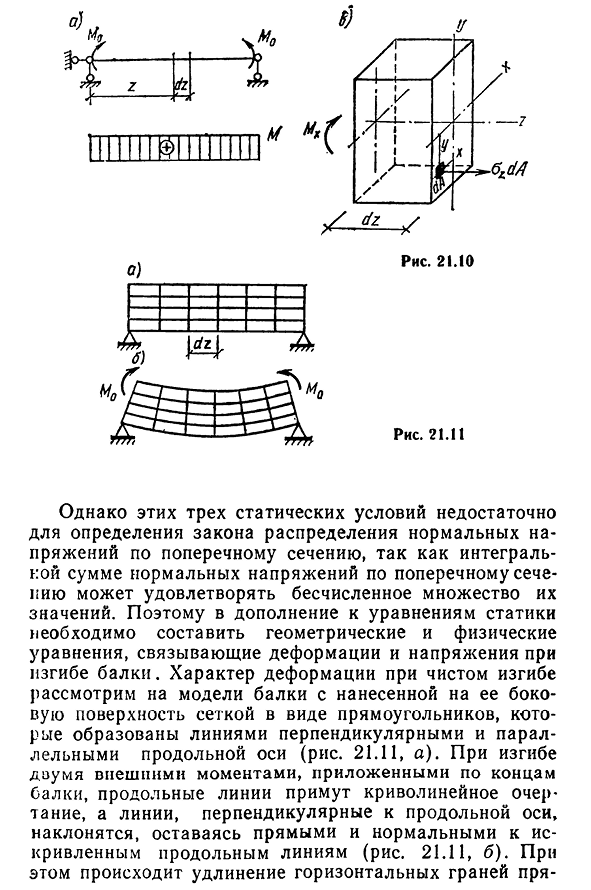
Nz=Q Сила осевой унции). 221, однако эти три статических условия, интегральная сумма вертикальных напряжений на поперечном сечении могут удовлетворять бесконечному числу его значений, поэтому закон распределения вертикальных напряжений на поперечном сечении, помимо уравнений статики, необходимо составить и физические уравнения деформации, связанные с напряжением при изгибе балки. Особенности деформации при чистом изгибе будем рассматривать в виде прямоугольника, который образован линией, параллельной вертикальной оси, с моделью балки, на которой сетка размещена сбоку( 21.11, а). При изгибе двумя внешними моментами, приложенными к концам балки,
вертикальная линия принимает криволинейный контур,а вертикальная линия наклоняется к вертикальной оси, изогнутой 21.11, б). В то же время, существует прямая горизонтальная плоскость удлинения- 222могоны на выпуклой стороне балки и укороченные на вогнутой стороне. Переход высоты пучка происходит постепенно от волокон, которые удлиняются, к волокнам, которые укорачиваются, поэтому между ними есть слой волокон, они изгибаются,но их длина изменяется такой слой Называется нейтральным слоем, а его след на плоскости поперечного сечения называется нейтральной линией или нейтральной осью. Предположим, что распределение наблюдаемой
- продольной деформации по сторонам балки внутри нее одинаково. Каждая линия сетки, перпендикулярная оси луча, является следом боковой плоскости стороны луча. Поскольку эти линии остаются прямыми, гипотеза плоского поперечного сечения справедлива для каждого поперечного сечения. Таким образом, поперечное сечение является плоским и перпендикулярным оси балки до изгиба, а также плоским и перпендикулярным изогнутой оси балки после изгиба, то есть поперечные сечения наклонены друг к другу. Для изучения деформации вновь рассмотрим мельчайшие элементы длины dzt, изолированные от балки (рис. 21.11, а). Таким образом, после изгиба
все продольно ориентированные волокна элемента изгибаются вдоль цилиндрической поверхности вблизи общего центра изогнутого С. крайняя часть поворачивается и образует между ними небольшой угол DTP(рис. 21J2, а). Обозначим радиус кривизны нейтральных волокон поперек реки. А волокна, отстающие от нейтрального слоя на расстоянии y, имеют радиус кривизны, равный p+ / L, поскольку кривизна продольных волокон для бесконечно малых элементов dz пренебрежимо мала (21.12, b). Показано абсолютное удлинение волокна TP, оно было разнесено на расстояние y от нейтрального слоя Adz. 223). 21.12
Значение Адз определяется из подобия треугольников CO{O2 и O2mmi}Dz Где kdz-ydzlp. Людмила Фирмаль
Относительное удлинение волокон TP z=kdzldz — = * y/p-при изгибе вводится предположение, что отдельные волокна балки не прижимаются друг к другу, и каждое из них подвергается простым условиям растяжения или сжатия. Используя зависимость крюка при растяжении O = E, получен закон распределения нормального напряжения по сечению при изгибе. (21.3) таким образом, в поперечном сечении балки в каждой точке нормальное напряжение пропорционально расстоянию этой точки от нейтральной оси и не зависит от координаты X. Поскольку полученная формула включает неизвестное значение радиуса кривизны P, то определить численное значение нормального напряжения oz оттуда невозможно.
Определить положение нейтральной оси поперечного сечения из условия, равного нулю вертикальной силы Nz. Для этого Уравнение 224b статики 2z=0 подставляет значение O2, и мы получаем 2z паза=F сбыл.да=Ф(ЕС/Р)DА=(Е/Р)Ф ыда=0. А. А. От£ / p=#0, то J ydA=0, и представляет Статический момент поперечного сечения. Он равен нулю только в том случае, если ось ox проходит через центроид сечения. В результате нейтральная ось в сетчатом изгибе балки проходит через центр тяжести поперечного сечения, от которого расстояние y необходимо отсчитать при определении нормального напряжения (T2). Назначим уравнение статики 244^=0 для уравнения VG=EU/p, получим S m y=[xoz dA=(E/R) [xydA, Один Фунт / p=y=O,
то[xyda=0 и так далее Центробежный момент инерции секции. Она равна нулю только по отношению к главной центральной оси инерции. В нашем случае ось OU является осью симметрии, поэтому ось OU и ось ox являются главной центральной осью инерции секции. Теперь найдем зависимость между кривизной 1/р в поперечном сечении балки и изгибающим моментом. В уравнении статического равновесия 244X=0 получается путем подстановки уравнения [VG=EU] p M x=f (E^/R) dA=(E/R) [y H A. Один Где Jx=J y2dA представляет собой главный CEI-A Момент инерции оси тролля к центральной оси секции. Затем Mjc=EVx / p или 1/.p=M X!E J X (21.4) Продукты EJX
вызваны жесткостью на изгиб луча, которая характеризует способность сопротивляться погнутости. Присвоив формуле (21.4)значение 1, Ip=azylEt получим величину перпендикулярного изгибающего напряжения балки, выраженную в терминах изгибающего момента, геометрической характеристики поперечного сечения- 15-480 225 поперечного сечения JX и расстояния от точки задачи до нейтральной оси поперечного сечения y Oh: < 5g=M x Y и x. (21.5) Наибольшее вертикальное напряжение изгиба y=y^^в самом дальнем волокне поперечного сечения от нейтральной оси. : a^=x Y t x^x — График нормального напряжения в поперечном сечении показан на рисунке. 21.12 г.
Смотрите также:
Решение задач по технической механике
Если вам потребуется заказать решение по технической механике вы всегда можете написать мне в whatsapp.

