Оглавление:





Базисная процедура
- Основная процедура Одним из недостатков линейного регрессионного анализа является то, как он должен быть Из самого названия это означает, что оно может применяться только линейно Уравнение. Для простого регрессионного анализа речь идет об уравнениях Типы явлений y = a + $ xxi (4.1).
- Состоит из независимых постоянных значений (может не существовать). Моделируемая переменная, умноженная на коэффициент и случайную величину Нарушение остаточного срока, которое можно временно игнорировать. о В этом случае линейное уравнение За исключением постоянных значений, мент записывается как произведение ne. Пояс и модуль: >; = cx + p1x1 + p2; c2 + … (4.2) Форма уравнения * = «+ F (4.3) и y = ois * (4.4) Это нелинейное.
Выберите и нанесите а и (5 значений, Вы можете видеть, что оба представлены кривыми. Людмила Фирмаль
Зависимости (4.3) и (4.4) считаются приемлемыми для описания кривой Энгель характеризует связь между конкретными требованиями 115 var (y) и общий доход (x). Как я могу определить параметры А и Р Каждое уравнение, которое знает значения у и х? Наконец, в любом случае может быть применена линейная регрессия. Анализ, это требует небольшой подготовки.
Во-первых, чтобы Обратите внимание, что уравнения (4.1) и (4.2) являются линейными в двух направлениях. Это верно Если вы определяете переменную в показанной форме, часть является линейной в переменной, Как функция. Следовательно, он состоит из взвешенной суммы переменных, Параметр вес. Например, в уравнении (4.1) просто xv a Это не бревно (х {).
Правая сторона также линейна по параметрам. Взвешенная сумма параметров, а переменная x в этом случае Ваш собственный. Только для целей линейного регрессионного анализа Ко второму типу линейности. Переменная нелинейность всегда можно обойти Используйте соответствующее определение. Например, Формат соотношения следующий: y = a + M1 2 + p2l /^»+..- <4-5) Если вы определите z {= x {2, z2 = n / * 7 и т. Д.
Дисплей: y = a + ^ zx + $ 2z2 + ^ (4.6) И теперь она линейна как по переменным, так и по параметрам. Этот тип трансформации является поверхностным и обычно Уравнение регрессии записывается в виде нелинейного уравнения для Пояс. Это позволяет избежать ненужных обозначений. С другой стороны, уравнения типа (4.4) нелинейны как пара Метры и переменные не могут быть преобразованы просто заменой Определение.
Не думаю, что вы можете преобразовать его в линейный, Если мы определим z = xP и заменим jfl вместо z \, потому что p неизвестно, Вы можете рассчитать примерное значение z. ) Соотношение линейных параметров обсуждается в следующем разделе. Тем не менее, все, что вам нужно сделать в случае (4.3), это решить Залейте z = (1D). Уравнение (4.3) принимает вид: >> = «+ Pr, (4.7) И это становится линейным. В этом случае оцените регресс без проблем Это между у и г.
Постоянный член уравнения регрессии Является оценочным значением а, а коэффициент z является оценочным значением (J. случай Предположим, вы изучаете связь с годовым потреблением БА. Нан и годовой доход и результаты наблюдений приведены в таблице. 4.1 Место сбора 10 семейных наблюдений (пока забудем о z) — Рисунок 4.1. Представлено облако точек, соответствующее наблюдению, И график уравнения регрессии между y и x: 116 £ = 5,09 + 0,73 *; L2 = 0,64. (4.8) (Co.) (1,23) (0,20)
Рисунки с 4.1 по 4.1 показывают, что график уравнения регрессии не полностью совместим Коэффициент х по существу Отличается от нуля на уровне значимости 1%. Очевидно, что Точка наблюдения находится на кривой, а уравнение регрессии Генерируется напрямую. В этом случае легко увидеть, что это функционально Соотношение между у и х определено неправильно.
- Если ты не можешь Зависимости могут быть представлены в графическом формате (например, Знает, что где-то разрешено). Можно использовать ошибку, анализ остатков. В этом случае значение Таты перечислены в таблице. 4.2. Таблица 4.1 Emia 1 2 3 4 5 6 7 8 9 1 0 банановый (Фунт) (Y), 1,93 7.1 3 8,78 9,69 10,09 10,42 10,62 10,71 10,79 11,1 3 доходов (10 000 долларов) (Х) 1 2 3 4 5 6 7 8 9 1 0 (Z) 1000 0500 0,333 0,250 0, 200 0,167 0,143 0,125 0,11 1 0100
Положительные или отрицательные, большие или маленькие остатки Случайно чередуется. Здесь, как вы можете видеть из таблицы, Тат отрицательный, затем становится положительным и достигает мака минимум, и снова уменьшается и становится отрицательным: это раньше Это считается очень подозрительным.
В этом примере значения >> и x были получены с использованием метода Монте Карло, истинное соотношение: Людмила Фирмаль
Y = 12 + случайный член, (4.9) x принимает целочисленное значение от 1 до 10, а значение случайного члена равно Используйте случайные числа с нормальным распределением в среднем 0 и стандартное отклонение 0,1. Если вы знаете это и определите z = 1 / x, уравнение будет линейным Форма (4.7). Значения Z для каждого семейства уже рассчитаны в таблице. 4.1.
Ценить В регрессии между y и z: 9 = 12,08-10,08; L2 = 0,9989. (Ко) (0,04) (0,12) Подстановка z = 1 / x дает £ = 12.08-10.08 (4.10) (4.11) Таблица 4.2 семья 1 2 3 4 5 6 7 8 9 1 0 1,93 7.1 3 8,78 9,69 10,09 10,42 10,62 10,71 10,79 11,1 3 5,82 6,56 7,29 8,03 8,76 9,50 10,23 10,97 11,70 12,43 -3,90 0,57 1,49 1,67 1,33 0,93 0,39 -0,26 -0,91 -1,31 11 8 Учитывая высокое качество формулы оценки (4.10), это не удивительно Соотношение (4.11) близко к истинному уравнению (4.9).
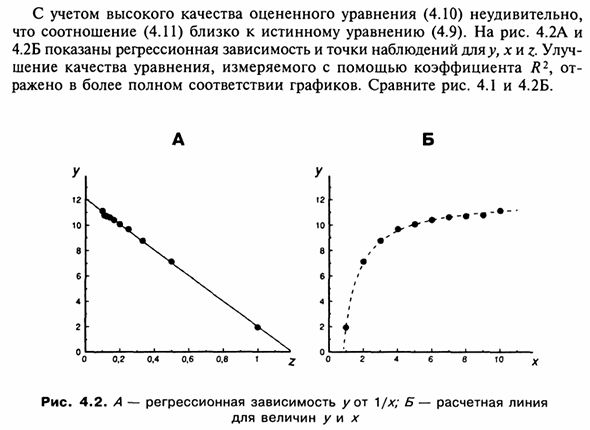
Рисунок 4.2А и 4.2B показывает >>, x, r Улучш регрессионная зависимость и точки наблюдения Качество уравнения измеряется с использованием коэффициента R2 Отображается в полном соответствии с графиком. Сравните фотографии. 4.1 и 4.2В. * — * Рисунок 4.2. Зависимость регрессии Y от A-L / x; линия расчетов B Количество у \ л х
Смотрите также:
| F-тест на качество оценивания | Логарифмические преобразования |
| Взаимосвязи между критериями в парном регрессионном анализе | Случайный член |

