Проверка гипотез, относящихся к коэффициентам регрессии

Проверка гипотез, относящихся к коэффициентам регрессии

• Коэффициент гипотезы регрессия Как начать статистическое исследование — с теоретического состава Расстановка переносов или эмпирический анализ? На самом деле, теория и практика Тики будут богаты друг с другом, и никакие подобные вопросы не будут заданы. так Рассмотрим проблему проверки гипотезы с двух точек зрения. использовать.

• С другой стороны, вы можете предположить, что гипотеза сформулирована первой. Цель эксперимента — определить его применимость. Приведет Проверьте гипотезу о значимости. Тем временем первый профессионал После экспериментов определите, какая теоретическая гипотеза Следите за результатами эксперимента. Это приводит к строительству основного ный интервал.

Мы уже знаем логику, которая является основой для построения стандарта значения. Людмила Фирмаль

Описано в разделах Мосты и доверительные интервалы и Курсы по вводной статистике. Поэтому мы уже понимаем большинство понятий, используемых в регрессии. Сионский анализ. Однако один вопрос может быть новым. Используйте одностороннюю ссылку. Такие критерии применяются к рег Весенний анализ очень распространен. На самом деле они есть или должны быть Здесь традиционно чаще встречаются двусторонние стандарты, Преподается в учебниках.

Поэтому важно понимать их полезность, когда: Измени, дорога к этому представляет собой серию небольших Шаг роспуска. Ничего из этого не сложно, Чтобы сделать путь короче, хуже, Попытки сократить общую процедуру до нескольких механических применений Формула, вы столкнетесь с большими трудностями.

Формулировка гипотезы Начнем с предположения, что формулировка гипотезы предшествует Что означает связь между экспериментом и предположением? Отравление. Например, общий уровень инфляции Кандидаты (/ 5, процентов) зависят от роста инфляции. Заработная плата (в процентах) и это соотношение является линейным Уравнение: / 7 = куб. См + рН> + ш, (3,34) Где a и p — параметры, а u — случайный член.

Тогда вы можете предположить, Влияние случайных членов, исключая общую инфляцию Эквивалент инфляции из-за повышения заработной платы. В этих условиях вы можете Скажите, что гипотеза, которую вы пытаетесь проверить, считается нулевой, Он представлен H0 и состоит в том, что P = 1. Гипотеза, обозначенная I и представляющая собой заключение.

Это тот случай, когда экспериментальная проверка показывает мошенничество H0. в В этом случае эта гипотеза p * 1. Сформулированы две гипотезы Фургоны с использованием следующих обозначений: I 0: p = 1; #,: P * 1. В данном конкретном случае общая инфляция Равный инфляции, вызванной ростом заработной платы, мы пытаемся Защищаясь, применяя нулевую гипотезу H0 к самому строгому тесту, Я надеюсь, что она не будет спорить.

Однако на практике более общий Построение нулевой гипотезы затем проверяется с использованием Общая альтернативная гипотеза. Это похоже на правду. Например, Давайте посмотрим на простую функцию спроса: y = a + px + w, (3.35) Где у — величина спроса на продукты питания, а х — доход. В процессе Исходя из очень разумного обоснования, вы предполагаете, что спрос.

Еда зависит от дохода, но вашей гипотезы недостаточно на «, чтобы иметь возможность определить конкретное значение для р. Вы можете использовать для, чтобы установить зависимость величины у от х. Когда нулевая гипотеза принята, Утверждают, что величина y не зависит от x, то есть P = 0. Основной гипотезой является pΦ0, то есть значение xinf Если у может отклонить нулевую гипотезу, Далее, хотя бы в общих чертах, определим наличие зависимостей.

Используя введенную нотацию, ноль и альтернативу Каждая гипотеза принимает следующую форму: # 0: p = 0 и #,: p * 0. Следующее описание относится к модели парной регрессии (3.1). Это Относится только к коэффициенту наклона p, но точно такой же Процедура распространяется на постоянных членов.

Возьми общий случай Нулевая гипотеза состоит в том, что р является особенно специфичным м значение, например, р0, и альтернативная гипотеза состоит в том, что р Равен этому значению (H0: p = po; H {: P * P0). Вы можете попробовать Ку отклонить или подтвердить нулевую гипотезу в зависимости от того, что Требуется в этом случае. Предположим, четыре условия Гаусс — Марков доволен.

Вывод гипотетических результатов Если гипотеза H0 верна, оценка p получена во время регрессии Распределение с математическим ожиданием анализа, ро и дисперсии Это G2J [n Var (x)] [справочная формула (3.25)]. Здесь, О ОС Это точный термин и имеет нормальное распределение. В этом случае количество Как показано на рисунке B, B также нормально распределен.

3.4. сокращение Функция плотности вероятность б Pcr2sd po-sd po P „+ sd p> + 2sd b Рисунок 3.4. Структура нормального распределения оценивается в% Стандартное отклонение d от математического ожидания. «На рисунке это соответствует стандартному отклонению расчетного значения b. То есть J v u (у Расчетное значение параметра P находится в пределах двух стандартных отклонений P0 (если гипотеза I0 верна: p = po).

Сначала предположим, что вы знаете стандартное отклонение б ранг. Это правдоподобное предположение и будет отброшено позже Ему. На самом деле важность этого отклонения (и неизвестно Значения параметров А и Р) подлежат оценке. Тем не менее, это может быть упрощено Предполагая, что вы знаете точное значение отклонения, Часто есть возможность создать график (рисунок 3.4).

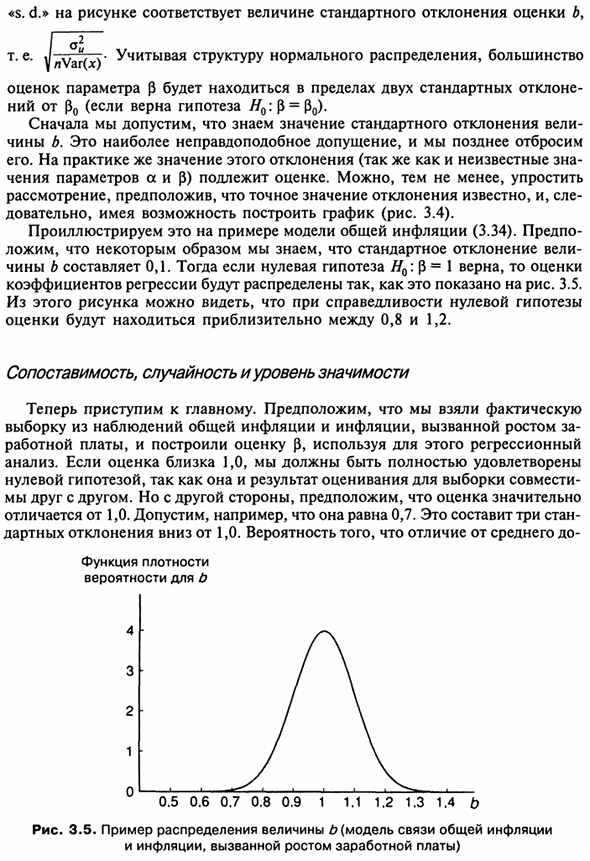
Это иллюстрируется на примере модели общей инфляции (3.34). до Предположим, вы знаете, что стандартное отклонение было получено каким-то образом б ранг 0,1. Нулевая гипотеза H0: оценивается, если p = 1 верно Коэффициент регрессии распределяется, как показано на рисунке 3.5. Из этого рисунка, если нулевая гипотеза верна, Расчетное значение составляет около 0,8-1,2.

Сопоставимость, случайность, уровень значимости Давайте объясним основные моменты. Предположим, вы на самом деле взяли Образец наблюдений за общей инфляцией и ростом инфляции Построить оценку р с использованием заработной платы и регрессии для этого Анализ. Если оценка близка к 1,0, вы должны быть полностью удовлетворены Нулевая гипотеза, результаты оценки выборки, совместимые с ней Мы друг друга.

Но с другой стороны, оценочная стоимость Отличается от 1.0. Например, предположим, 0,7. Будет три лагеря Отклонение дротика от 1,0. Отличие от среднего Функция плотности вероятность б 4 3 2 1 0,5 0,6 0,7 0,8 0,9 1 1,1 1,2 1,3 1,4 б Рисунок 3.5. Пример распределения стоимости б (модель взаимосвязи между общей инфляцией Инфляция из-за роста заработной платы) 92 3 стандартных отклонения могут быть положительными или отрицательными Сторона только 0,0027, то есть очень низкая.

На основании этого я называю В результате беспокойства можно сделать один из двух выводов. 1. Нулевая гипотеза P = 1.0 верна Эксперимент дал случайные результаты. Вероятность (3 очень маленький, но тем не менее Она случается в 0,27% случаев, и вы предполагаете, что это один Случай. 2. Можно сделать вывод, что гипотеза противоречит результату Оценка регрессии.

Не в восторге от описания Poon kte 7, вероятность настолько мала, что вы можете понять, что это наиболее разумно Хорошее объяснение состоит в том, что р не точно равен 1,0. Другими словами, принять альтернативную гипотезу I, P * P 0. Как вы решаете, когда выбрать первый выход? Когда второй? Очевидно, что чем ниже вероятность построения регрессии, Подобно тому, что мы получили в предположении, что гипотеза верна Выбор второго вывода, скорее всего, отвергнет гипотезу.

Как мало Должна ли быть определенная вероятность выбора второго заключения? На этот вопрос нет однозначного ответа. Самое большее Экономическая работа на важном уровне занимает 5 или 1%. Если выбран 5%, переключение на второй выход происходит, когда Вероятность получения таких экстремумов, если нулевая гипотеза верна Значение b составляет менее 5%.

• В этом случае они являются нулевой гипотезой Должен быть отклонен с уровнем значимости 5%. Это происходит, когда значение b находится дальше от P0 1,96 стандартное отклонение. Глядя на нормальный стол Глядя на раздачу (последняя вкладка AL книги) б превышает среднее значение более чем на 1,96 стандартов. Отклонение составляет 2,5% и, аналогично, Это значение имеет стандартное отклонение ниже среднего более 1,96 Значение также составит 2,5%.

Общая вероятность того, что это значение исходит от На основании ожиданий стандартного отклонения выше 1,96 Поэтому Ния составляет 5%. Чтобы обобщить это важное правило в математической форме: Когда нулевая гипотеза отвергается Z> 1,96 или Z <-1,96, (3,36) Где Z — регрессионная оценка и Значение потенции с. *

Разница в баллах регрессии И ^^ ~ По виртуальным ценностям стандартное отклонение (Z?) Людмила Фирмаль

Нулевая гипотеза не отвергается если -1,96 2,58 или Z <-2,58. (3,42) Возвращаясь к таблице нормального распределения, вы можете увидеть: Тот факт, что значение b превышает 2,58 стандартного отклонения Увеличение математического ожидания, такая же вероятность на 0,5% Вероятность состоит в том, что b ниже математического ожидания. Дания имеет стандартное отклонение более 2,58.

В целом Вероятность получения такого экстремального значения составляет 1%. в 94 По крайней мере, если коэффициент равен 3, нулевая гипотеза (3 = 1,0 Коэффициент регрессии больше 1,258 или меньше 0,742. Вы можете быть удивлены: почему исследователи обычно представляют Это результат уровня значимости 5 и 1%? Почему не достаточно Есть только один уровень?

Причина обычно в Попробуйте сбалансировать риск создания мисс I и IIroda. Ошибка Ирода возникает, когда вы отвергаете истинный ноль. Гипотезы. Если вы не откажетесь от поддельной гипо, вы получите ошибку IIrod Thesis. Я и II ошибки в повседневной жизни Проблема того, как избежать ошибок типов 1 и 2, известна всем. T Ярким примером этого является уголовное расследование Step.

Примите следующие параметры для нулевой гипотезы Дима невиновен и суд Случайно виноват. Ошибка типа 2 Когда судьи дзю ошибочно не виноваты Ответчик. Очевидно, что чем ниже критическая вероятность, тем ниже риск. Вы получите первый тип ошибки. Когда использовать уровень значимости Если 5%, отклонить истинную гипотезу в случае 5%.

Когда важен уровень ty равен 1%, а в случае 1% он совершает ошибку первого типа. Вот так В этом отношении уровень важности 1% является более надежным. если Если вы отвергаете гипотезу на этом уровне, вы почти наверняка Из-за этого, 1% уровень важности Называется «выше» по сравнению с уровнем 5%. В то же время, если нулевая гипотеза неверна, уровень значимости высок чем шире диапазон принятия гипотез.

Вы не откажетесь от этого, и вы подвержены повышенному риску ошибок второго рода. так Вы сталкиваетесь с дилеммой. Если вы так сильно придерживаетесь Высокий уровень значимости, вы столкнетесь с относительно высоким риском Если гипотеза неверна, вы совершаете второй тип ошибки.

Если вы выбираете Если менее важно, столкнуться с относительно высоким уровнем Риск совершения ошибки первого типа, если гипотеза верна. Большинство людей выбирают довольно простой формат, который обеспечивает га Царапина и проверка на обоих важных уровнях, Результат каждой такой проверки. На самом деле часто не нужно Ссылка на оба результата напрямую.

Значение b «Экстрим» гипотезы отклонен на уровне 1% Не важно, но не 5 процентов. Процентный уровень, теперь автоматически отклонять Уровень значимости составляет 5% и не нуждается в упоминании. если Но вы не откажетесь от гипотезы этого автомобиля с уровнем значимости 5% С точки зрения математики, не отвергая, на уровне 1%, Нет смысла говорить о ценности, и это снова.

Только в одном случае Оба результата должны быть представлены: если гипотеза отклонена на 5% Г-н .. Тем не менее, важность не 1 процент. Что произойдет, если стандартное отклонение b неизвестно? До сих пор мы предполагали, что стандартное отклонение величины b известно. Однако на практике это предположение нереально. Это можно проиллюстрировать на примере. Стандартная ошибка величины b, полученная из уравнения (3.27).

Свинец Два изменения в процедуре проверки гипотез. Во-первых, значение Zopre Разделить, используя стандартную ошибку co. (B) вместо Стандартное отклонение называется s.d. (b) и / или статистикой: -7 м * G (143) Во-вторых, критический уровень / Это называется распределением f вместо нормального распределения. не Объясните почему или объясните математически / распределение математически.

Достаточно сказать, что это связано с нормальным распределением. Точный формат зависит от количества степеней свободы регрессии и является Приближается к нормальному распределению по мере увеличения Степени свободы. Конечно, вы уже встречаете концепцию / -распределения Вводный курс по статистике. В таблице. А.2 в конце книги — критик Группировка по / значению, уровню значимости и количеству групп Хорошо.

Оценки для каждого параметра в уравнении регрессии поглощают одно Бесплатный пень образца. Следовательно, число степеней свободы равно числу Значение наблюдения выборки за вычетом количества оценочных параметров. параметры Они являются постоянными членами (если они введены в регрессионную модель) Эти) и независимые переменные коэффициенты.

Когда рассматривается В парной регрессии оцениваются только два параметра a и p, поэтому число Степень свободы n-2. Основываясь на множественном регрессионном анализе, вам понадобится более общий Ярость. Критическое значение / отображается как / да и заменяет число 1,96. В формуле (3.39). Следовательно, регрессионная оценка Если нулевая гипотеза p = p0 отклоняется: £ -P o ~ * Crit <с Q (A) <* crit- (3.44) случай В разделе 2.6 функция расходов на питание.

Личный располагаемый доход на основе годовых данных 96 В Соединенных Штатах в течение 25 лет (1959-1983) уравнение регрессии предварительно Установить по формуле (2.42): >> = 55,3+ 0,093 * (3,45) (2,4) (0,003) Число в скобках является стандартной ошибкой. Предположим, одной из задач оценки регрессии было подтверждение В ожидании предчувствия, что уровень стоимости еды зависит от размера Доход.

Поэтому мы формулируем нулевую гипотезу о том, что величина Поскольку p равно нулю, мы его опровергнем. относящиеся T-статистика, рассчитанная по уравнению (3.43), является оценкой коэффициента. Значение делится на стандартную ошибку: 6- П о-ф 0,093 _ ‘- ^ ^ — ^ ^ -оооз’ <3-4 6) Выборка содержит 25 наблюдений, и поскольку мы оценили два параметра, Количество степеней свободы составляет 23.

Критическая ценность 5 / Центральный уровень значимости 23 степени свободы составляет 2,069. далее / -статистика не находится между 2,069 и -2,069. Так цель Уравнение (3.44) не выполняется, поэтому отвергаем нулевую гипотезу, Поскольку р на самом деле отличается от нуля, следователь Однако сумма дохода влияет на уровень расходов на питание.

Если этот критерий написан словами, 2,5 процента от верхнего и нижнего пределов Хвост / распределение начинается со стандартного отклонения 2.069 И его математические нулевые ожидания упали. Коэффициент регрессии По оценкам, это в пределах 2,069 стандартных отклонений Из гипотетического значения мы не будем отказываться от последнего.

На рассмотрении В этом случае расхождение соответствует 31,0 стандартных отклонений, И результат оценки регрессии Поговорим о нулевой гипотезе. Конечно, используйте уровень значимости 5% в этом смысле. Новая функция проверки гипотез, предполагаемый риск составляет 5% Первый тип ошибки. В этом случае риск может быть снижен до 1%.

Уровень значимости 1%. Критическая ценность / Текущий уровень значимости 23 степени свободы составляет 2,807. Используйте Мы видим, что от этой цифры отношения (3.44) можно легко отказаться. Существует также гипотеза об этом уровне значимости. Процедура установления связи между зависимостью и описанием ne Сформулируйте нулевую гипотезу об отказе Его (3 = 0, очень часто используется.

Так что в большинстве случаев Не все регрессионные программы автоматически выводят / статистику для этого Особый случай, то есть коэффициент делится на его стандарт Полная ошибка Это соотношение часто называют «/ -с» Статистика информации. » Однако, если нулевая гипотеза определяет значение, отличное от нуля p, следует использовать более общую формулу (3.43). / -Статистика рассчитывается вручную.

Например, рассмотрим модель регрессии снова Между общей инфляцией и инфляцией из-за роста заработной платы (3.34) выбранное уравнение регрессии имеет вид Следующее (стандартная ошибка показана в скобках): р = -1,21 + 0,82 *. (3,47) (0,05) (0,10) В конечном счете, если мы проверим гипотезу общей инфляции N период равен инфляции из-за роста заработной платы.

Нулевая гипотеза состоит в том, что коэффициент w равен 1,0. Корреспонденция / статистика принимают следующую форму: £ -Ro _ 0,82-1,00 _ » ^ G odo- «1 D <3-48) Если образец содержит 20 наблюдений, следующие частоты Bo составляет 18 и 5% уровня критического значения Значение составляет 2101. В этом случае / -статистика находится между 2101 и 2101.

Напротив, нулевая гипотеза не отвергается. Оценка 0,82 ниже Виртуальное значение 1,00, но недостаточно низкое для исключения Рассмотрим возможность правильности нулевой гипотезы. Срок принятия (отклонения) гипотезы В этом разделе было показано, что нулевой ги должен быть отклонен. / -статистика больше чем t m или меньше чем ~ tKpum Если // статистика взаимосвязана, эту гипотезу не следует отвергать D ~~ 1крит также покрыт — почему «не отклоняйся», почему это сложно?

Не имею Для / -статистики проще сказать принять гипотезу ~ Между tKpum и tKpuml Мнения против использования термина «согласен» Уметь «принимать» несколько взаимоисключающих гипотез В то же время Так в примере с отношением к общему Инфляция из-за инфляции и повышения заработной платы, вы не Вы можете отклонить нулевую гипотезу № 0: P = 0,9 или нулевую гипотезу Zo H0: p = 0.8

Логично сказать, что вы не отвергаете эти нулевые гипос Как и в случае нулевой гипотезы Я0, эти документы: (J = 1,0, учитывая вышеизложенное, но Сказать, что вы в то же время почти бессмысленно Есть все три гипотезы. В следующем разделе вы увидите, что вы можете: Определите много гипотез, которые не могут быть отклонены В результате этого эксперимента.

Так что было бы небрежно выбирать Один из них «одобрен». ^ Объяснение результатов теста по критериям Предположим, что есть теоретические отношения у = а + (до: + и 98 И ноль, и альтернативные гипотезы даются в виде / 0: P = p o, И { : PΦP0. Для P, если оценка b получена из выборочных данных, 5% и одна область принятия и отклонения гипотезы Уровень значимости в процентах, как правило, может быть выражен 3.7 на левой стороне рисунка.

Правая сторона 3.7 рисунка показывает те же самые области Новый пример регрессионной модели между общей инфляцией и инфляцией Она была вызвана ростом заработной платы. Между тем, нулевая гипотеза Формат p = 0. Нулевая гипотеза не отклоняется на уровне Если значение b находится в пределах 2101-го числа, оно не является значимым при 5% Погрешность дротика от единицы, т.е. в диапазоне от 0,79 до 1,21, не так b отклонен с уровнем значимости 1

В пределах 2878 стандартных отклонений от единицы, то есть Диапазон составляет от 0,71 до 1,29. На рисунке 3.7 показано, что существует три типа приемных зон Решение. 1. Область, где значение b далеко от гипотезы Значение P отклонено как 5% от нулевой гипотезы и уровень значимости 1%. 2.

Область, где значение b достаточно далеко от гипотезы P-значение, так что нулевая гипотеза отклоняется на 5 Это цент, но это не 1% уровень важности. 3. Область, где значение b достаточно близко к гипотезе Значение р, так что нулевая гипотеза не отклоняется Один из двух рассмотренных уровней значимости. Исходя из схемы, нулевая гипотеза.

Если он отклоняется на уровне важности 1%, он будет автоматически Даже уровень 5% отклоняется. И поэтому Случай 1, нужно только заявить об отклонении одной гипотезы Уровень значимости. Объявить отказ с 5-про Центральный уровень не нужен. Это эквивалентно Сделайте заявление о возможности того, что парашютист имеет высоту 2 м, затем.

Кроме того, объявить способность принимать высоту 1, 1,5 метра Аналогично, только для случая 3 В этом конкретном случае гипотеза Отклонено на 5% уровне значимости. Автоматически отсюда То есть он не отклоняется на уровне 1 процента. Добавление к этому утверждению имеет тот же эффект, что и В заявлении, что прыгуны в высоту не могут принять высоту 1 1,5 м, добавил заявление, что он не может быть высоким.

В пределах 2 м Результаты должны быть представлены только в случае 2 (предпочтительно) Проверьте оба. Рисунок 3.7. ^ Отображение результатов проверки гипотез на основе критериев (Заключение в скобках не обязательно) Вывод на дисплей результатов оценки Развитие регрессии, в некоторых работах, в скобках Вместо стандартной ошибки предоставляются коэффициент / статистика.

Вы доллар Жена внимательно следит за этим и, представляя результаты, Это должно быть сделано очень четко. упражнения 3,7. Приведите еще несколько примеров для обычных людей. Ошибка может произойти при принятии решений первого и второго типа. 3,8. До начала курса было протестировано 36 студентов. Тест на способность.

Результаты тестовых и тренировочных курсов (по типу «pass» / «Отказ») отображается в таблице p. 101. Как вы думаете, тест способности поможет вам набирать? Если так, как вы определяете проходной балл? (Обзор Выберите компромисс между типом I и типом II ошибки, связанные с выбором Проходной бал Лама) 3,9. Стандартная ошибка коэффициента при t в упражнении 2.1 составила 0,08.

Истинное значение коэффициента проверяет нулевую гипотезу, такую ​​как Но ноль: 1) 5% уровень значимости. 2) Уровень важности составляет 1%. 3.10. В упражнении 3.9 вам нужно только представить результаты теста 1% уровень значимости. Зачем? 1,29 1,21 1,00 0,79 0,71 100 студент 1 2 3 4 5 6 7 8 9 1 0 11 1 2 13 1 4 15 1 6 1 7 18 Указать на осмотр 30 29 дней 33 62 59 63 80 32 60 76 13 41 26 43 43 68 63 42 результат исследование.

Он не смог Пропустите Он не смог Пропустите Он не смог Пропустите Пропустите Он не смог Пропустите Пропустите Он не смог Пропустите Он не смог Пропустите Он не смог Пропустите Пропустите Он не смог студент 1 9 20 21 22 23 24 25 26 27 28 29 дней 30 31 32 33 34 35 36 Указать на осмотр 51 45 22 30 40 26 9 36 61 79 57 46 70 31 68 62 56 36 результат исследование Он не смог Он не смог Он не смог.

Пропустите Он не смог Он не смог Он не смог Пропустите Пропустите Он не смог Он не смог Пропустите Он не смог Пропустите Пропустите Пропустите Пропустите Пропустите 3,11. Предположим, вы проверили нулевую гипотезу на обоих уровнях. Ny значительный на 5% и 1%. При каких условиях вы представляете: 1) Только 1% результатов проверки.

2) Результаты теста уровня 5%. 3) Результаты на обоих уровнях значимости? 3.12. Формула регрессии между коммунальными платежами и (1) Личный доход и (2) упражнение 2.2 время в следующем формате (Стандартная ошибка показана в скобках): j> = ~ 27,6 + 0,178х; р = 48,9 + 4,84 *. (3,4) (0,004) (1,5) (0,10) Запустите r тест, чтобы проверить значимость коэффициентов Это необходимо. Четко выразить проверяемые нулевые гипотезы и их изменения Native.

Пожалуйста, объясните, почему вы сначала создаете ноль ги Thesis. 3,13. Выполните аналогичный тест G, чтобы увидеть коэффициенты регрессии. 101 Из оцениваемых в упражнениях 2.4 и 2.5 явно ноль Альтернативная гипотеза. 3,14. Согласно принятой гипотезе, 10% предельного дохода расы Иди к еде. Проверьте эту гипотезу, используя результаты оценки. Регрессия показана в уравнении (3.45).

Смотрите также:

Предмет эконометрика

Точность коэффициентов регрессии	Доверительные интервалы
Теорема Гаусса-Маркова	Односторонние t-тесты