Оглавление:





Точность коэффициентов регрессии
- Точность коэффициента регрессии Теперь рассмотрим теоретическую дисперсию оценок a и b. Он устанавливается следующим образом: Выражение воздушного шара (доказательство эквивалентного выражения Дж. Томас [найден в исследовании Томаса, 1983, раздел 8.3.3]: P ° p- ™ (a) = C1 + USCH и P ° p V a r W = ^ f e) — (3-25) Три очевидных вывода можно сделать из уравнения (3.25).
- Во-первых, чтобы Дисперсия a и b прямо пропорциональна дисперсии остаточного члена a2. Чем больше случайный коэффициент, тем хуже оценка. Wii. Это уже было объяснено в эксперименте Монте-Карло. В разделе 3.2. Серии II были намного менее точными, чем Серии I. Это произошло потому, что случайный член был удвоен в каждой выборке.
Удвоенное, стандартное отклонение удвоенное, удвоенное Стандартные отклонения А и В, во-вторых, чем больше наблюдений, Меньшая оценка отклонений. Людмила Фирмаль
Это также имеет несколько значений. большой Информация, которую вы имеете, ваши оценки могут быть более точными. В-третьих, чем больше дисперсия x, тем меньше дисперсия коэффициентов. Элемент регрессии. В чем причина этого? (1) Запомните коэффициент рег ресси рассчитывается исходя из наблюдаемого изменения у генерируется изменением х. (2) на самом деле Некоторые из-за изменений в x, а некоторые из-за изменений и.
Меньше дис Для Персии х относительное влияние факторов Высокая вероятность подростковой и ее регрессии при определении отклонения y Анализ Sion может быть неверным. На самом деле, В формуле (3.25) имеет значение не абсолютное, а относительное Маска а2 и вар (х). 83 На практике теоретическая дисперсия a или b не может быть рассчитана.
Вы можете получить оценку aw2, основанную на том, что GJ неизвестен, но остаточный. Очевидно, что распространение остатка к линии регрессии В общем, сузьте неизвестный разброс по линии y = a + px Остаток и случайный член для конкретного наблюдения не равны друг другу. Следовательно, выборочная дисперсия остаточного Var (e) равна Может быть использован для оценки A2. Я не могу Пожалуйста, задайте себе следующие вопросы, прежде чем продолжить.
Какая линия Это ближе к точке, которая представляет образец наблюдений для x и y. истинная линия >> = a + jlx или линия регрессии. )) = A + bx? Ответ: По определению он построен таким образом, чтобы линия регрессии Минимизируйте сумму квадратов расстояний между ним и значением Наблюдение. В результате остаточный спред в нем меньше, чем спред Значения and и Var (e) имеют тенденцию занижать оценку a2.
Конечно, мы можем Тем не менее, он показывает математическое ожидание Var (e). Зависимой переменной является [(n-2) / n] a2. Тем не менее, оп определить Си ^ = ^ V a r (*), (3,26) c $ 1 будет объективной оценкой c ^ (см. доказательство ниже) Работы Дж. Томаса). Уравнения (3.25) и (3.26) могут быть использованы для получения теоретических оценок. После извлечения дисперсии и квадратного корня из оценки a и b-оглушения Дарт отклонение.
Слишком громоздкий термин «вместо рейтинговых критериев» Отклонение функции плотности вероятности «коэффициент регрессии Используйте термин «стандартная ошибка» для коэффициента регрессии. В будущем про «п.» Поэтому для парного регрессионного анализа: \ sl L x s.o. (e) = p- * + 1 / / A и s.o. (A) = si qi + v * wj Hc- ° -w = fl ^ w (3.27) При оценке регрессии с помощью компьютерной программы:
- Стандартная ошибка рассчитывается автоматически одновременно Ками а и б. Результирующая связь объясняется в эксперименте выше Метод Монте-Карло, описанный в разделе 3.2. В серии I На основе случайных чисел, полученных от населения с нулевой средой И единица дисперсии (o2 = 1), х был набор чисел из 1 До 20 Var (x) легко вычисляется в 33.25. так 1 [, Ю., 52 pop.var (*) = -1 + ^ y = 0,2158 (3,28 Следовательно, истинное стандартное отклонение b составляет d / 0,001504 = = 0,039.
Какой результат получен компьютером вместо 10 опыта? Серия я? Он должен был рассчитать стандартную ошибку Изучение уравнения (3.27), эти результаты расчетов предыдущих 10 экспериментов Подать к столу. 3.5. Как видите, большинство оценок достаточно. Таблица 3.5 Эксперимент (б) Эксперимент (б) 1 0,043 6 0,044 2 0,041 7 0,039 3 0,038 8 0,040 4 0,035 9 0,033 5 0,027 1 0 0,033
Один основной момент должен быть подчеркнут. Людмила Фирмаль
Стандартная ошибка Общая оценка точности коэффициента регрессии. Она может Получить представление о кривых функции плотности вероятности Как показано на рисунке. 3.1. Но она не несет информацию Является ли оценка в центре распределения, Относительный, потому что он точен или находится в «конце» распределения Но неточно.
Очевидно, что чем больше дисперсия случайных членов, тем больше Боковая дисперсия остатка, и, следовательно, более важная стандартная ошибка Коэффициент уравнения регрессии, который допускает высокую вероятность Можно сделать вывод, что полученные коэффициенты неточны. Но это только Только вероятность.
По конкретному образцу Эффекты случайных коэффициентов в различных наблюдениях могут влиять друг на друга В долгосрочной перспективе коэффициент регрессии будет точным. Из этой проблемы Вообще говоря, я не могу сказать, произойдет ли это. упражнения Когда вам нужен конкретный результат игры Умения измеряются цифрами, повышая уровень игры, достигая определенного уровня Может быть представлен графически с использованием практики, так называемой Кривая обучения.
Это особенно актуально для видеоигр. В настоящее время он контролирует объекты, которые атакуют и защищают себя от других. Это объекты, управляемые программой. Те, кто участвует в первый раз 85 Вы обычно проигрываете через несколько секунд. Больше тебя Чем больше очков вы играете, тем быстрее вы привыкнете к игре Я приму это, Случайный коэффициент.
Предполагая количество очков Определяется по кривой обучения .y = 500 + 100x + s, Где у — результат следующей игры, а х — количество игр, в которые ранее играл игрок. Текущая игра (серийный номер текущей игры минус 1), случай Член чаепития. В следующей таблице приведены результаты первых 20 игр нового игрока. х автоматически изменяется с 0 на 19.
Взятый как ценность La получен с использованием случайного генератора с нормальным распределением Числа с нулевым средним и единицей дисперсии были сердцем в то время 400 оболочек; значение y и значение x С линейной кривой обучения. решение 1 2 3 4 5 6 7 8 9 10 X 0 1 2 3 4 5 6 7 8 9 и -236 -96 -332 12 -152 -876 412 96 1012 -52 в 264 504 368 812 +748 124 1512 1296 2312 1348 наблюдение 11 12 13 14 15 16 17 18 19 20 X 10 11 12 13 14 15 16 17 18 19 и 636 -368 -284 -100 676 60 8 -44 -364 -568 в 2136 1232 1416 1700 2576 2060 2108 2156 1936 2968
Оценка регрессии между y и x дает уравнение (в скобках Стандартная ошибка): у = 369 + 116,8 *. (190) (17,1) 3.1. Почему постоянный член этого уравнения не 500, а коэффициент Ent перед х не равен 100? 3.2. Что означает стандартная ошибка? 3.3. Эксперимент повторяется с 9 другими новыми игроками (в каждом случае.
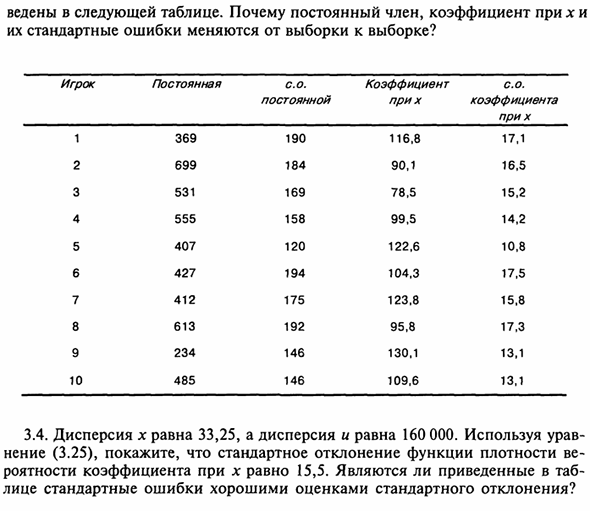
Случайные члены получаются путем умножения 20 различных наборов на 20 Случайные числа) и оценки регрессии для всех 10 игроков 86 Следующая таблица показывает. Почему постоянный член, коэффициент при х, Отличается ли стандартная ошибка от образца к образцу? Игрок 1 2 3 4 5 6 7 8 9 10 постоянная 369 699 531 555 407 427 412 613 234 485 A.
Определенная 190 184 169 158 120 194 175 192 146 146 коэффициент В х 116,8 90,1 78,5 99,5 122,6 104,3 123,8 95,8 130,1 109,6 A. коэффициент В х 17,1 16,5 15, 2 14,2 10.8 17,5 +15,8 +17,3 13,1 13,1 3.4. Дисперсия х равна 33,25, а дисперсия — 160 000. Операция (3.25), стандартное отклонение функции плотности Корневым фактором фактора х является 15,5. Есть ли вкладка Вы сталкиваетесь с хорошей оценкой стандартного отклонения стандартного отклонения?
Смотрите также:
| Предположения о случайном члене | Теорема Гаусса-Маркова |
| Несмещенность коэффициентов регрессии | Проверка гипотез, относящихся к коэффициентам регрессии |

