Оглавление:





Эксперимент по методу Монте-Карло
- Эксперимент Монте-Карло Я не знаю точно, кто экспериментировал с Луной Те Карло это так называется. Вероятно, это имя имеет некоторые Ношение знаменитого казино как символа случайного закона. Основная концепция объясняется аналогией. Предположим, что Свинья обучена находить трюфели.
- Это лесные грибы 74 (3.5) (3.6) Это считается деликатесом во Франции и Италии. Они дорогие Его трудно найти, и потому что это хорошая свинья, обученная находить трюфели. Это дорого. Проблема в том, как хорошо это понять Ня ищет трюфели. Она может время от времени находить их, но, вероятно, Она также пропускает много трюфелей.
В случае действия Что действительно интересно, так это выбор и заполнение земельных участков. Людмила Фирмаль
Отпусти трюфелей и поросят в некоторых местах и посмотри сколько грамм Она найдет Боба. С помощью таких контролируемых экспериментов вы можете: Непосредственно оцените степень успеха поиска. Какое это имеет отношение к регрессионному анализу? Проблема в том Не знаю истинного значения а и р (если нет, то почему Использовали ли вы регрессионный анализ для их оценки? ).
Поэтому мы не можем Например, хорошие или плохие оценки дают нам путь. Метод эксперимента Монте-Карло — эксперимент с искусственным контролем, Возможность такой проверки. Экспериментируйте как можно проще с методами У Монте-Карло есть три части. Прежде всего: 1) Выбраны истинные значения а и р. 2) Для каждого наблюдения выбирается значение x.
3) Процесс генерации случайных чисел (или ни одного) Случайное значение из таблицы случайных чисел) Случайный коэффициент и каждое наблюдаемое значение. Во-вторых, значение y генерируется для каждого наблюдения Существуют соотношения (3.1) и значения для a, p, x и u.
В-третьих, оцените параметры с помощью регрессионного анализа Откажитесь от a и b, используя только значения, полученные таким образом у и х данные. L и C и /) хороши в то же время вы можете увидеть Оцените а и р. Это позволяет почувствовать пригодность метода строительства. Регрессия. Первые два шага готовятся к применению регрессии Метод. Мы полностью контролируем модель, которую создаем, и знаем правду.
Различные значения для параметра. Это потому, что они решили сами. На третьем этапе Используйте метод, чтобы определить, может ли быть решена настроенная задача Вы можете получить хорошую оценку a и p, используя регрессию, т.е. Используйте только данные y и x. Причина проблемы заключается в следующем: Включите случайный фактор в процесс получения y.
Для т / фактор Если нет, то точка, соответствующая каждому наблюдению, Если вы точно нажмете строку (3.1), точные значения a и p Это просто определяется значениями у и х. Произвольно установите a = 2 и p = 0.5, чтобы истинная зависимость Дисплей: у = 2 + 0,5х + м (3,7) Для простоты предположим, что есть 20 наблюдений, и x принят Диапазон составляет 1-20.
Для случайных остаточных компонентов, Используйте случайные числа, полученные из нормально распределенной популяции Ноль со средним и единичной дисперсией нуля. Установить требуется Из 20 значений ga, …, ga20. Те случайные члены в первом наблюдении Дения просто равна TX и т. д. 75 Вы знаете значение chi и можете рассчитать значение y для каждого наблюдения. Используйте выражение (3.7).
- Это сделано в таблице. 3.1. При оценке рег сейчас Зависимость y от x: j> = 1,63 + 0,54l: (3.8) В этом случае оценочное значение a меньше (1,63) При a (2,00) b немного выше (J (0,54 по сравнению с 0,54)). Результат определялся совместным влиянием случайных членов в 20 наблюдениях. Очевидно, что в одном эксперименте такого типа Оценка качества регрессионного метода.
Повторите для дальнейшей проверки Эксперимент с тем же значением, что и истинное уравнение (3.7) х, но использовать новый случайный набор оставшихся терминов Такое же распределение (нулевое среднее и единичная дисперсия). Используя эти знаки Получить новый набор значений и значений x, y.
Он дал довольно хорошие результаты, Возможно, это просто счастливый случай. Людмила Фирмаль
Для экономии места таблица с новыми значениями и и y не указана. Вот результат оценки регрессии между новыми значениями y и x. >> = 2,52 + 0,48х. (3.9) Таблица 3.1 X 1 2 3 4 5 6 7 8 9 10 и -0,59 -0,24 -0,83 0,03 -0,38 -2,19 1,03 0,24 2, 53 -0,13 в 1,91 2,76 2,67 4,03 4,12 2,81 6,53 6,24 9,03 6,87 X 11 12 13 14 15 16 17 18 19 20 и 1,59 -0,92 -0,71 -0,25 1,69 0,15 0.02 -0,11 -0,91 1,42 в 9,09 7,08 7,79 8,75 11,19 10,15 10,52 10,89 10,59 13, 42 Второй эксперимент также был успешным.
Больше оказалось, b-немного меньше (3. Таблица 3.2 показывает 10-кратное оценочное значение b Повторите эксперимент, используя разные наборы случайных ци Сел в каждой версии. может Однако в некоторых случаях оценочное значение Недооцененные значения и другие завышенные значения.
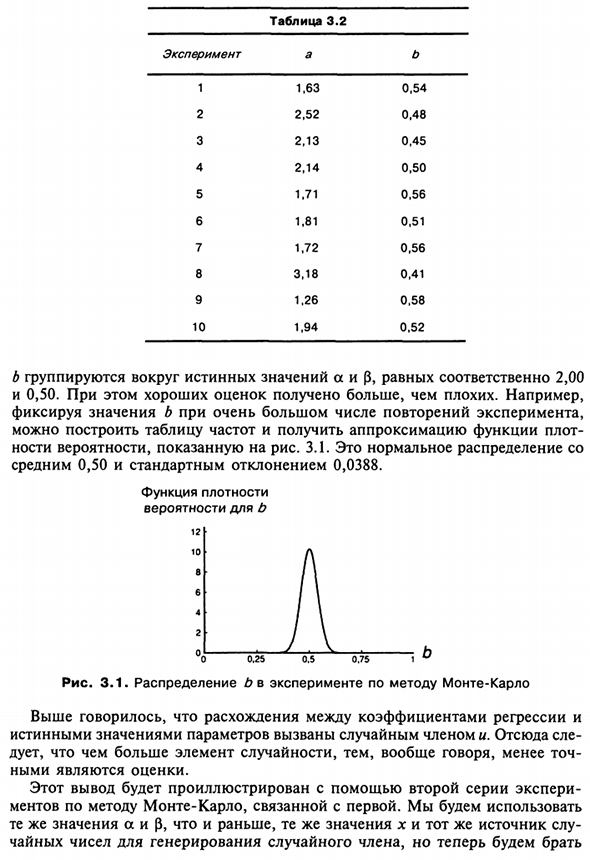
В общем, значения a и b группируются вокруг истинных значений a и p, равных 2,00 соответственно. И 0,50. В то же время, была получена лучшая оценка, чем плохая. Например Изменить значение b в большом количестве итераций, Создайте таблицу частот, чтобы получить приближение функции плота Вероятность 3.1 показана на рисунке.
Это нормальное распределение Среднее 0,50 и стандартное отклонение 0,0388. Функция плотности вероятность б 12 1 0 8 6 4 2 «Около 0,25 0,5 0,75 1 ^ Рисунок 3.1. Распределение b в эксперименте Монте-Карло. Как указано выше, коэффициент регрессии и Истинные значения параметров обусловлены случайными условиями. Отсюда Чем больше коэффициент случайности, тем меньше точность. Оценка важна. Этот вывод будет объяснен с использованием второй серии экспериментов.
Первый связанный офицер полиции Монте-Карло. использование То же значение a и p, то же значение x и тот же источник, что и раньше Номер тройника для генерации случайных терминов, но теперь мы берем 77 Таблица 3.3 X 1 2 3 4 5 6 7 8 9 10 И -1,18 -0,48 -1,66 0,06 -0,76 -4,38 2,06 0,48 5,06 -0,26 в 1,32 2, 52 1,84 3,94 3,74 0,62 7,56 6,48 11,56 6,74 X 11 12 13 14 15 16 17 18 19 20 И 3,18 -1,84 -1,42 -0,50 3,38 0,30 0.04 -0,22 -1,82 2,84 в 10,68 6,16 7,08 8,50 12,88 10,30 10,54 10,78 9,68 14,84
Случайное значение термина для каждого наблюдения. Последний является * / ‘, (/ = 1, 2, …, n), значение которого равно двойному случайному числу: И \ = 2м {, …, и 20 = 2rn20. На самом деле, используйте точно такой же выбор Случайное число такое же, как и раньше, но на этот раз значение удваивается. Давай На основании данных таблицы. 3.1.
Рассчитать таблицу. 3.3. Далее оцените регрессию между Получите уравнение для y и x: ? = 1,26 + 0,58 *. (3.10) Это уравнение намного менее точно, чем уравнение (3.8). Таблица 3.4 Эксперимент а б 1 1,26 0,58 2 3,05 0,45 3 2,26 0,39 4 2,28 0,50 5 1,42 0,61 6 1,61 0,52 7 1,44 0,63 8 4,37 0,33 9 0,52 0,65 1 0 1,88 0,55 78 В таблице. 3.4 показаны результаты всех 10 экспериментов с u ‘= 2m.
Назовите это Experiment Series II, оригинальная серия экспериментов Сотрудники милиции, результаты приведены в таблице. 3.2, серия I. При сравнении Tab. В 3.2 и 3.4 значения a и b во второй таблице Они еще не систематизированы, но довольно нестабильны Склонность недооценивать или переоценивать оценки.
Детальное расследование выявило важные особенности. Серия I Значение b в эксперименте 1 составляет 0,54. 0,04. В серии II значение b в эксперименте 1 составляет 0,58, что является завышением состава Это было 0,08. Это вдвое больше, чем раньше. Повторите то же самое Каждый из остальных девяти экспериментов и рег Ressii для каждого эксперимента.
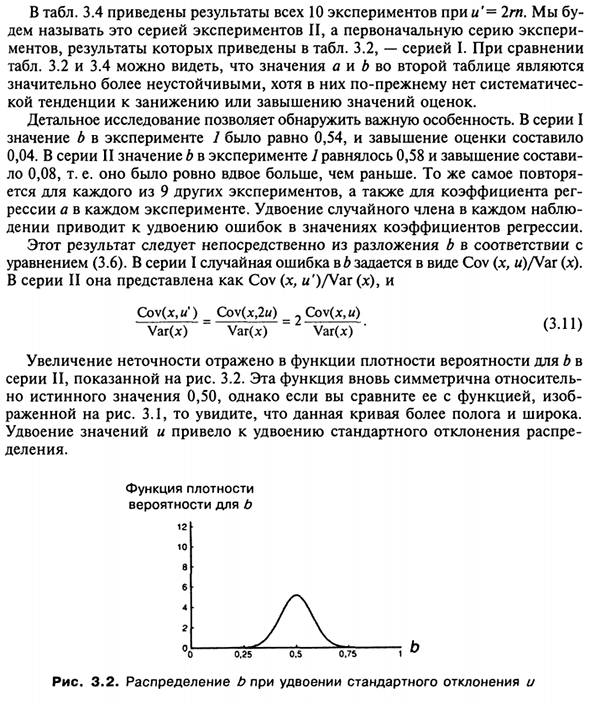
Двойные случайные члены в каждом наблюдателе Разведение удвоит значение коэффициента регрессии. Результат В уравнении (3.6) Series I случайная ошибка b задается в виде Cov (x, w) / Var (x). В серии II это выражается как Cov (x, w ‘) / Var (JC). SOU (X, C) = Cov (x, 2u) = Cov (x, u) Var (x) Var (x) Var (x) ‘(ZL1> Увеличение неточности отражается в функции плотности вероятности b. Серия II 3.2 показана на рисунке 2. Эта функция снова симметрична.
Но истинное значение составляет 0,50, но по сравнению с функцией, Показано на рисунке. 3.1 видно, что эта кривая более плоская и широкая. Удвойте значение и удвойте стандартное отклонение распределения Департамент. Функция плотности вероятность б 12 | — 1 0 б 4 2 О л «х. Р — ^ — ^ — £ \ b 0,25 0,5 0,75 Рисунок 3.2. Распределение b, когда стандартное отклонение удваивается
Смотрите также:
| Качество оценки: коэффициент R2 | Предположения о случайном члене |
| Случайные составляющие коэффициентов регрессии | Несмещенность коэффициентов регрессии |

