Регрессия по методы наименьших квадратов

Регрессия по методы наименьших квадратов

• Регрессия наименьших квадратов Предположим, что четыре наблюдения хны отображаются Рисунок 2.1, и задание для вас установлено — определите значения уравнений a и J} Соотношение (2.1). В грубом приближении, чтобы сделать это: Построение линии, которая наиболее близко соответствует четырем точкам P К этим точкам.

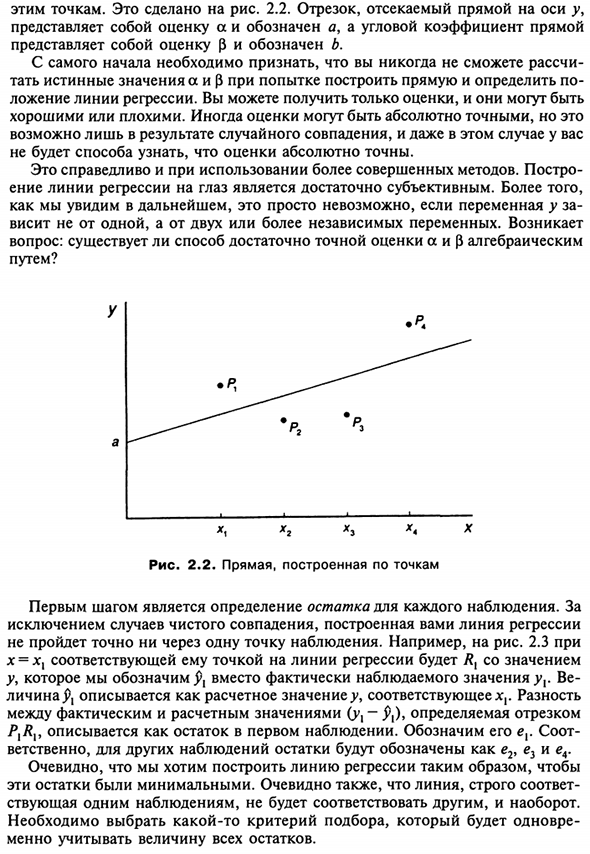
• Это сделано на рисунке. 2.2. отрезок отрезан прямой линией на оси у, Представляет оценку a, представленную q, и наклон линии Представляет оценку (обозначенную $ и b). С самого начала вы должны признать, что вы не можете рассчитать Растопить истинное значение а и р при попытке создать прямую линию, Прокладка линии регрессии. Это хорошо или плохо?

Только оценки могут быть получены. Людмила Фирмаль

Оценка может быть абсолютно точной, Возможно только в результате совпадения, даже в этом случае Нет никакого способа узнать, что оценка является абсолютно точной. Это также верно при использовании более продвинутых методов. Для конструкции Линия регрессии глаз очень субъективна. Кроме того, Как вы увидите позже, переменная Зависает от двух или более независимых переменных вместо одной.

Вопрос: а (3 алгебраический В? • 1 Рисунок 2.2. Точка построения линии Первым шагом является определение остальной части каждого наблюдения. для Построена линия регрессии, за исключением случая чистого совпадения Не проходит через одну точку наблюдения.

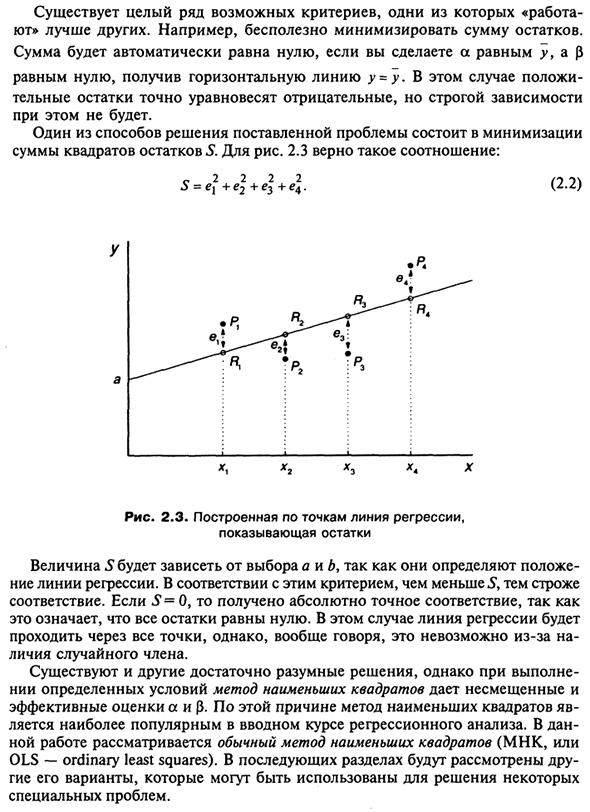
Например, на рисунке 2.3 х = х Соответствующая точка на линии регрессии х имеет значение R { у, это вместо фактически наблюдаемого значения р {ув Символ ^ записывается как вычисленное значение >>, соответствующее x. разница Между фактическим значением, определенным сегментом, и расчетным значением (y {-j ) P {R {, написано как остальная часть первого наблюдения.

Представлено е. {. соответствующий Таким образом, в других наблюдениях остатки показаны как e2, e3 и sp. Очевидно, что создание линии регрессии Эти остатки были минимальными. Кроме того, линия Это согласуется с некоторыми наблюдениями, а не с другими наблюдениями. Обратное также верно. Необходимо выбрать критерии выбора для одновременного Рассмотрим все значения остатков.

• Существует множество возможных критериев, одним из которых является «работа». да лучше других. Например, минимизация суммы баланса не имеет смысла. Если он равен y, сумма автоматически равна нулю и (3 Получает горизонтальную линию y = y, равную нулю. В этом случае Твердые остатки сбалансированы точно с отрицательными, но серьезными зависимостями Не так.

Одним из способов решения этой проблемы является минимизация Сумма квадратов S невязок. 2.3 Следующее соотношение верно: с 2 2 2 2 (2.2) Рисунок 2.3. Пунктирная линия регрессии, Показать остатки Значение S зависит от выбора a и b. Линия регрессии.

Согласно этому стандарту, менее 5, более строгий Соответствие. Людмила Фирмаль

Если S = ​​0, получается абсолютно точный ответ. Это означает, что все остатки равны нулю. В этом случае линия регрессии Проходит все точки, но, вообще говоря, это невозможно Случайная членская лицензия. Однако есть и другие достаточно разумные решения. При определенных условиях метод наименьших квадратов беспристрастен, Эффективная оценка а и р.

По этой причине наименьшие квадраты явные Является самым популярным вводным курсом по регрессионному анализу. В дан В этой статье обычный метод наименьших квадратов (OLS или МНК-нормальные наименьшие квадраты). В следующем разделе другой Варианты, доступные для некоторых решений Специальный выпуск 5

Смотрите также:

Предмет эконометрика

Коэффициент частной корреляции	Регрессия по методу наименьших квадратов: два примера
Модель парной линейной регрессии	Детальное рассмотрение остатков