Оглавление:



Модель парной линейной регрессии
- Модель парной линейной регрессии Коэффициент корреляции показывает, что две переменные связаны друг с другом. С другом, но он не дает представления о том, как они связаны Us. Рассмотрим случай, который мы предполагаем, более подробно. Одна переменная зависит от другой переменной. Не ожидайте получить точное соотношение сразу Исключая их, между любыми двумя экономическими показателями Если присутствует по определению.
- Учебники по экономике Теоретически эта проблема обычно решается путем уменьшения соотношения Это точно и предупреждает читателя, что это приближение Вы. Однако в статистическом анализе корреляция Получается путем явного включения случайного коэффициента, описываемого Остальные участники чаепития. Давайте посмотрим на простейшую модель. >> = cx + px + и. (2.1) Величина y, рассматриваемая как зависимая переменная, равна 2 Настройки: 1) Неслучайный компонент a + px, где x служит объяснением.
Является ли вычитающей (или независимой) переменной, а значения констант a и p похожи на pa. Людмила Фирмаль
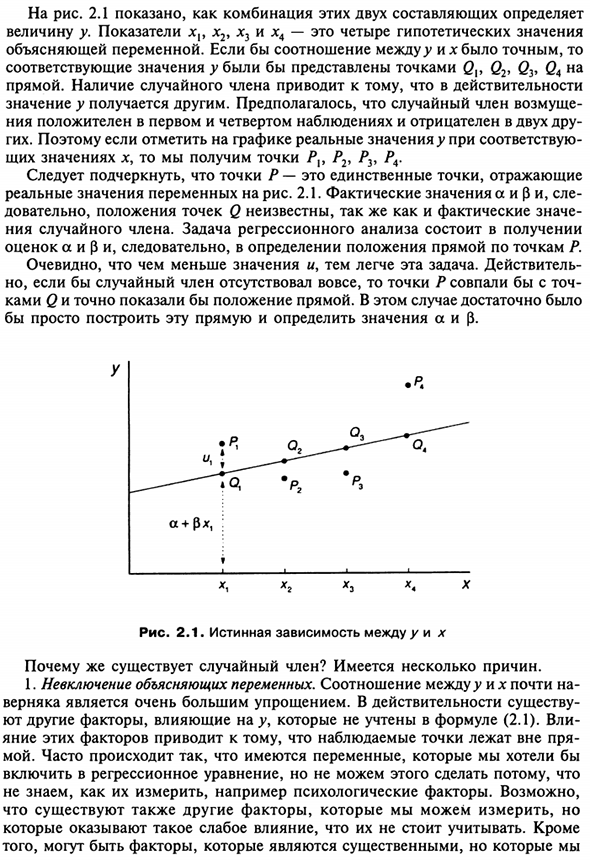
Размерность уравнения; 2) Случайные члены. 53 На рисунке 2.1 показано, как комбинация этих двух компонентов определяет значение у Показатель x {9 x2, x3 и x4 — 4 виртуальных значения Пояснительная переменная. Если соотношение между у и х является правильным, Соответствующее значение у представлено верхними точками Qv Q2, Q3, Q4. Непосредственно.
Существование случайных терминов на самом деле Значение у отличается. Случайный член считался возмущенным Положительно для первого и четвертого наблюдений, отрицательно для двух других наблюдений Муравьиная. Следовательно, соответствует фактическому значению >> на графике Получите значение х, точки P {, P2, P2, P4. Следует подчеркнуть, что точка P является единственной точкой, которая отражает Фактическое значение переменной figure.
2.1. а и (3 и В результате местоположение и фактическое значение точки Q неизвестны. Случайные участники. Задача регрессионного анализа — получить оценка a и p и, следовательно, положение линии в точке P Очевидно, что чем меньше значение, тем проще эта задача. эффективным Но если нет случайных членов, точка P Ками Q и определенно покажет линию позиции.
- В этом случае этого было достаточно Создайте эту строку а и (3. Рисунок 2 1. Истинные отношения между у и х Почему есть случайные участники? Есть несколько причин. 1. Не включайте пояснительные переменные. Отношения между Y и JC почти Конечно, очень большое упрощение. В реальности Существуют и другие факторы, влияющие на y, которые не учитываются в уравнении (2.1).
ВЛИ Определение этих факторов приводит к тому, что наблюдаемые точки находятся непосредственно вне Часто случается, что есть переменные, которые мы хотим Включить его в уравнение регрессии, но это невозможно. Я не знаю, как их измерить, например, психологические факторы.
Вероятно Что есть другие элементы, которые можно измерить. Людмила Фирмаль
Они имеют слабые последствия, которые не следует принимать во внимание. за исключением той Там могут быть важные факторы, но мы 54 Из-за недостатка опыта такие вещи не рассматриваются. Объедините все это В общем, получите то, что указано как и. Если вы точно знаете Здесь есть переменные, и мы смогли их точно измерить.
Вы можете включить их в уравнение и исключить соответствующие элементы Из случайных членов. Проблема в том, что мы никогда То, что включено и не включено в эту популяцию, определенно. 2. Агрегация переменных. Во многих случаях зависимость рассматривается Мост — это попытка соединить многие микроэкономики Соотношение.
Например, функция общего потребления Пытки всего общего выражения индивидуальных решений по расе Это движется. Поскольку отдельные отношения, вероятно, имеют разные параметры, Попытки определить отношение к общей стоимости Доход это только оценка. Расхождения наблюдаются с этим Из-за наличия случайных членов. 3.
Неверное описание структуры модели. Структура модели Неправильно или неправильно вообще. Вот ты где Много возможных примеров. Если отношение ссылается на данные времени В серии значение у не является фактическим значением JC, Ожидаемое значение за предыдущий период.
Ожидаемые факты Если значения тесно связаны, между ними Это зависимость, но это только приближение, и расхождение снова Это потому, что есть случайные члены. 4. Функциональные характеристики не верны. Соотношение функций Между y и x можно определить математически неправильно. Например Истинные зависимости могут быть не линейными, но более сложными Th.
Не имею Линейные отношения описаны в главе 4. Конечно же Используйте правильную математику, чтобы избежать этой проблемы Формула, но любая из самых сложных формул близка Существующие расхождения влияют на оставшийся период. 5. Ошибка измерения.
Для одного или нескольких взаимосвязанных размеров Наблюдения не совпадают, если в переменной есть ошибка Корреляция и существующие расхождения способствуют Оставшийся член. Остаточный термин является собирательным выражением всех этих факторов. Болит Если вы заинтересованы только в измерении влияния х на у, Если не осталось членов, это намного удобнее.
Если он этого не сделал Тогда вы можете узнать изменение у от наблюдения к наблюдению. Это было вызвано изменением х и смог точно рассчитать р. Но в действии Каждое изменение у частично вызвано изменением и. Жизнь становится трудной. По этой причине его иногда называют шумом.
Смотрите также:
| Почему ковариация не является хорошей мерой связи | Регрессия по методы наименьших квадратов |
| Коэффициент частной корреляции | Регрессия по методу наименьших квадратов: два примера |

